PHZ3400-09 Modern Physics

“ Ah, the reason we all majored in physics in the first place... ”

Group 3 is the best

Modern Physics Society of Physics Students Atomic Structure Physics Relativity Quantum Mechanics Structure of Matter Century 20th - 21st Giants Einstein

Modern Physics (Greek: physis – φύσις meaning "nature") refers to the branches of physics developed from the discovery of the quantum nature of physics at the beginning of the 20th century. More generally, the term can refer to any branch of physics developed from this time period onward.

Modern Physics introduces the exciting developments of physics in the 20th Century (and some of the 21st). Well, anything that happened after PHY2049. We will see how the seeds of this great revolution were planted in the greatest triumph of the 19th century physics! And a revolution it was! There is no other way to describe the fascinating, surprising, and mind boggling discoveries of relativity, quantum mechanics, and the structure of matter. Some of the great scientists we will encounter along the way are Planck, Einstein, Curie, Rutherford, Bohr, Pauli, Dirac, Schrodinger, Heisenburg, Fermi, Geynman, Rydberg, and Schrieffer. Two of these giants of the 20th century physics, Dirac and Schrieffer, have served on the FSU faculty!

Introduction

• Notes: Lecture
• Lecturer: Dr. Vlad's Friend
• Time: 12:20pm - 1:10pm
• Dates: Wednesday, January 14, 2009 & Friday, January 16, 2009
• Place: The Classroom Building, HCB 317, Florida State University

“ At the end of the 19th century, scientists had gotten quite a lot done. But there was no explanation for things that happened at the quantum level. What happened when things got very small and very fast? ”

Black Body Radiation

Intensity vs. Wavelength

One of the mysteries that led to a break through in modern physics, was that of thermal radiation. Thermal Radiation is electromagnetic radiation that is emitted by all objects merely because of their temperature. The classical wave picture of electromagnetic radiation failed to explain phenomenon. Early observations found that the total intensity radiated over all wavelengths increases as the temperature increases. Careful measurements found that the total intensity in creases as the fourth power of the temperature:

$I=\sigma T^{4}\!$

This equation is known as Stefan's Law, where $\sigma$ is known as the Stefan-Boltzmann constant.

A second observation made was that the wavelength at which the radiancy reaches a maximum value decreases as the temperature is increased, in inverse proportion to the temperature. Careful observations determined that the proportionality constant, such that:

$\lambda _{max}T=2.898x10^{-3}m\cdot K\!$

This equation is known as Wien's displacement law.

Since the amount of radiation emitted by a solid object depends not only on the temperature, but also on other factors, such as the properties of the surface, physicists simplified the problem by considering an object whose surface is completely black, or a blackbody. Using this simplification physicists were able to ignore any radiation being reflected from the surface of the object.

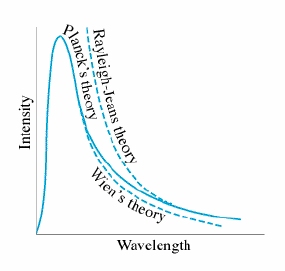
The closest classical physics came to describing blackbody radiation was the Rayleigh-James formula, which was based firmly on the classical theories of electromagnetism and thermodynamics.

$R(\lambda )={\frac {8\pi }{\lambda ^{4}}}kT{\frac {c}{4}}\!$

However, this was only able to predict radiance at high wavelengths compared against observations (as seen in the graph). The failure of the Rayleigh-James formula and thereby the failure of classical physics to explain blackbody radiation is known as the ultraviolet catastrophe.

Planck's Hypothesis

Max Planck

The new physics that gave the correct interpretation of thermal radiancy was proposed by the German physicist Max Planck in 1900. Planck needed to reduce the radiance at short wavelengths, to correct the Rayleigh-James model. To do this he suggested that an oscillating atom can absorb or re-emit energy only in discrete bundles, or quanta. If the energy of the quanta were proportional to the frequency of the radiation, then as the frequencies became large, the energy would similarly become large; since no individual wave could contain more than $kT$ (the mean total energy of an oscillating atom) of energy, no standing wave could exist whose energy quantum was larger than $kT$. This effectively limited the high-frequency (low-wavelength) radiant intensity, and solved the ultraviolet catastrophe. In Planck's theory, each oscillator can emit or absorb energy only in quantities that are integer multiples of a certain basic quantity of energy $\epsilon$,

$E=n\epsilon \!$

where n takes on a positive integer value. Furthermore, the energy of each of the quanta is determined by the frequency

$\epsilon =h\nu \!$

where $h$ is Planck's constant. Based on this assumption, Planck calculated the radiancy to be

$R(\lambda )=({\frac {c}{4}})({\frac {8\pi }{\lambda ^{4}}})[({\frac {hc}{\lambda }}){\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}]\!$

Specific Heat of Solids

• ${C_{v}}/{N_{A}}=const.$
• Cv = 3 Na K from classical physics
• But at low temperatures C drops sharply and approaches zero
• Phonons: quantization of lattice vibrations

Photoelectric Effect

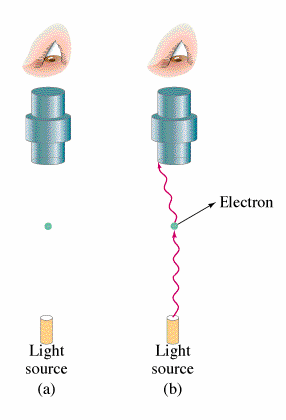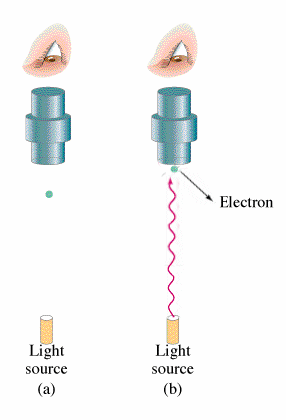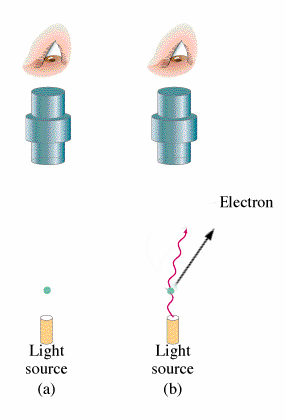
If Nobel prizes were given on the basis of popularity of the work alone then it would make no sense as to why Einstein won the Nobel prize for the Photoelectric Effect but not for his work on general relativity. The photoelectric effect does however have huge implications for modern physics and provides insight into the principles of Quantum Mechanics.

What is observed experimentally when electromagnetic radiation strikes the surface of a metal is that the electrons are emitted. This occurrence is what is known as the Photoelectric Effect. The energy of these electrons can be determined by adding a electrical potential. As one increments the voltage higher and higher one will find a voltage where no more electrons will reach the other plate. From this voltage one can find the kinetic energy of the electrons. Classical theory leads to the belief that both the intensity of the light and the frequency of the light will increase the energy of the ejected electrons. However, the kinetic energy of the electrons emitted does not depend on the intensity of the beam but rather it increases linearly with the frequency of the light. Increasing the intensity of the beam will increase the number of electrons emitted but not their energies. Depending on the type of the metal, there will be a minimum frequency for which and electron will be emitted. The following equation summarizes this:

$hv=\phi +E_{k_{max}}\,$

where phi is the binding energy of the metal, h is planck's constant, and v is the frequency.

All of this is significant because in classical theory there should be no threshold for electron emissions.

Side Note: Red light emits no electrons regardless of intensity.

Particle-Wave Duality and de Broglie Wavelength

Einstein proposed, in explaining the photoelectric effect, that light was not continuous, but that it was delivered in packets, known as photons. However this hypothesis failed to explain Young's Double Slit Experiment, in which light displayed wave-like properties (interference and diffraction). This led to the reasoning that light is not either particles or waves; it is somehow both particles and waves.

Louis de Broglie

This wave-particle duality of light led the French physicist Louis de Broglie to pose a question about particle-wave duality. Was this phenomenon only a property of light or is property of material objects as well? De Broglie suggested, lacking any experimental evidence in support of his hypothesis, that associated with any material particle moving with momentum $p$ there is a wavelength $\lambda$ related to $p$ according to

$\lambda ={\frac {h}{p}}\!$

The wavelength $\lambda$ of a particle computed according to this equation is called its de Broglie wavelength.

• Davidsson Germer experiment
• Thompson Reid experiment

Uncertainty Principle

Classical Wave Uncertainty

This uncertainty relationship stems from the difficulty in determining the position and wavelength of a classical wave simultaneously. Consider a sine wave. A sine wave repeats endlessly from $x=-\infty$ to $x=\infty$. If you were to ask "Where is the wave located?" you would not be able to provide an answer since it is everywhere. However, if you add another wave of different wavelength you will begin to get a beat pattern, with periods of higher and lower amplitudes.

Heisenberg Uncertainty Principle

• Measurement always disturbs object

• Deterministric view of nature is fundamentally flawed

You cannot know both position and momentum simultaneously

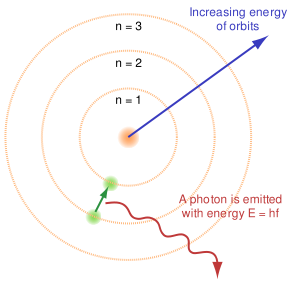
Atomic Spectra

The atomic line spectra is the phenomena where photons are absorbed and emitted by atoms at characteristic frequencies. Classically, according to the Lorentz theory, an electron in orbit around a nucleus is accelerated, causing it to emit electromagnetic radiation. This must be accompanied by a decrease in kinetic energy of the electron, causing it to spiral into the nucleus and become unstable. This is not what happens however as the electrons can only orbit around the nucleus in specified orbits with defined energies. The energies at each level are given by:

$E=-hR/n^{2}$

Bohr's model of an atom

• Spectra Lines and Atomic Spectra
• Plum Pudding model of atom
• Rutherford's scattering experiment
• Planetary model contradicts experiments

1. Stability of matter
2. Atomic Spectra lines

• Bohr's Model 1913 basic hypothesis

1. Electrons in atoms follow classical physics and Rutherford's atomic model
2. An electron jumping the specified orbital levels will either emit or absorb electromagnetic radiation
3. This was great for explaining the Rydberg formula for the emission of spectral lines

• Bohr's theory applied to hydrogen like atoms

1. It was a much simplified version of the actual atom, and could not be applied to larger atoms

• Line Spectra (Rydberg's formula)

${\frac {1}{\lambda _{\mathrm {vac} }}}=R_{\mathrm {H} }\left({\frac {1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right)$

Atomic Shell Structure

• quantum numbers (principal, orbital, magnetic, spin)
• Selection rule in quantum transitions N = +- 1
• Electron configurations
• Pauli exclusion principle
• Periodic table

Schrödinger Equation

Erwin Schrodinger

For 1 particle in 3D, the time-dependent Schrödinger Equation is as follows

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,\,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,\,t)$

where

• $\mathbf {r} =(x,y,z)$ is the particle's position in three-dimensional space,
• $\Psi (\mathbf {r} ,t)$ is the wavefunction, which is the amplitude for the particle to have a given position r at any given time t.
• $m$ is the mass of the particle.
• $V(\mathbf {r} )$ is the potential energy of the particle at each position r.

This describes many things but not waves at a very high energy, and as such further relativistic derivations were reconciled by Dirac and others later in the 20th century.

Sources

• Description of Modern Physics - Real Wikipedia & Syllabus written by Ingo Wiedenhover
• Krane, Kenneth Modern Physics