6th Week: The Early Universe and Big Bang Nucleosynthesis
The Big Bang Cosmology
Cosmological principle
The cosmological principle, which is the more general version of the Copernican principle, states that on large spatial scales, the Universe is homogeneous and isotropic. This means that there is no special point in the Universe. Homogeneity of the universe means that the universe has the same property at any regions from point to point. Isotropy of the universe means that the universe looks the same from all directions. We know that at small scales the universe is not homogenous and not isotropic otherwise any structures e.g. galaxies, stars, planets and humans would not even exist. However provided that we consider the universe on average on large scales, it looks approximately homogenous and isotropic. The observed cosmological scales are therefore approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 500} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mpc} in which the cosmological principle works.
The expanding Universe
Before 1915, it was believed that the cosmos was static and infinite. But the infinite Universe (Newtonian Universe) was ruled out soon due to the Olbers paradox, that states for such a Universe the dark night should not exist. The Einsteins theory of gravitation suggested that the Universe is no more static. But however in order to get a static Universe solution Einstein added a so called cosmological constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} which later he called it his greatest blunder. In 1922 Friedmann solved the Einsteins equations for isotropic and homogeneous universe and found that the Universe is either expanding or collapsing. This was experimentally discovered by Hubble in 1928, that the Universe is expanding and the expansion law is the following
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} = H_0 \vec{R} \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} is the so called Hubble constant, which is today believed to be
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0 = 70.1 \pm 1.3 \quad (km/s)/Mpc \ . }
The Hubble "constant" is not a constant, but is actually a time varying quantity. Defining a scale factor, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R} = a \vec{x} \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} is the comoving coordinate, one can find the folowing relation
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \frac{\dot{a}}{a} \ . }
Friedmann equations
From the large-scale distribution of galaxies and the near-uniformity of the CMB temperature, we have good evidence that the universe is nearly homogeneous and isotropic. Under this assumption, the space-time metric can be written in the form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ds^2 = -c^2dt^2 + \frac{\mathrm{d}r^2}{1-k r^2} + r^2 \mathrm{d}\mathbf{\Omega}^2 \ , }
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{d}\mathbf{\Omega}^2 = \mathrm{d}\theta^2 + \sin^2 \theta \, \mathrm{d}\phi^2 \ . }
There are two independent Friedmann equations for modeling a homogeneous, isotropic universe. They are:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3} \rho - \frac{kc^2}{a^2} + \frac{\Lambda c^2}{3}}
which is derived from the 00 component of Einstein's field equations, and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{H} + H^2 = \frac{\ddot{a}}{a} = -\frac{4 \pi G}{3}\left(\rho+\frac{3p}{c^2}\right) + \frac{\Lambda c^2}{3}}
which is derived from the trace of Einstein's field equations.
Using the first equation, the second equation can be re-expressed as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\rho} = -3 H \left(\rho + \frac{p}{c^2}\right) \ , }
which eliminates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda \!} and expresses the conservation of mass-energy.
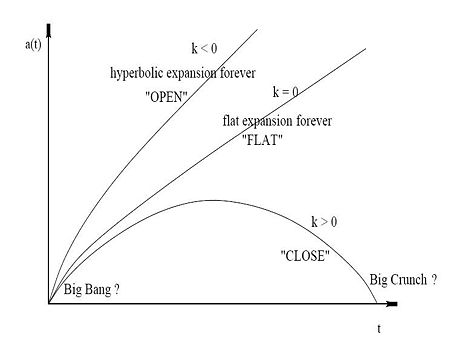
If the scale factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is taken to be 1 at the present time, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} describes the spatial curvature when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 1} (i.e. today). If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is positive, then the Universe is geometrically viewed as a hyperspherical, or also called as a closed Universe. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is zero, then the universe is flat. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is negative, then the universe is hyperbolic in geometry and also called an open Universe. In the closed Universe the expansion stops at some point and then recollapses to a Big Crunch. The flat Universe expands forever. The open Universe expands with acceleration and the end result is known as Big Chill.
Solution of the Friedmann equations
For simplicity, from now on we work in the units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1} . Then the fluid equation is just
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\rho} = -3 H \left(\rho + p\right) \ . }
The equation of state generally can be written as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = w \rho \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=0} for cosmological dust, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=1/3} for radiation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=-1} for cosmological constant or vacuum energy. The general solution is then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho =\rho_0 \left(\frac{a}{a_0}\right)^{-3(1+w)} \ . }
And the solution to the Friedmann equation gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a =a_0 \left(\frac{t}{t_0}\right)^{2/[3(1+w)]} \ . }
Evolution of density with time
Putting the las two equations together we obtain
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(t) = \rho_0 \left(\frac{t}{t_0}\right)^{-2} \ , }
where the subscript Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} denotes as the quantity for today. Thus, the density evolves the same regardless of the type of the fluid. Further substitution defines the Hubble constant in terms of time
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(t) = \left(\frac{2}{3(1+w)}\right)\frac{1}{t} \ . }
Relying on the observation of Hubble constant and using the equation of state parameter one can find the approximate age of the Universe. For a dust-filled Universe this time is equal to
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0 = \frac{2}{3H_0} \approx 9.2 \times 10^9 \quad years \ . }
Early Universe
Freeze -out time
weak reactions eventually end reacting slower than the cooling time of the