Geometrically Frustrated Materials

The main focus of solid state physics is on macroscopic properties of solid materials that result from interactions between atoms. Solid state physics is extremely interested in how these interaction come to an equilibrium to order in a certain way such as antiferromagnetism. One emergent property is disorder that arises from geometric frustration and this is the subject of much perplexing research because there seems to be no equilibrium between interactions or no unique ordering state.

What is geometric frustration?

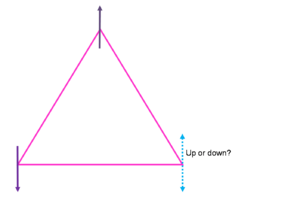
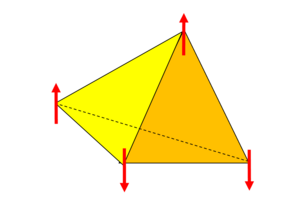
Frustration is the inability of a material to find a single ground state and instead has a highly degenerate ground state. The reason for this is because the geometry of the crystal is such that any arrangement of its constituent parts on the lattice cannot simultaneously satisfy all interactions. Most of the time this is referring to spins on a lattice in which the magnetic ordering is the subject of interest but this may also refer to the arrangement of oxygen and hydrogen atoms in water ice. In one dimension, consider a triangle with a spin on each vertex (see Fig.1). Two spins are satisfied and one spin is frustrated. That is, one spin can align up or down to satisfy a specific interaction but cannot satisfy all interactions. In three dimensions consider a tetrahedral where there is no possible configuration of four Ising spins on the vertices where they will all align antiferromagnetically (see Fig. 2). Both of these cases have competing interactions between the order of the lattice imposed on the local moments and the interactions between the moment themselves.

The size of the frustration parameter $f$, defined by the ratio of the Curie-Weiss temperature and the expected mean field ordering temperature (Néel or Curie temperature) or ${\frac {\theta _{CW}}{T_{N}}}$, is used to determine the extent of the frustration in a material. If $f<10$, then the material is said to be frustrated.

Figure 1. The configuration of spins on a triangle does not allow for all interaction to be satisfied. The left most spin can align up or down to compensate for its neighbor to the right or left but it cannot compensate for both spins at the same time

.

Figure 2. Four Ising spins on a tetrahedral lattice. Not all spins can align antiferromagnetically because they are arranged on the vertices of a tetehedra. The bottom right most spin interaction is satisfied but not the left most spin interaction.

.

Degenerate ground states means that instead of a ground state characterized by a single potential like in a ferromagnet, it is composed of many potential wells of various depths and this is though to lead to the strange properties exhibited by these materials.

Water Ice

Water ice was the first geometrically frustrated material to be studied. In 1936 Giaugue and Stout published The Entropy of Water and the Third Law of Thermodynamics where they reported that water ice has a residual entropy of 185.3 J/(mol•K). To find this, they first measured the heat capacity of water from the liquid through the ice state in a calorimetry experiment. Then they integrated the results and added in the contributions from latent heat to find the entropy. The entropy in the limit of 0 K was found by extrapolating the low temperature values to 0 K.

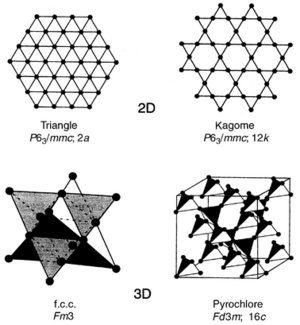
Types of Frustrated Lattices

Each of these crystal lattices are composed of a pattern of triangles and this is the crux of the frustration. Materials that are most likely to exhibit geometric frustration have a triangle based lattice and have short-range antiferromagnetic ordering.

Figure 3. These lattices are all composed of triangles with spins located at the black dots. Because of the structure, these lattices are frustrated when nearest neighbor antiferromagnetic interactions are present.

.

Triangle

There exisits a unique ground state called the Failed to parse (unknown function "\degrees"): {\displaystyle 120\degrees} state.

Kagome

The name of the Kagome lattice is derived from a Japanese basket-weaving pattern because of their similarities. The crystal structure is characterized by an corner-sharing, overlapping triangle pattern. There is no unique ground state for this lattice.

Pryochlore

The pryochlores are of the chemical form $A_{2}B_{2}O_{7}$ where the electronic spins are on the A-sites. Usually the A site is filled by a rare earth ion and the B site is filled by a transition metal. The crystal structure is characterized by a corner-sharing tetrahedral pattern.

Characterization

To experimentally study frustrated systems, one looks for singularities or critical temperatures in such bulk probes as heat capacity and magnetic susceptibility. The Heat capacity of a material is useful because from that entropy can be easily calculated and entropy is a gauge of the disorder in a system. It is interesting to know how to entropy approaches zero in the limit of 0 K because from that information on how the system orders is gained. According to the Third Law of Thermodynamics, entropy is zero at zero Kelvin, but as mentioned for water ice, in frustrated systems the entropy tends to a finite value in the limit of zero Kevin. This is a common characteristic of geometrically frustrated materials and is thought to arise from the fact that there exists degenerate ground states.

Another characteristic of frustration is the inverse of the magnetic susceptibility curve. In antiferromagneitc nonfrustrated systems the ordering temperature $T_{N}=\theta _{CW}$ where for antiferromagnetic frustrated systems $T_{N}<<\theta _{CW}$ (See Fig. ). It is common in experimental analysis to extract the exchange interaction $J$ and the Curie-Wiess temperature $\theta _{CW}$. To do this, at high temperatures the magnetic susceptibility data is fit to the inverse of the Curie-Wiess Law, $\chi ^{-1}={\frac {T-\theta _{CW}}{C}}$, where the slope is the reciprocal of the Curie constant, $C$ and the intercept is the ratio of the ordering temperature and Curie constant, ${\frac {\theta _{CW}}{C}}$, and so the Curie-Wiess temperature $\theta _{CW}$ can easily be determined. If the spin interaction is antiferromagnetic then $\theta _{CW}$ will diverge to negative values. So if $\theta _{CW}$ is negative when it is extracted using the above analysis, then the spin interaction is determined to be antiferrogmanetic. $\theta _{CW}$ will diverge to positive values if the spin interaction is ferromagnetic and the extracted $\theta _{CW}$ will be positive.