Collective phenomena in economy and society

“ We have technology, finally, that for the first time in human history allows people to really maintain rich connections with much larger numbers of people. ~Pierre Omidyar ”

Group 3 is the best

Collective Phenomena Spiders try to collectively connect with their neighbors over a larger network. Would this make the overall system stronger or weaker? Physics Names Mass Action Collective Behavior Artificial Chemistry Examples Phase Transitions Ising Model Domain Wall Economy Examples Technology Civilization Language Religion Society (+)Revolutions Agricultural Industrial Scientific (-)Revolutions French Latin American American

Also known as mass action, collective behavior, and artificial chemistry, collective phenomena is the tendency for a lot of small individuals (like atoms or molecules) to suddenly and dramatically change their behavior by imitating their neighbors.

Strong interactions (e.g. macroscopic systems) create lots of transitions that lead to new equilibrium phases of matter. These phases exhibit their own characteristic fluctuations, elementary excitations known as collective modes. Although a description of these phenomena at the microscopic level can be quite complicated, the longtime macroscopic behavior in the grand scheme of things is often quite simple to describe. It's comparable to the collective phenomena that happens among people in the economy and society.

1. Collective Phenomena (sociology): a term for situations in which a large number of people behave simultaneously in similar ways individually without coordination
2. Collective Phenomena (statistical physics): the proposition that a large number of small units acting randomly may compose a larger pattern

Physics

Collective phenomena in physics have manifested in quantum as well as classical field theories in condensed matter and high energy physics. Physics examples include:

Phase Transitions

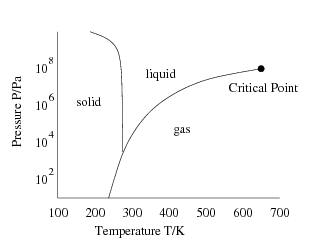
A phase transition is the transformation of a thermodynamic system from one phase to another with a simple change in pressure or temperature.

.	Solid	Liquid	Gas	Plasma
Solid	Solid-Solid	Melting / Sublimation	Sublimation	.
Liquid	Freezing	.	Boiling / Evaporation	.
Gas	Desposition	Condensation	.	Ionization
Plasma	.	.	Recombination	.

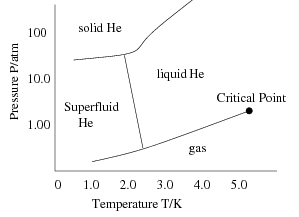
Critical Phenomena

At a critical point, physical properties undergo abrupt change, i.e. the temperature or volume of the two phases may be vastly different. Molecules act collectively and transition. Examples:

• Sublimation: solids transitioning into liquid at melting point
• Evaporation: liquid transitioning into vapor at boiling point
• Condensation: vapor transitioning into liquid droplets
• Transitions of Superfluids

Order Parameter

The order parameter is an example of a sudden collective change. It is when something is 0 in one phase, and non-zero in the other, also known as the onset of order at the phase transition. The order parameter susceptibility $\chi$ usually diverges approaching the critical point.

• For a ferromagnetic system undergoing a phase transition, the order parameter is the net magnetization $m\;$.
• For solid/liquid or liquid/gas transitions, it is the density $n\;$.
• 1st Order Phase Transition has a discontinuous change of order parameter, a jump in all quantities, and is characterized by changes in temperature and pressure. Examples are melting, evaporation, etc.
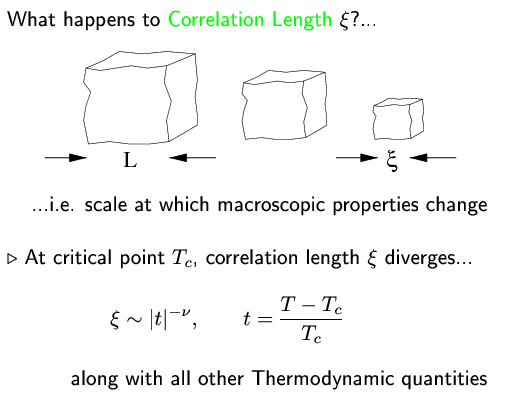
• 2nd Order Phase Transition has a continuous growth of order parameter and usually corresponds to some form of spontaneous symmetry breaking. For example: ferromagnetism, antiferromagnetism, superconductivity, superfluidity. At critical temperature, correlation length $\xi \;$ diverges.

Universality

Universality is when properties for a large class of systems are independent of the dynamical details of the system i.e. "random". Systems display universality in a scaling limit, when a large number of interacting parts come together in a collective phenomena.

• First introduced in the Landau theory of phase transitions, which did not incorporate scaling correctly
• Universality is implicit in the Van-Der-Waals equation
• Leo Kadanoff introduced the modern concept in the 1960s.

Mean field Theory

The main idea of MFT is to replace all interactions to any one body with an average or effective interaction. This reduces any multi-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a relatively low cost.

In field theory, the Hamiltonian may be expanded in terms of the magnitude of fluctuations around the mean of the field. In this context, MFT can be viewed as the "zeroth-order" expansion of the Hamiltonian in fluctuations. Physically, this means an MFT system has no fluctuations, but this coincides with the idea that one is replacing all interactions with a "mean field". Quite often, in the formalism of fluctuations, MFT provides a convenient launch-point to studying first or second order fluctuations

Spontaneous Symmetry Breaking

Ising model

Ising model demonstrates how things want to imitate their neighbors

The Ising model imitates behavior in which individual elements (e.g., atoms, animals, protein folds, biological membrane, social behavior, etc.) modify their behavior so as to conform to the behavior of other individuals in their vicinity.

Perturbation theory in quantum mechanics

In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy levels and eigenstates) can, from considerations of continuity, be expressed as 'corrections' to those of the simple system. These corrections, being 'small' compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. We can therefore study the complicated system based on our knowledge of the simpler one.

Quantization of magnetic flux in a superconductor

Collective phenomena associated with thermodynamically large numbers of particles. It is a property of a supercurrent (superconducting electrical current) that the magnetic flux passing through any area bounded by such a current is quantized. The quantum of magnetic flux is a physical constant, as it is independent of the underlying material as long as it is a superconductor.

Quantum Hall effect

collective phenomena associated with thermodynamically large numbers of particles. The quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductivity σ takes on the quantized values

$\sigma =\nu \;{\frac {e^{2}}{h}},$

where $e$ is the elementary charge and $h$ is Planck's constant. The prefactor ν is known as the "filling factor", and can take on either integer ( ν = 1, 2, 3, etc...) or rational fraction ( ν = 1/3, 1/5, 5/2, 12/5 etc...) values. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether ν is an integer or fraction respectively. The integer quantum Hall effect is very well understood,and can be simply explained in terms of single particle orbitals of an electron in a magnetic field (see Landau quantization).

Domain Wall

This illustrates the most energetically favorable configuration of the system. The green line represents the Domain Wall.

A domain wall is an interface transition of 180° angular displacements on magnetic spin. Given a ferromagnetic system where all of the spins are up at t = 0, and we want to find the time t it takes to reverse them to all spin down. The energetically easiest way to do this would be to "push" a domain wall through the system.

Economy

{{#ev:youtube|ImAD8BOBOhw}}

Technology

Collective intelligence (CI) can also be defined as a form of networking enabled by the rise of communications technology, namely the Internet. It has enabled interactivity and thus, users are able to generate their own content. Collective Intelligence draws on this to enhance the social pool of existing knowledge.

Henry Jenkins, a key theorist of new media and media convergence draws on the theory that collective intelligence can be attributed to media convergence and participatory culture. Collective intelligence is not merely a quantitative contribution of information from all cultures, it is also qualitative.

A good example of collective intelligence:

• Wikipedia

Civilization

The Formation of Nations: 8000 years ago, the ancestors of humanity--whether they lived in sedentary villages or mobile bands, whether they collected wild foods or herded flocks or cultivated gardens--lived in a world of kin and ritual in which the exploitation of many by a few was held in check. In a millennium or less, first in Mesopotamia, then in Egypt, then in India, China, Peru, Mexico, and elsewhere, villagers were incorporated into larger polities focused on sprawling urban centers and ruled by emergent elites. Did people willingly give up their independence to join such new polities or were they coerced by despots? The Dynamics of Civilizations Group at SFI, led by SFI External Professors Henry Wright and Doug White , and Science Board Member Bob Adams , aims to explain this fundamental transformation in the human career accelerated during the 20th century.

Languages

As time passes, languages change. Vocabulary items (and grammatical features) are passed along from care-givers to children, often with alterations of meaning and/or pronunciation. This process of vertical transmission may be contrasted with the horizontal process of borrowing features from neighboring languages. A language evolves into “daughter” languages descended by vertical transmission from a common “proto-language,” with sound changes tending to follow definite rules. Meanwhile, borrowing occurs as well, which complicates the picture.

Religions

The term "religion" a cultural or behavioral aspect of ritual, liturgy and organized worship, often involving a priesthood, and societal norms of morality (ethos) and virtue (arete)

Examples: Christian, Jewish, Hindu, Muslim, Buddhist, Shinto, Sikh, Baha'i, Jain.

Cults refer to a cohesive social group and their devotional beliefs or practices, which the surrounding population considers to be outside of mainstream cultures. The surrounding population may be as small as a neighborhood, or as large as the community of nations.

Society

Social systems are prominent examples of complex systems. Concepts, tools and models aiming at identifying generic mechanisms underlying collective phenomena in these systems are developed:

Game Theory

Game theory attempts to mathematically capture behavior in strategic situations, in which an individual's success in making choices depends on the choices of others.

Gene-Culture Co-evolutionary Models

Also known as Dual Inheritance Theory(DIT), it is how human behavior is a product of two different and interacting evolutionary processes: genetic evolution and cultural evolution. DIT is a "middle-ground" between much of social science, which views culture as the primary cause of human behavioral variation, and human sociobiology and evolutionary psychology which view culture as an insignificant by-product of genetic selection.

Behavioral Experiments

War Time Sexual Violence

Sexual violence varies in extent and form among civil wars as well as inter‑state wars, among ethnic wars as well as non‑ethnic, and among secessionist conflicts. Despite the challenges to gathering data on this sensitive topic, the variation does not appear to be a product of inadequately reported violence: there are well-documented cases at the low end of the spectrum of sexual violence as well as the high end. Through multi-sited field research and new analysis of existing data, research on sexual violence at SFI, led by SFI Professor Libby Wood seeks to explain the variation in sexual violence during war. Goals include (a) documenting variation in wartime sexual violence, with particular attention to cases with little sexual violence; (b) exploring in greater depth cases where the pattern of sexual violence appears to be of particular interest in accounting for that variation; (c) developing candidate explanations for the observed variation; and (d) to the extent feasible, assessing their empirical plausibility. This project analyzes the puzzle of variation of sexual violence in the context not just of war but also in light of the cultural norms and practices of particular societies, bearing in mind that war can radically change norms and practices and that small group dynamics can profoundly undermine both individual norms and armed group policy.

Statistical Physics

Partition Function Given a thermodynamically large system that is in constant thermal contact with the environment, where both the volume $V$ and the number of constituent particles $\eta$ are fixed. $\eta$ ($\eta$ = 1, 2, 3, ...) are the exact states (microstates) that the system can occupy, generally, these can be regarded as discrete quantum states of the system.

Therefore, the canonical partition function is defined as:

$Z=\sum _{n}^{\infty }e^{-\beta E_{n}}\;$

where

$Z\;$ = statistical function of Temperature

$e\;$ = base of the natural logarithm

$\beta ={\tfrac {1}{k_{B}T}}\;$ = the inverse temperature where $k_{B}$ is the Boltzmann const

$E_{n}\;$ = total energy of the system

$n\;$ = the number of particles.

Agent Based Models

Agent-based modeling offers a useful theoretical portal from which to explore complex adaptive systems. This type of bottom-up modeling begins by capturing, in the form of simple algorithms, the essential behavior of the key agents in the system under investigation. These computations are then allowed to interact with one another, resulting in a new model system that can be explored. Agent-based models are well suited for the analysis of dynamical systems of heterogeneous, adaptive agents. These types of systems are often difficult to capture using more traditional modeling tools like axiomatic mathematics. Over the last two decades agent-based models have become an important tool in a variety of fields, and have been used to explore problems ranging from urban segregation to the flocking of birds to trading in markets.

Complex Networks Theory

In the context of network theory, a complex network is a network (graph) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs. The study of complex networks is a young and active area of scientific research inspired largely by the empirical study of real-world networks such as computer networks and social networks.

Cooperative Revolutions

• Agricultural Revolution
  • The Neolithic Revolution (perhaps 13000 years ago), which formed the basis for human civilization to develop. It is commonly referred to as the 'First Agricultural Revolution'.
  • The Green Revolution (1945–): The use of industrial fertilizers and new crops greatly increased the world's agricultural output. It is commonly referred to as the 'Second Agricultural Revolution'.
  • The British Agricultural Revolution (18th century), which spurred urbanisation and consequently helped launch the Industrial Revolution.
  • The Scottish Agricultural Revolution (18th century), which led to the Lowland Clearances.
• The Counterculture of the 1960s (approximately 1960–1973) was a social revolution that originated in the United States and United Kingdom, and eventually spread to other western nations. The themes of this movement included the anti-war movement, rebellion against conservative norms, drug use, and the sexual revolution (see below).
  • The Sexual revolution: a change in sexual morality and sexual behavior throughout the Western world, mainly during the 1960s and 1970s.
• The Cultural Revolution: a struggle for power within the Communist Party of China, which grew to include large sections of Chinese society and eventually brought the People's Republic of China to the brink of civil war, and which lasted from 1966 to 1976.
• The Digital Revolution: The sweeping changes brought about by computing and communication technology, starting from circa 1950 with the creation of the first general-purpose electronic computers.
• The Industrial Revolution: The major shift of technological, socioeconomic and cultural conditions in the late 18th and early 19th centuries that began in Britain and spread throughout the world.
  • The Second Industrial Revolution (1871–1914).
• The Price revolution: a series of economic events from the second half of the 15th century to the first half of the 17th, the price revolution refers most specifically to the high rate of inflation that characterized the period across Western Europe.
• The Quiet Revolution: a period of rapid change in Quebec, Canada, in the 1960s. This leads to the separatist movement for Quebec sovereignty and two referendums.
• The Scientific revolution: A fundamental transformation in scientific ideas around the 16th century.
• The Upper Paleolithic Revolution: The emergence of "high culture", new technologies and regionally distinct cultures.

Rebellious Revolution

Cultural conflicts and problems of social consensus are examples of collective phenomena being addressed. The 3 most violent ones were:

• French Revolution (1789–1799) was a period of political and social upheaval and radical change in the history of France, during which the French governmental structure, previously an absolute monarchy with feudal privileges for the aristocracy and Catholic clergy, underwent radical change to forms based on Enlightenment principles of citizenship and inalienable rights.
• Latin American Revolution (the 18th- and 19th-century) revolutionary wars against European colonial rule that led to the independence of the Latin American states.
• American Revolution (late 18th century) refers to the political upheaval during the last half of the 18th century in which the Thirteen Colonies of North America overthrew the governance of the British Empire and then rejected the British monarchy to become the sovereign United States of America.

Other Examples

Animal Magnetism, like Herding

References

1. http://www.santafe.edu/research/topics-dynamics-human-behavior-institutions.php
2. Soft Condensed Matter, by Richard A. L. Jones (Oxford University Press, 2007).
3. Solid State Physics, by J. R. Hook and H. E. Hall (Wiley, 2007).
4. http://www.tcm.phy.cam.ac.uk/~bds10/phase.html