Collective phenomena in economy and society: Difference between revisions
(Infobox) |
|||
| Line 22: | Line 22: | ||
|- valign="top" | |- valign="top" | ||
| '''Examples''' | | '''Examples''' | ||
| | | Technology <br>Civilization <br>Language <br>Religion | ||
|- | |- | ||
! colspan="2" style="background:#ccffff;"| Society | ! colspan="2" style="background:#ccffff;"| Society | ||
|- valign="top" | |- valign="top" | ||
| ''' | | '''(+) Revolutions''' | ||
| | | Agricultural<br> Industrial <br>Scientific | ||
|- valign="top" | |||
| '''(-) Revolutions''' | |||
| French Revolution <br>Latin American Revolution <br> American Revolution | |||
|} | |} | ||
<!-- END OF EMBEDDED TABLE --> | <!-- END OF EMBEDDED TABLE --> | ||
Revision as of 11:44, 22 April 2009
“ We have technology, finally, that for the first time in human history allows people to really maintain rich connections with much larger numbers of people. ~Pierre Omidyar ”
| ||||||||||||||||
Also known as mass action, collective behavior, and artificial chemistry, collective phenomena is the tendency for a lot of small individuals (like atoms or molecules) to suddenly and dramatically change their behavior by imitating their neighbors.
Strong interactions (e.g. macroscopic systems) create lots of transitions that lead to new equilibrium phases of matter. These phases exhibit their own characteristic fluctuations, elementary excitations known as collective modes. Although a description of these phenomena at the microscopic level can be quite complicated, the longtime macroscopic behavior in the grand scheme of things is often quite simple to describe. It's comparable to the collective phenomena that happens among people in the economy and society.
- Collective Phenomena (sociology): a term for situations in which a large number of people behave simultaneously in similar ways individually without coordination
- Collective Phenomena (statistical physics): the proposition that a large number of small units acting randomly may compose a larger pattern
Physics
Phenomenal approaches based on this concept have led to certain quantum as well as classical field theories that over recent years have played a major role in shaping our understanding of condensed matter and high energy physics.
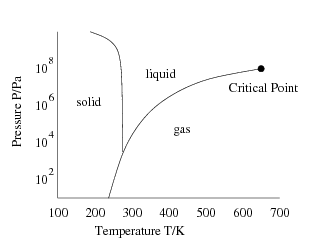
Phase Transitions
A phase transition is the transformation of a thermodynamic system from one phase to another.
| . | Solid | Liquid | Gas | Plasma |
| Solid | Solid-Solid | Melting / Sublimation | Sublimation | . |
| Liquid | Freezing | Boiling / Evaporation | . | . |
| Gas | Desposition | Condensation | . | Ionization |
| Plasma | . | . | Recombination | . |
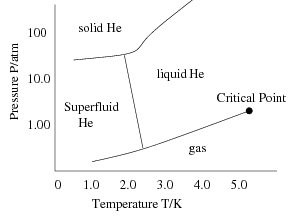
Critical Phenomena
At a critical point, physical properties undergo abrupt change, i.e. the temperature or volume of the two phases may be vastly different. Examples:
- evaporation: liquid water transitioning into vapor at boiling point
- condensation: of vapor transitioning into liquid droplets
Order Parameter
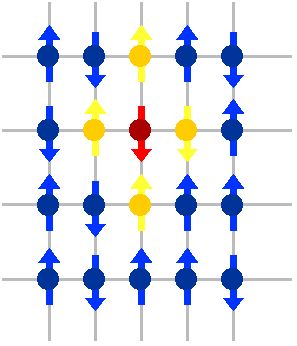
The order parameter is normally a quantity which is 0 in one phase, usually above the critical point and non-zero in the other. It characterises the onset of order at the phase transition. The order parameter susceptibility will usually diverge approaching the critical point. For a ferromagnetic system undergoing a phase transition, the order parameter is the net magnetization. For solid/liquid or liquid/gas transitions, it is the density.
- 1st Order Phase Transition has a discontinuous change of order parameter. A first order phase transition displays a jump in all quantities, and is characterized by a latent heat. Examples are melting, evaporation, etc.
- 2nd Order Phase Transition has a continuous growth of order parameter. A second order phase transition is continuous and usually corresponds to some form of spontaneous symmetry breaking. For example: ferromagnetism, antiferromagnetism, superconductivity, superfluidity. At critical temperature, correlation length diverges.
Superfluids
Universality
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together. The modern meaning of the term was introduced by Leo Kadanoff in the 1960s, but a simpler version of the concept was already implicit in the Van-Der-Waals equation and in the earlier Landau theory of phase transitions, which did not incorporate scaling correctly.
Mean field Theory
The main idea of MFT is to replace all interactions to any one body with an average or effective interaction. This reduces any multi-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a relatively low cost.
In field theory, the Hamiltonian may be expanded in terms of the magnitude of fluctuations around the mean of the field. In this context, MFT can be viewed as the "zeroth-order" expansion of the Hamiltonian in fluctuations. Physically, this means an MFT system has no fluctuations, but this coincides with the idea that one is replacing all interactions with a "mean field". Quite often, in the formalism of fluctuations, MFT provides a convenient launch-point to studying first or second order fluctuations
Spontaneous Symmetry Breaking
Ising model
The Ising model imitates behavior in which individual elements (e.g., atoms, animals, protein folds, biological membrane, social behavior, etc.) modify their behavior so as to conform to the behavior of other individuals in their vicinity.
Perturbation theory in quantum mechanics
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy levels and eigenstates) can, from considerations of continuity, be expressed as 'corrections' to those of the simple system. These corrections, being 'small' compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. We can therefore study the complicated system based on our knowledge of the simpler one.
Quantization of magnetic flux in a superconductor
collective phenomena associated with thermodynamically large numbers of particles. It is a property of a supercurrent (superconducting electrical current) that the magnetic flux passing through any area bounded by such a current is quantized. The quantum of magnetic flux is a physical constant, as it is independent of the underlying material as long as it is a superconductor. Its value is = 2.067 833 636Template:E
Quantum Hall effect
collective phenomena associated with thermodynamically large numbers of particles. The quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductivity σ takes on the quantized values
where is the elementary charge and is Planck's constant. The prefactor ν is known as the "filling factor", and can take on either integer ( ν = 1, 2, 3, etc...) or rational fraction ( ν = 1/3, 1/5, 5/2, 12/5 etc...) values. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether ν is an integer or fraction respectively. The integer quantum Hall effect is very well understood,and can be simply explained in terms of single particle orbitals of an electron in a magnetic field (see Landau quantization).
Economy
{{#ev:youtube|ImAD8BOBOhw}}
Technology
Collective intelligence (CI) can also be defined as a form of networking enabled by the rise of communications technology, namely the Internet. Web 2.0 has enabled interactivity and thus, users are able to generate their own content. Collective Intelligence draws on this to enhance the social pool of existing knowledge. Henry Jenkins, a key theorist of new media and media convergence draws on the theory that collective intelligence can be attributed to media convergence and participatory culture.[1] Collective intelligence is not merely a quantitative contribution of information from all cultures, it is also qualitative.
One CI pioneer, George Pór, defined the collective intelligence phenomenon as "the capacity of human communities to evolve towards higher order complexity and harmony, through such innovation mechanisms as differentiation and integration, competition and collaboration."[2] Tom Atlee and George Pór state that "collective intelligence also involves achieving a single focus of attention and standard of metrics which provide an appropriate threshold of action". Their approach is rooted in Scientific Community Metaphor.
Levy and de Kerckhove consider CI from a mass communications perspective, focusing on the ability of networked ICT’s to enhance the community knowledge pool. They suggest that these communications tools enable humans to interact and to share and collaborate with both ease and speed (Flew 2008). With the development of the Internet and its widespread use, the opportunity to contribute to community-based knowledge forums, such as Wikipedia, is greater than ever before. These computer networks give participating users the opportunity to store and to retrieve knowledge through the collective access to these databases and allow them to “harness the hive” (Raymond 1998; Herz 2005 in Flew 2008).
Researchers[3] at the MIT Center for Collective Intelligence research and explore collective intelligence of groups of people and computers.
Civilization
The Formation of Nations: 8000 years ago, the ancestors of humanity--whether they lived in sedentary villages or mobile bands, whether they collected wild foods or herded flocks or cultivated gardens--lived in a world of kin and ritual in which the exploitation of many by a few was held in check. In a millennium or less, first in Mesopotamia, then in Egypt, then in India, China, Peru, Mexico, and elsewhere, villagers were incorporated into larger polities focused on sprawling urban centers and ruled by emergent elites. Did people willingly give up their independence to join such new polities or were they coerced by despots? The Dynamics of Civilizations Group at SFI, led by SFI External Professors Henry Wright and Doug White , and Science Board Member Bob Adams , aims to explain this fundamental transformation in the human career accelerated during the 20th century.
Languages
As time passes, languages change. Vocabulary items (and grammatical features) are passed along from care-givers to children, often with alterations of meaning and/or pronunciation. This process of vertical transmission may be contrasted with the horizontal process of borrowing features from neighboring languages. A language evolves into “daughter” languages descended by vertical transmission from a common “proto-language,” with sound changes tending to follow definite rules. Meanwhile, borrowing occurs as well, which complicates the picture.
Religions
The term "religion" a cultural or behavioural aspect of ritual, liturgy and organized worship, often involving a priesthood, and societal norms of morality (ethos) and virtue (arete)
Society
Society shows sometimes abrupt changes - revolutions - which are related to phase transitions: both are sudden and dramatic changes of behavior.
Social systems are prominent examples of complex systems. Concepts, tools and models aiming at identifying generic mechanisms underlying collective phenomena in these systems are developed with the use of
Game Theory
Game theory attempts to mathematically capture behavior in strategic situations, in which an individual's success in making choices depends on the choices of others.
Gene-Culture Co-evolutionary Models
Also known as Dual Inheritance Theory(DIT), it is how human behavior is a product of two different and interacting evolutionary processes: genetic evolution and cultural evolution. DIT is a "middle-ground" between much of social science, which views culture as the primary cause of human behavioral variation, and human sociobiology and evolutionary psychology which view culture as an insignificant by-product of genetic selection.
Behavioral Experiments
War Time Sexual Violence
Sexual violence varies in extent and form among civil wars as well as inter‑state wars, among ethnic wars as well as non‑ethnic, and among secessionist conflicts. Despite the challenges to gathering data on this sensitive topic, the variation does not appear to be a product of inadequately reported violence: there are well-documented cases at the low end of the spectrum of sexual violence as well as the high end. Through multi-sited field research and new analysis of existing data, research on sexual violence at SFI, led by SFI Professor Libby Wood seeks to explain the variation in sexual violence during war. Goals include (a) documenting variation in wartime sexual violence, with particular attention to cases with little sexual violence; (b) exploring in greater depth cases where the pattern of sexual violence appears to be of particular interest in accounting for that variation; (c) developing candidate explanations for the observed variation; and (d) to the extent feasible, assessing their empirical plausibility. This project analyzes the puzzle of variation of sexual violence in the context not just of war but also in light of the cultural norms and practices of particular societies, bearing in mind that war can radically change norms and practices and that small group dynamics can profoundly undermine both individual norms and armed group policy.
Statistical Physics
Partition Function Given a thermodynamically large system that is in constant thermal contact with the environment, where both the volume and the number of constituent particles are fixed. ( = 1, 2, 3, ...) are the exact states (microstates) that the system can occupy, generally, these can be regarded as discrete quantum states of the system.
Therefore, the canonical partition function is defined as:
where
- = statistical function of Temperature
- = base of the natural logarithm
- = the inverse temperature where is the Boltzmann const
- = total energy of the system
- = the number of particles.
Agent Based Models
Agent-based modeling offers a useful theoretical portal from which to explore complex adaptive systems. This type of bottom-up modeling begins by capturing, in the form of simple algorithms, the essential behavior of the key agents in the system under investigation. These computations are then allowed to interact with one another, resulting in a new model system that can be explored. Agent-based models are well suited for the analysis of dynamical systems of heterogeneous, adaptive agents. These types of systems are often difficult to capture using more traditional modeling tools like axiomatic mathematics. Over the last two decades agent-based models have become an important tool in a variety of fields, and have been used to explore problems ranging from urban segregation to the flocking of birds to trading in markets. SFI External Professors George Gumerman and Tim Kohler and others are simulating ancient societies of the southwest, SFI Professor Steve Lansing is modeling the relation between rule based marriage and genetic relatedness in Bali, and SFI External Professors John Miller and Scott Page are modeling complex adaptive social systems using thoughtful agents.
Complex Networks Theory
In the context of network theory, a complex network is a network (graph) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs. The study of complex networks is a young and active area of scientific research inspired largely by the empirical study of real-world networks such as computer networks and social networks.
Cooperation
- Agricultural Revolution
- The Neolithic Revolution (perhaps 13000 years ago), which formed the basis for human civilization to develop. It is commonly referred to as the 'First Agricultural Revolution'.
- The Green Revolution (1945–): The use of industrial fertilizers and new crops greatly increased the world's agricultural output. It is commonly referred to as the 'Second Agricultural Revolution'.
- The British Agricultural Revolution (18th century), which spurred urbanisation and consequently helped launch the Industrial Revolution.
- The Scottish Agricultural Revolution (18th century), which led to the Lowland Clearances.
- The Counterculture of the 1960s (approximately 1960–1973) was a social revolution that originated in the United States and United Kingdom, and eventually spread to other western nations. The themes of this movement included the anti-war movement, rebellion against conservative norms, drug use, and the sexual revolution (see below).
- The Sexual revolution: a change in sexual morality and sexual behavior throughout the Western world, mainly during the 1960s and 1970s.
- The Cultural Revolution: a struggle for power within the Communist Party of China, which grew to include large sections of Chinese society and eventually brought the People's Republic of China to the brink of civil war, and which lasted from 1966 to 1976.
- The Digital Revolution: The sweeping changes brought about by computing and communication technology, starting from circa 1950 with the creation of the first general-purpose electronic computers.
- The Industrial Revolution: The major shift of technological, socioeconomic and cultural conditions in the late 18th and early 19th centuries that began in Britain and spread throughout the world.
- The Second Industrial Revolution (1871–1914).
- The Price revolution: a series of economic events from the second half of the 15th century to the first half of the 17th, the price revolution refers most specifically to the high rate of inflation that characterized the period across Western Europe.
- The Quiet Revolution: a period of rapid change in Quebec, Canada, in the 1960s. This leads to the separatist movement for Quebec sovereignty and two referendums.
- The Scientific revolution: A fundamental transformation in scientific ideas around the 16th century.
- The Upper Paleolithic Revolution: The emergence of "high culture", new technologies and regionally distinct cultures.
Revolution
Cultural conflicts and problems of social consensus are examples of phenomena being addressed.
- French Revolution
- Latin American Revolution
- American Revolution
Other Examples
Animal Magnetism, like Herding
References
- ↑ Flew, T. (2008). New Media: an introduction. Melbourne: Oxford University Press
- ↑ George Pór, Blog of Collective Intelligence
- ↑ http://cci.mit.edu/people/index.html
- http://www.santafe.edu/research/topics-dynamics-human-behavior-institutions.php
- Soft Condensed Matter, by Richard A. L. Jones (Oxford University Press, 2007).
- Solid State Physics, by J. R. Hook and H. E. Hall (Wiley, 2007).
- http://www.tcm.phy.cam.ac.uk/~bds10/phase.html