Phy5670: Difference between revisions
Oskarvafek (talk | contribs) |
Oskarvafek (talk | contribs) |
||
| Line 35: | Line 35: | ||
or, in artificial cases, perhaps for a highly restricted subset of all configurations. | or, in artificial cases, perhaps for a highly restricted subset of all configurations. | ||
</tt> P.W. Anderson (''Basic Notions of Condensed Matter Physics'')</blockquote> | </tt> P.W. Anderson (''Basic Notions of Condensed Matter Physics'')</blockquote> | ||
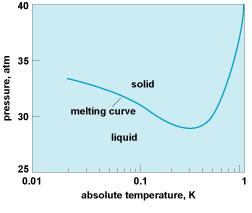
[[Image:He3meltingCurve.JPG ]] | [[Image:He3meltingCurve.JPG|thumb|600px|right|The melting curve of He3 at low temperature from E. R.Grilly, J. Low Temp. Phys., 11:33–52, 1973. Note that for a range of pressures, the solid He3 melts upon cooling(!). The reason behind such anomaly has its origin in solid having a greater paramagnetic entropy than (Fermi) liquid.]] | ||
==== Role played by the Thermodynamic limit <math>N\rightarrow \infty</math> ==== | ==== Role played by the Thermodynamic limit <math>N\rightarrow \infty</math> ==== | ||
Revision as of 21:28, 23 August 2010
Welcome to the Quantum Many Body Physics PHY5670 Fall2010
PHY5670 is a one semester graduate level course. Its aim is to introduce basic concepts, and logical framework, of this vast and developing discipline: broken symmetry and adiabatic continuity. Theoretical techniques, such as coherent state path integrals and diagrammatic perturbation expansions, will be used to emphasize these deeper underlying concepts, as well as to provide practical means of calculations. Few illustrative physical systems and quantum many-body models will also be studied.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments: Fall 2010 student teams
Outline of the course:
Conceptual basis of many body physics
Broken symmetry
Our experience shows us, then, that as matter cools down it usually no longer retains the full symmetry of the basic laws of quantum mechanics which it undoubtedly obeys; our task here is to understand that the questions we must ask are "Why", "In what sense", and "What are the consequences?" P.W. Anderson (Basic Notions of Condensed Matter Physics)
"Why?" broken symmetry
Under surprisingly general circumstances the lowest energy state of a system does not have the total symmetry group of its Hamiltonian, and so in the absence of thermal fluctuations the system assumes an unsymmetrical state. P.W. Anderson (Basic Notions of Condensed Matter Physics)
Examples: Wigner crystallization and He-3
At low density, electrons in the jellium model crystalize into a bcc Wigner crystal. At high density (and sufficiently finite temperature) they behave as Fermi gas/liquid with all the invariance properties of the ordinary Boltzman gas, which this system is when .
If we compress a high enough density Fermi liquid with short range repulsive interactions, approximately as , it will form a regular solid.
The essential phenomenon is either case is that the lowest state of a potential energy of interaction between the particles -- for example, a pair interaction
-- must occur for either a unique relative configuration of all particles and all translations and rotations, or, in artificial cases, perhaps for a highly restricted subset of all configurations.
P.W. Anderson (Basic Notions of Condensed Matter Physics)
Role played by the Thermodynamic limit
"What are the consequences?" of broken symmetry
- discreteness of phase transitions, and the resulting failure of continuation: disjointness of physical phases
- development of collective excitations
- generalized rigidity
- defect structures: dissipation and topological considerations