Phy5670: Difference between revisions
| Line 81: | Line 81: | ||
The transition between states of different symmetry can be characterized in terms of an | ===== Symmetry breaking and the thermodynamic limit ===== | ||
The transition between states of different symmetry can be characterized in terms of an ''order parameter, which is defined (in the sense of Landau) as any parameter, that is zero in the symmetric phase and non-zero in the broken symmetry phase''. | |||
In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter since it is forced to zero by virtue of the symmetry. | In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter since it is forced to zero by virtue of the symmetry. | ||
| Line 88: | Line 91: | ||
Another way to see the necessity of the thermodynamic limit is to use by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system is initially in an <math>\upuparrows </math> state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to <math>\uparrow \downarrow </math> or <math>\downarrow \uparrow</math>. In order to minimize energy, the spins will realign. However, the return to the initial <math>\upuparrows </math> state is just as likely as the transition to the <math>\downdownarrows </math>. Over time, the system will be found in the <math>\upuparrows </math> state just as often as in the <math>\downdownarrows </math> state, and the overall magnetization will be zero. | Another way to see the necessity of the thermodynamic limit is to use by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system is initially in an <math>\upuparrows </math> state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to <math>\uparrow \downarrow </math> or <math>\downarrow \uparrow</math>. In order to minimize energy, the spins will realign. However, the return to the initial <math>\upuparrows </math> state is just as likely as the transition to the <math>\downdownarrows </math>. Over time, the system will be found in the <math>\upuparrows </math> state just as often as in the <math>\downdownarrows </math> state, and the overall magnetization will be zero. | ||
This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped simultaneously in order for the system to go from <math>\uparrow \uparrow \uparrow \ldots </math> to <math>\downarrow \downarrow \downarrow \ldots </math>, and the typical time span the system needs to change from one ground state into another grows. For a system with <math>N=\infty </math>, ergodicity is broken | This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped simultaneously in order for the system to go from <math>\uparrow \uparrow \uparrow \ldots </math> to <math>\downarrow \downarrow \downarrow \ldots </math>, and the typical time span the system needs to change from one ground state into another grows. For a system with <math>N=\infty </math>, ergodicity is broken, because even if each ground state is in principle equally likely, the system will stay in its initial state forever. | ||
Of couse, no real ferromagnet, crystal or other experimental system is truly infinite. However, typical macroscopic system sizes of <math>N=10^{23}</math> are enough to make the lifetime of any intial ground state longer than the age of the universe. The system is frozen into one particular ground state; the symmetry connecting different ground states is dynamically broken. | |||
By reversion of this argument, it is easy to see that no spontaneous symmetry breaking is possible in any microscopic system, such as molecules. | |||
Many phase transitions that exhibit symmetry breaking are ''second order'' or ''continous phase transitions''. Examples are ferromagnets, antiferromagnets or superconductors. Second order phase transitions do not - in contrast to first order phase transitions - involve latent heat. An example of a first order phase transition with symmetry breaking is the liquid-to-solid-transition. The transition from liquid to gas is also of first order, but involves no symmetry change. | |||
The distinction between phase transitions with and without symmetry breaking is very important, since the phenomena that can occur in each state are dictated by the symmetry exhibited. For example, it is only possible to get from one phase into another without crossing a phase border if both phases exhibit the same symmetry (as liquid and gaseous water), while phases with different symmetries are necessarily disjoint. These issues will be discussed in more detail in chapter 1.1.2. | |||
===== Examples ===== | ===== Examples ===== | ||
Revision as of 18:53, 8 October 2010
Welcome to the Quantum Many Body Physics PHY5670 Fall2010
PHY5670 is a one semester graduate level course. Its aim is to introduce basic concepts, and logical framework, of this vast and developing discipline: broken symmetry and adiabatic continuity. Theoretical techniques, such as coherent state path integrals and diagrammatic perturbation expansions, will be used to emphasize these deeper underlying concepts, as well as to provide practical means of calculations. Few illustrative physical systems and quantum many-body models will also be studied.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments: Fall 2010 student teams
Outline of the course:
Conceptual basis of many body physics
Broken symmetry
What is broken symmetry?
Our experience shows us, then, that as matter cools down it usually no longer retains the full symmetry of the basic laws of quantum mechanics which it undoubtedly obeys; our task here is to understand that the questions we must ask are "Why", "In what sense", and "What are the consequences?" P.W. Anderson (Basic Notions of Condensed Matter Physics)
In a system of many particles there could be many different kind of interactions between them that dictated the behavior of the system when it pass through different regions of the parameters space. For example we can think in one system where the potential interaction is predominant compare to the kinetic energy, but obviously this is not necessarily true for all the possible configuration of the system (at least not in general for all the systems). Therefore, in each different system there could be present many kind of symmetries and depending in which configuration is the system will be the different presented symmetries.
Talking about the different symmetries probably the easy one to use as example would be the translational symmetry. Imagine that you have a system of particles with homogeneous properties in the space, then it doesn't matter if you do a translation in the system you should still see exactly the same properties. A crystal is obviously not this kind of system because it has fix positions for the particles, therefore if you translate the system an arbitrary distance probably the density (which is not homogeneous, you only have a probability to find particles in a lattice position rather than everywhere) will not be longer exactly the same than the previous one. In this sense we can say that when we have a crystallization in the system the translational symmetry is broke.
In a similar way than the translational symmetry, the rotational symmetry tell us about the isotropy of the system. As example we can cite a crystal system, where each particle has a magnetic dipole pointing randomly. If we apply a magnetic field to the system pointing in some constant direction the different dipoles will tray to be align to this external field. Therefore we will have a broke rotational symmetry because right now there is a preferred direction.
Also we can talk about inversion and time-reversal symmetry which are a little bit more complicated to understand, but at the same time are responsible of many phenomenons.
In a natural way we could expect that many symmetries were compatible with the matter at considerable high temperatures, but when the temperatures gets down these symmetries are no longer valid as we have pointed in the previous examples. We need to clarify that not only the change in temperature is responsible for the broken symmetries and the presence of the different phases, as we will see in the different examples that we will discuss here.
Therefore we can talk about a change of phase when there is a broken symmetry. For example when a system turns from liquid to solid, or also when pass from paramagnet to a ferromagnet; are because have been presented a broken symmetry and obviously the system in different phases cannot be treat with the same ideas and we need to distinguish the considerations that we can apply to the different phases.
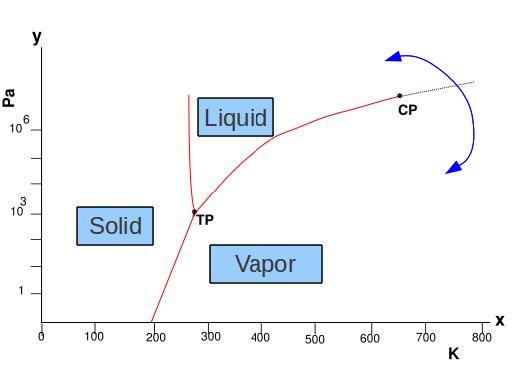
A point that should be clarify carefully is that when there is a change of phase could be because have been a broken symmetry, but this is not necessarily true. However, these are rare cases, but one should have present at least one example which is the change of phase from liquid water to vapor. In this case there is not a broken symmetry and one way to see it is because the critical point that exist in the water's phase diagram give us a chance to modify the system in such a way that liquid and vapor could coexist. We will talk a little more about this example.
"Why" broken symmetry?
Under surprisingly general circumstances the lowest energy state of a system does not have the total symmetry group of its Hamiltonian, and so in the absence of thermal fluctuations the system assumes an unsymmetrical state. P.W. Anderson (Basic Notions of Condensed Matter Physics)
The many-body theory has been applied to understand different phenomenons related to different type of systems and truthfully the most interesting are the most complicated to deal with. One goal that has been followed it's to understand the phases allow for a system related to its parameters, and how work the transitions between them.
One thing that have been observed for many physical systems with different kind of interactions between the particles of the system is that when it reach the lowest state of energy not all the symmetries are presented. As for example we could talk about the "Wigner solid" (see next section for details) which present a crystallization because the coulomb interactions dominate the kinetic energy.
The Wigner solid it's not the only example where a crystallization is presented at low temperatures. Actually, in general we can say that in any system where the potential energy interaction dominates the kinetic energy of the particles the crystallization will be present. This particular configuration for the system at low range of energies will be characteristic of each set of parameters involved.
The ideas that we have been checking about the broken symmetries under a change of phase could be present with any type of symmetry. As example we can talk about broken time-reversal invariance in systems as magnetic ordering, ferro and antiferromagnetic systems. In general these phenomena also break an at least approximate spin rotation symmetry. Liquid crystals exhibit another type: broken local rotational symmetry. Superconductivity is a broken gauge symmetry.
As conclusion we can say that in general the lowest-energy state of a system does not present the complete symmetry group of its Hamiltonian, and as consequence when the temperature of a system gets down we can expect that at some point an unsymmetrical state will appear.
The essential phenomenon is either case is that the lowest state of a potential energy of interaction between the particles -- for example, a pair interaction
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{tot}=\sum_{i<j}V(| r_i-r_j|)} -- must occur for either a unique relative configuration of all particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{r_1,r_2,\ldots r_N\}} and all translations and rotations,
or, in artificial cases, perhaps for a highly restricted subset of all configurations. P.W. Anderson (Basic Notions of Condensed Matter Physics)
It is then clear that in any situation where the potential energy dominates kinetic energy and entropy, as in the two cases mentioned, a system of particles obeying a simple potential will take up a regular lattice structure. P.W. Anderson (Basic Notions of Condensed Matter Physics)
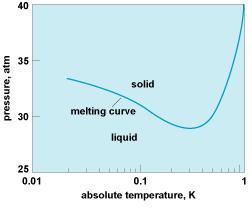
The less symmetric state tends to be one lower in temperature, simply because the more symmetric one is usually a distribution of thermal fluctuations among all the available values of the order parameter . But this order of phases is not a general rule; He3, for instance, violates it because the solid has a greater nuclear paramagnetic entropy than liquid, and at low temperatures the melting curve has a negative slope. So in this temperature regime, the solid is the high-temperature phase and the liquid is the low-temperature phase. P.W. Anderson (Basic Notions of Condensed Matter Physics)
Symmetry breaking and the thermodynamic limit
Symmetry breaking and the thermodynamic limit
The transition between states of different symmetry can be characterized in terms of an order parameter, which is defined (in the sense of Landau) as any parameter, that is zero in the symmetric phase and non-zero in the broken symmetry phase.
In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter since it is forced to zero by virtue of the symmetry.
The non-analycity of the free energy at the phase transition is only possible in the thermodynamic limit, i.e. for systems with infinite number of particles. The reason behind this is that any finite sum over the analytic functions describing the contribution to the free energy of each particle will again be analytic. However, an infinite sum of analytic functions can be non-analytic, very much like it a non-analytic step function can be expressed as the sum of an infinite Fourier sum over analytic trigonometric functions.
Another way to see the necessity of the thermodynamic limit is to use by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system is initially in an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \downarrow } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \uparrow} . In order to minimize energy, the spins will realign. However, the return to the initial Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state is just as likely as the transition to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } . Over time, the system will be found in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state just as often as in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } state, and the overall magnetization will be zero. This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped simultaneously in order for the system to go from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \uparrow \uparrow \ldots } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \downarrow \downarrow \ldots } , and the typical time span the system needs to change from one ground state into another grows. For a system with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\infty } , ergodicity is broken, because even if each ground state is in principle equally likely, the system will stay in its initial state forever.
Of couse, no real ferromagnet, crystal or other experimental system is truly infinite. However, typical macroscopic system sizes of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=10^{23}} are enough to make the lifetime of any intial ground state longer than the age of the universe. The system is frozen into one particular ground state; the symmetry connecting different ground states is dynamically broken.
By reversion of this argument, it is easy to see that no spontaneous symmetry breaking is possible in any microscopic system, such as molecules.
Many phase transitions that exhibit symmetry breaking are second order or continous phase transitions. Examples are ferromagnets, antiferromagnets or superconductors. Second order phase transitions do not - in contrast to first order phase transitions - involve latent heat. An example of a first order phase transition with symmetry breaking is the liquid-to-solid-transition. The transition from liquid to gas is also of first order, but involves no symmetry change.
The distinction between phase transitions with and without symmetry breaking is very important, since the phenomena that can occur in each state are dictated by the symmetry exhibited. For example, it is only possible to get from one phase into another without crossing a phase border if both phases exhibit the same symmetry (as liquid and gaseous water), while phases with different symmetries are necessarily disjoint. These issues will be discussed in more detail in chapter 1.1.2.
Examples
Wigner Crystals
At low density, electrons in the jellium model crystalize into a bcc Wigner crystal. At high density (and sufficiently finite temperature) they behave as Fermi gas/liquid with all the invariance properties of the ordinary Boltzman gas, which this system is when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>>E_F} .
He 3
If we compress a high enough density Fermi liquid with short range repulsive interactions, approximately as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He} , it will form a regular solid.
other examples
In the next chart we show and compare different systems that exhibit broken symmetry.
| Example | Disordered Phase | Ordered Phase | Order Parameter | Constant of motion? |
| Ferromagnetism | Paramagnet | Ferromagnet | Magnetization M | Yes |
| Antiferromagnetism | Paramagnet | Antiferromagnet | Sublattice magnetization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{sl}} | No |
| Superconductivity | Normal Metal | Superconductor | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\Psi_{\sigma}^*, \Psi_{-\sigma}^*> } | No |
| Crystal | Liquid | Solid | Density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_G} | No |
| He 3 | Normal liquid | Anisotropic superfluid | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ij}=<\Psi\Psi>_{M_L,M_S}} | No |
Note: To see more details and another phenomenons you can check "P.W. Anderson(Basic Notions of Condensed Matter Physics), pg.68"
As we can imagine there are just few examples were the order parameter is a constant of motion. The Ferromagnetism is one them.
"What are the consequences?" of broken symmetry
- Discreteness of phase transitions, and the resulting failure of continuation: disjointness of physical phases
- Development of collective excitations
- Generalized rigidity
- Defect structures: dissipation and topological considerations
Discreteness and Disjointness
First theorem "It is impossible to change symmetry gradually. A given symmetry element is either there or it is not; there is no way for it to grouw imperceptibly" (Landau and Lifshitz, 1958)
Let's analyze the phase diagram of the water (see figure above). As we can see in the diagram we can go from vapor to liquid in a "smooth path" just going around the critical point, actually this means that these two phases doesn't present a broken symmetry. On the other hand, it's impossible to go from liquid to solid smoothly (or in opposite way). The liquid-gas transition is typical of a symmetry-nonbreaking transition. There is no possibility that the fluid and gas can be in equilibrium at the same density except at a point on the boiling curve.
In the cases of true broken symmetry, the unsymmetrical state is normally characterized by and "order parameter". By Landau's definition this is simply any parameter that is zero in the symmetric state and has a nonzero average uniquely specifying state when the symmetry is broken; it is an additional variable necessary to specify the microscopic state in the lower symmetry state. Thus by broken symmetry a new variable is created. For example, in a nonmagnetic material the order parameter is the magnetization M, which in the absence of a magnetic field is zero by time-reversal symmetry and the state is specified by the usual intesive variables P and T.
It is possible to predict that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = -T \ln{<e^{-\beta H}>}} in the new system is a new mathematical function from than in the old. For instace, call the new variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Then in general we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = F(V,T,\psi)}
We calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = F(V,T)}
by appending to this the equilibium condition
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial F}{\partial \psi} = f = 0 }
where f is the generalized force variable (like the magnetic field H) corresponding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Above the critical temperature Tc, this is satisfied by symmetry; below, it is nontrivial. Then from the las two equations the result is a new function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F'(V,T) } , which is not analytic at Tc. This is Landau's essential insight.
In simplest terms, it is quite clear that the First Theorem requires that F have a boundary of singularities between the two regimes of symmetry, and that therefore analytic continuation between the two is not possible.
Collective excitations
At low enough temperatures the matter doesn't obey the initial symmetry, which the Hamiltonian of the system do. From this fact the most important and interesting properties of matter appear:
1. Affectation of the spectrum of elemetary excitations and fluctuations.
2. Causes a new static properties call "generalized rigidity".
In this sectio we will talk about the first consequence. The new state can be either an eienstate of H or not.
The original Hamiltonian has a group of symmetries G, and only when this group is a continuous one we can see dynamic effects at low temperature. G may be described by a set of generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i}
, i.e., the group elements A belonging to G
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AHA^{-1}=H}
may be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=e^{i\theta L_i}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i}
is related to infinitesimal transformations. For an infinitesimal transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=1+ i\epsilon L_i}
and continuous groups may in general be built up by products of infintesimal operators. The spin rotaion group, for instance, has the generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_x, S_y, S_z.}
The only unsymmetrical operators which commute with H are the various group generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i}
. These are therefore conserved quantities; and if the order parameter can be taken as one of them, it is conserved. For example in the case of ferromagnets the order parameter may be taken as the total spin in some fixed direction z. That may well be the only example of a simple, conserved order parameter.
The "dimensionality of the order parameter" plays a great role in critical fluctuation theory. When the violated symmetry is only that of a point group (a discrete symmetry) we speak of a "one dimensional order parameter". An example is the Ising model for ferromagnetism, where there is no question of collective modes, because there are no continuous degrees of freedom to support them.
Even though H does not obey full rotation group symmetry, the underlying dynamical object do: they are spins, a consequence of the rotation group properties of the fundamental particles, only coupled together and to a lattice in such a way as not to exhibit their full symmetry. Nonetheless, the group generators play a role in their excitation spectrum, and it is easy to deduce from that the underlying objects.
Spin waves
Phonons
Near a second-order Tc, no matter what the dimensioality and symmetry, there will be the finite temperature equivalent of zero-frequency modes, namely critical fluctuations with divergent amplitude as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow Tc}
. One imagines the coarse-grained average of the order parameter to be specified as a (necessarily very slowly varying) function of position: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M}=\mathbf{M}(\mathbf{r})}
, and then asks for the free energy as a functional of this functio, i.e., with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M}(\mathbf{r})}
constrained. It is clear that if an analytic expression exists near Tc for such an F, it must be approximated as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\alpha (T-Tc)M^2 + A(\nabla M)^2 + BM^4 +...}
in close analogy to the observatio about the energy at T=0 and also to the Landau free energy of a ferroelectric. The (T-Tc) term is the simplest way to ensure that M will grow from zero aboe Tc to a finite value below it. Then the probability of a fiben fluctuation M(r) will be
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P \propto e^{-\frac{F(M)}{T}}}
which leads to fluctuatio amplitudes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle M^2(k) \rangle = \frac{\langle M^2 e^{- F/T} \rangle}{\langle e^{-F/T} \rangle} \propto \frac{1}{\alpha (T-Tc) + Ak^2}}
which in turn diverges as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \rightarrow 0}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow Tc}
. This divergence in the fluctuation amplitudes in turn implies that the relevant frequencies approach zero in some manner.
The fluctuation of the last equation do become of quasimacroscopic size and dimension at the critical point, as a consequence of the divergences predicted. These fluctuations may or may not correspond to real collective modes. In the case of a continuous symmetry group, the low frequency collective excitations, which are necessarily there at absolute zero, are also present through out the temperature range up to Tc and merge, more or less, with the critical fluctuatio spectrum near Tc.
Phonons in solids and the spin waves are examples of "collisionless" modes, essentially quantum excitations required by the symmetries, or the conservation laws in some cases, of the system. But at frequencies low compared to microscopic relaxation times, these may merge into "hydrodynamic" modes, which have the character of ordinary sound waves, compressional or other modes of vibration in which the matter remains in local thermodynamic equilibrium.
The nature of the low-temperature collisionless excitations is more interesting in the much more common case in which the order parameter is not a constant of the motion, and in which the low-temperature state does not belong to a representation of the symmetry group of the Hamiltonian. A familiar example is the crystalline state.
crystalline state.
The plasma modes as a collisionless excitation is universal in charged condensed systems. For instance, it occurs in two important cases: the Wigner lattice, where only the two transverse modes behave as phonons, with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w \propto q}
, and the superconductor, where there are no Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w \rightarrow 0}
modes. In all cases, the zero-point motions of these collective modes play an important role in the energy and wave function of the ground state itself. The zero-point motion is central to the problem of restoring the broken symmetry
Generalized "rigidity"
When we move one end of a ruler, the other moves the same distance, such action at a distance is not built into the laws of nature except in the case of the long-range forces such as gravity or electrostatics. It is strictly a consequence of the fact that the energy is minimized when symmetry is broken in the same way throughout the sample: the phase and angle variables want to be uniform, so that the orientation and position of the lattice is the same everywhere. Of course, in general they are not quite the same, since the lattice can deform elastically, but nonetheless the lattice transmits that force from one end to the other even in equilibrium and without having to flow constantly like a viscous liquid. To break down the rigidity completely, we must supply the condensation energy of a macroscopic piece of the sample, which is very large.
The generalization of this concept to all of the instances of broken symmetry is it call here generalized rigidity. For instance, permanent magnets are so because the magnetization cannot change a little at a time. Superconductivity is the phase rigidity of the electron pair fluid.
Defect structures
There is a general rule that the breakdown of the generalized rigidity property, along with the resulting dissipation, is a consequence of the formation and motion of defect structures which are usually macroscopic in size.
The twin models for such effects are the domain theory of ferromagnetism, due to Landau (1941), Block (1930) and others, and the dislocation theory of G. I. Taylor (1934), Burgers (1939, 1940), and others. These two cases demonstrate nicely the one general statement which will be justified by the topological theory: that a one-dimensional order parameter allows only two-dimensional ("wall") defects; and that a two-dimensional order parameter allows linear defects such as dislocations, but not necessarily always; while a three- or more- dimensional case may allow point defects.
Clearly in any broken-symmetry system we can imagine forces which would disorient the order parameter in one region relative to another. As a simple example could be that different parts of the sample may have grown with different order parameters and eventually meet in the middle. In what ways can the system respond?
The most obvious and simplest is a boundary or "domain wall" (see next figure): one simply has two or more regions. each locally homogeneous, separated by boundaries. In the case of the one-dimensional order parameter, there is only a discrete set of local equilibrium states (directions of M for a ferromagnet, for instance, or of P for ferroelectric), and there must be a two-dimensional boundary (for a 3D sample) shape of the boundary or other singularity is determined by competition between the forces of generalized rigidity. In the boundary case, characteristically the wall is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx}
one lattice constant thick-- essentially, there is no length parameter except the fundamental microscopic length. Thin boundaries cannot move continuously in space --they are located at a specific crystal plan and must overcome an activation energy to move to the next.
In general, the response to external forces tending to twist or reverse the magnetization must in the first instance come from the motion of these boundaries. To make a permanent magnet, one can proceed in two ways: either to pin the existing boundaries, i.e., to make a very impure material, or to remove them, i.e., to make i of very small particles. Thus the response properties of magnets are wholly conditioned by the defect structures. This is, in fact, the general case.
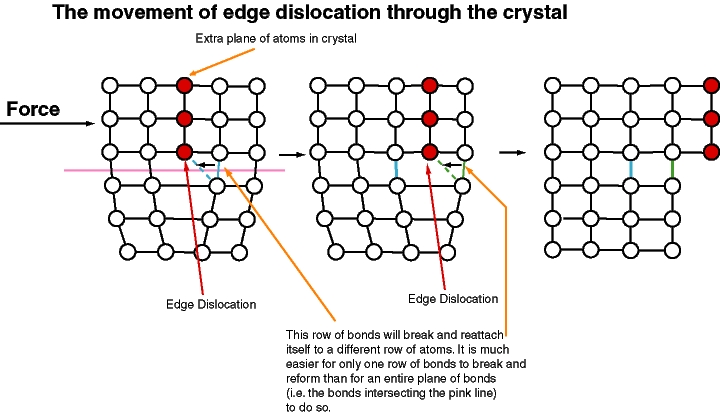
A second type of defect is a line defect. An example is the dislocation (see next figure). We can imagine following a closed path through a crystal along which the local phase varies gradually, corresponding to a small local strain, but then returns to the original phase changed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi}
. There must be associated a line of singularity where the lattice structure is essentially destroyed.
The two basic types of dislocations are edge dislocations, where an extra plane of atoms has been interpolated ending at a line singularity; and screw dislocations, where the lattice has the topology of a screw.
The easiest way in which a crystal can continuously slide against itself is by the continuous flow of dislocations across a line between the two. Again, there are two ways to make a strong crystal: the easy way is to pin the dislocations, one version of which is called work hardening; the hard way is to eliminate them altogether as in a "whisker" crystal.