Phy5670

Welcome to the Quantum Many Body Physics PHY5670 Fall2010

PHY5670 is a one semester graduate level course. Its aim is to introduce basic concepts, and logical framework, of this vast and developing discipline: broken symmetry and adiabatic continuity. Theoretical techniques, such as coherent state path integrals and diagrammatic perturbation expansions, will be used to emphasize these deeper underlying concepts, as well as to provide practical means of calculations. Few illustrative physical systems and quantum many-body models will also be studied.

The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.

Team assignments: Fall 2010 student teams

---

Outline of the course:

Conceptual basis of many body physics

Broken symmetry

What is broken symmetry?

Our experience shows us, then, that as matter cools down it usually no longer retains the full symmetry of the basic laws of quantum mechanics which it undoubtedly obeys; our task here is to understand that the questions we must ask are "Why", "In what sense", and "What are the consequences?" P.W. Anderson (Basic Notions of Condensed Matter Physics)

A system of particles can be mathematically described by its Hamiltonian, which considers the different interactions between the particles. Different systems can present many types of symmetries, e.g. translational or rotational symmetry. Whenever a system is found in a state that is less symmetric than the Hamiltonian describing that system, we say this symmetry is broken. Knowledge about the underlying symmetries of a system is essential for a mathematical description.

There is an essential difference between the statements a symmetry is broken and a symmetry is absent. Even a symmetry that is broken is of crucial importance to the phenomenology of the system, since the Hamiltonian still exhibits the symmetry. For example, a system of Ising spins at zero external field undergoes a second order phase transition to a ferromagnet state when it is cooled below the Curie-Temperature. In contrast, if an external field, explicitly breaking the symmetry between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow } configurations, is applied to the system, the transition is first order.

Translation broken symmetry. The red balls simulate a snapshot in a specific moment of a 2D system with isotropic density, where the possibility to find a particle in a specific place is homogeneous for all the space. The blue balls simulate the same system in a crystal configuration (with small thermal fluctuations) where the possibility to find a particle is higher in the lattice position.

Typical symmetries that are important for many-body systems are translational symmetry, rotational symmetry, time-reversal symmetry or gauge symmetries. Translational symmetries are broken when a system crystallizes. (The probability to find a particle at a specific location is not longer constant, instead it is a function displaying peaks at the locations corresponding to the lattice points). Rotational symmetry or isotropy is broken for example in liquid crystals, where the constituting molecules are non-spherical and align with each other, thus choosing a preferred direction for the macroscopic system. Gauge symmetries are broken in superconductors or superfluids, where bosons condensate into a single phase, and time-reversal symmetries are spontaneously broken for example by ferromagnets with aligned spins.

A transition between states of different symmetry is automatically a phase transition (but not each phase transition is accompanied by a broken symmetry). Obviously, systems in different symmetry states cannot be treated with the same ideas. Therefore it is crucial to define the symmetries of a given system before engaging in calculations.

Obviously the temperature of the system is a crucial factor, which define the internal energy. At very high temperatures the thermal fluctuations dominate over any kind of interaction and as result we could expect that all the symmetries will be present at some enough temperature and as the system cools down we would see the different broken symmetries. The many-boy theory pursue the description of the consequences of precisely these broken symmetries and in the next sections we will develop the theory that so far have been an efficient tool to describe many phenomenons.

Just to reflect the importance of the study of the broken symmetries and its consequences we could mention the work done by Yoichiro Nambu, Makoto Kobayashi and Toshihide Maskawa; which give them the Nobel prize in physics in 2008 "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature."

"Why" broken symmetry?

Some crystal structures of 3D systems.

Under surprisingly general circumstances the lowest energy state of a system does not have the total symmetry group of its Hamiltonian, and so in the absence of thermal fluctuations the system assumes an unsymmetrical state. P.W. Anderson (Basic Notions of Condensed Matter Physics)

While each system exhibits different symmetries and symmetry breaking, a general rule of thumb is that broken symmetries are to be expected whenever the potential energy in a system dominates the kinetic energy. In reverse, symmetries can be restored by going to higher temperatures (raising the kinetic energy).

The essential phenomenon is either case is that the lowest state of a potential energy of interaction between the particles -- for example, a pair interaction

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{tot}=\sum_{i<j}V(| r_i-r_j|)} -- must occur for either a unique relative configuration of all particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{r_1,r_2,\ldots r_N\}} and all translations and rotations,

or, in artificial cases, perhaps for a highly restricted subset of all configurations. P.W. Anderson (Basic Notions of Condensed Matter Physics)

The different crystal configurations that have been observed are the manifestation of precisely this point. Each system with its different interactions coalesces into different lattice arrangements at low temperature, when the potential energy dominates. As example we have the Wigner crystal that presents a crystal configuration with Coulombic interactions of its particles (see the next section of examples to more details).

It is then clear that in any situation where the potential energy dominates kinetic energy and entropy, as in the two cases mentioned, a system of particles obeying a simple potential will take up a regular lattice structure. P.W. Anderson (Basic Notions of Condensed Matter Physics)

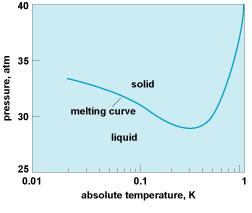
The less symmetric state tends to be one lower in temperature, simply because the more symmetric one is usually a distribution of thermal fluctuations among all the available values of the order parameter . But this order of phases is not a general rule; He3, for instance, violates it because the solid has a greater nuclear paramagnetic entropy than liquid, and at low temperatures the melting curve has a negative slope. So in this temperature regime, the solid is the high-temperature phase and the liquid is the low-temperature phase. P.W. Anderson (Basic Notions of Condensed Matter Physics)

The example of He3, and the underlying reason for its atypical behavior will be discussed below.

Symmetry breaking and the thermodynamic limit

This is a classical curve for the magnetization of a ferromagnet system where the magnetic field h=0

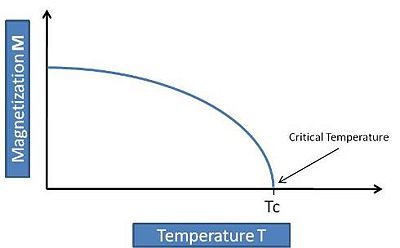
The transition between states of different symmetry can be characterized in terms of an order parameter, which is defined (in the sense of Landau) as any parameter that is zero in the symmetric phase (disordered phase) and non-zero in the broken symmetry phase (ordered phase). An example is the magnetization in a ferromagnet that is zero above a critical temperature Tc and finite, different than zero, for T<Tc (see figure). Note that there can be various different choices for the order parameter of a system. In a crystal, the density Fourier components corresponding to reciprocal lattice vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\vec{G}} } is an order parameter as well as the shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau } .

In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter since it is forced to zero by virtue of the symmetry.

The non-analyticity of the free energy at the phase transition is only possible in the thermodynamic limit, i.e. for systems with infinite number of particles. The reason behind this is that any finite sum over the analytic functions describing the contribution to the free energy of each particle will again be analytic. However, an infinite sum of analytic functions can be non-analytic, very much like it a non-analytic step function can be expressed as the sum of an infinite Fourier sum over analytic trigonometric functions.

Another way to see the necessity of the thermodynamic limit is by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system is initially in an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \downarrow } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \uparrow} . In order to minimize energy, the spins will realign. However, the return to the initial Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state is just as likely as the transition to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } . Over time, the system will be found in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state just as often as in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } state, and the overall magnetization will be zero. This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped simultaneously in order for the system to go from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \uparrow \uparrow \ldots } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \downarrow \downarrow \ldots } , and the typical time span the system needs to change from one ground state into another grows. For a system with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\infty } , ergodicity is broken, because even if each ground state is in principle equally likely, the system will stay in its initial state forever.

Of course, no real ferromagnet, crystal or other experimental system is truly infinite. However, typical macroscopic system sizes of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=10^{23}} are enough to make the lifetime of any initial ground state longer than the age of the universe. The system is frozen into one particular ground state; the symmetry connecting different ground states is dynamically broken.

By reversion of this argument, it is easy to see that no spontaneous symmetry breaking is possible in any microscopic system, such as molecules.

Many phase transitions that exhibit symmetry breaking are second order or continuous phase transitions. Examples are ferromagnets, antiferromagnets or superconductors. Second order phase transitions do not - in contrast to first order phase transitions - involve latent heat. An example of a first order phase transition with symmetry breaking is the liquid-to-solid-transition. The transition from liquid to gas is also of first order, but involves no symmetry change.

The distinction between phase transitions with and without symmetry breaking is very important, since the phenomena that can occur in each state are dictated by the symmetry exhibited. For example, it is only possible to get from one phase into another without crossing a phase border if both phases exhibit the same symmetry (as liquid and gaseous water), while phases with different symmetries are necessarily disjoint. These issues will be discussed in more detail in chapter 1.1.2.

Examples

Wigner Crystals

At low density, electrons in the jellium model crystallize into a bcc Wigner crystal. At high density (and sufficiently finite temperature) they behave as Fermi gas/liquid with all the invariance properties of the ordinary Boltzman gas, which this system is when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>>E_F} .

He 3

The melting curve of He3 at low temperature from E. R.Grilly, J. Low Temp. Phys., 11:33–52, 1973. Note that for a range of pressures, the solid He3 melts upon cooling(!). The reason behind such anomaly has its origin in solid having a greater paramagnetic entropy than (Fermi) liquid.

Diagram phase of Helium-3 from http://ltl.tkk.fi/research/theory/helium.html

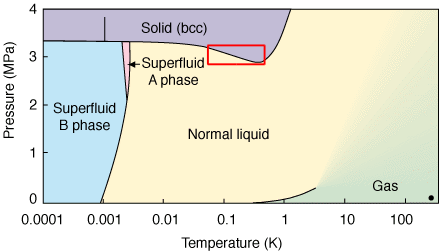
If we compress a high enough density Fermi liquid with short range repulsive interactions, approximately as He-3, it will form a regular solid. Helium-3 is an isotope that has only two protons and one neutron and it has different properties than helium-4 because the helium-3 is a fermion's system since the number of spins that it has, instead of the helium-4 which is a boson's system. Therefore He-3 should obey the Pauli exclusion principle. He-3 and He-4 have very interesting properties, for example that they solidified at very high pressures, since the weak interactions between their particles. Also to observed the liquid phase would be necessary very low temperatures (as we can appreciate in the phase diagram).

At very low temperatures and pressures it could be possible to observe a superfluid phase in the He-3. To explain this phase we can use the concept of broken symmetry that we have been talking about. He-3 has nine degrees of freedom from the spin and orbital rotations; and also there is the gauge invariance. From this we know that the order parameter should be a complex matrix of 3x3.

Actually the superfluidity of He-3 present two different phases discovered in 1970's. These phases are called A-phase and B-phase. In the B-phase the angular momentum and spin are isotropic and the total angular momentum is J=S+L=0. In the A-phase the spin and angular momentum are anisotropic.

Many properties of He-3 have been predicted using the theory of broken symmetry, even though the order parameter is very complicated because the many degrees of freedom.

other examples

In the next chart we show and compare different systems that exhibit broken symmetry.

---

Example	Disordered Phase	Ordered Phase	Order Parameter	Is the order parameter a constant of motion?
Ferromagnetism	Paramagnet	Ferromagnet	Magnetization M	Yes
Antiferromagnetism	Paramagnet	Antiferromagnet	Sublattice magnetization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{sl}}	No
Superconductivity	Normal Metal	Superconductor	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \Psi_{\sigma}^*, \Psi_{-\sigma}^*\rangle }	No
Crystal	Liquid	Solid	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\vec{G}}} , shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau}	No
He 3	Normal liquid	Anisotropic superfluid	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ij}=<\Psi\Psi>_{M_L,M_S}}	No

Note: To see more details and another phenomenons you can check "P.W. Anderson(Basic Notions of Condensed Matter Physics), pg.68"

As we can imagine there are just few examples were the order parameter is a constant of motion. The Ferromagnetism is one them, where we can take the order parameter as the total spin in some direction, but this is not a common case.

"What are the consequences?" of broken symmetry

• Discreteness of phase transitions, and the resulting failure of continuation: disjointness of physical phases
• Development of collective excitations
• Generalized rigidity
• Defect structures: dissipation and topological considerations

Discreteness and Disjointness

First theorem "It is impossible to change symmetry gradually. A given symmetry element is either there or it is not; there is no way for it to grow imperceptibly" (Landau and Lifshitz, 1958)

Phase diagram of water. We can appreciate the critical point "CP" in the diagram which can be surrounded in a "smooth" path to pass from liquid to vapor (or vice versa). This tell us that in the change of liquid to vapor there is not broken symmetry

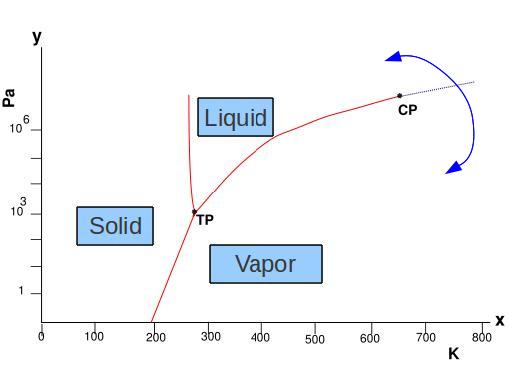
Let's analyze the phase diagram of the water (see figure above). As we can see in the diagram we can go from vapor to liquid in a "smooth path" just going around the critical point, actually this means that these two phases doesn't present a broken symmetry. On the other hand, it's impossible to go from liquid to solid smoothly (or in opposite way). The liquid-gas transition is typical of a symmetry-nonbreaking transition. There is no possibility that the fluid and gas can be in equilibrium at the same density except at a point on the boiling curve.

In the cases of true broken symmetry, the unsymmetrical state is normally characterized by and "order parameter". By Landau's definition this is simply any parameter that is zero in the symmetric state and has a nonzero average uniquely specifying state when the symmetry is broken; it is an additional variable necessary to specify the microscopic state in the lower symmetry state. Thus by broken symmetry a new variable is created. For example, in a nonmagnetic material the order parameter is the magnetization M, which in the absence of a magnetic field is zero by time-reversal symmetry and the state is specified by the usual intensive variables P and T.

It is possible to predict that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = -T \ln{<e^{-\beta H}>}} in the new system is a new mathematical function from than in the old. For instance, call the new variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Then in general we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = F(V,T,\psi)}

We calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = F(V,T)} by appending to this the equilibrium condition

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial F}{\partial \psi} = f = 0 }

where f is the generalized force variable (like the magnetic field H) corresponding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Above the critical temperature Tc, this is satisfied by symmetry; below, it is nontrivial. Then from the las two equations the result is a new function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F'(V,T) } , which is not analytic at Tc. This is Landau's essential insight.

In simplest terms, it is quite clear that the First Theorem requires that F have a boundary of singularities between the two regimes of symmetry, and that therefore analytic continuation between the two is not possible.

Generalized "rigidity"

When we move one end of a ruler, the other moves the same distance, such action at a distance is not built into the laws of nature except in the case of the long-range forces such as gravity or electrostatics. It is strictly a consequence of the fact that the energy is minimized when symmetry is broken in the same way throughout the sample: the phase and angle variables want to be uniform, so that the orientation and position of the lattice is the same everywhere. Of course, in general they are not quite the same, since the lattice can deform elastically, but nonetheless the lattice transmits that force from one end to the other even in equilibrium and without having to flow constantly like a viscous liquid. To break down the rigidity completely, we must supply the condensation energy of a macroscopic piece of the sample, which is very large.

The generalization of this concept to all of the instances of broken symmetry is it call here generalized rigidity. For instance, permanent magnets are so because the magnetization cannot change a little at a time. Superconductivity is the phase rigidity of the electron pair fluid.

Defect structures

Movement of dislocation from http://www.ic.arizona.edu/ic/mse257/class_notes/disclocation.html

There is a general rule that the breakdown of the generalized rigidity property, along with the resulting dissipation, is a consequence of the formation and motion of defect structures which are usually macroscopic in size.

The twin models for such effects are the domain theory of ferromagnetism, due to Landau (1941), Block (1930) and others, and the dislocation theory of G. I. Taylor (1934), Burgers (1939, 1940), and others. These two cases demonstrate nicely the one general statement which will be justified by the topological theory: that a one-dimensional order parameter allows only two-dimensional ("wall") defects; and that a two-dimensional order parameter allows linear defects such as dislocations, but not necessarily always; while a three- or more- dimensional case may allow point defects.

Clearly in any broken-symmetry system we can imagine forces which would disorient the order parameter in one region relative to another. As a simple example could be that different parts of the sample may have grown with different order parameters and eventually meet in the middle. In what ways can the system respond?

We can appreciate how the domain wall separate the two magnetic domains in the system.

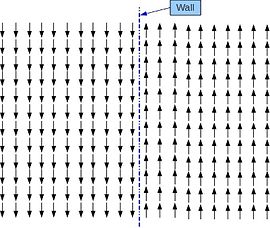
The most obvious and simplest is a boundary or "domain wall" (see right figure): one simply has two or more regions. each locally homogeneous, separated by boundaries. In the case of the one-dimensional order parameter, there is only a discrete set of local equilibrium states (directions of M for a ferromagnet, for instance, or of P for ferroelectric), and there must be a two-dimensional boundary (for a 3D sample) shape of the boundary or other singularity is determined by competition between the forces of generalized rigidity. In the boundary case, characteristically the wall is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx} one lattice constant thick-- essentially, there is no length parameter except the fundamental microscopic length. Thin boundaries cannot move continuously in space --they are located at a specific crystal plan and must overcome an activation energy to move to the next.

In general, the response to external forces tending to twist or reverse the magnetization must in the first instance come from the motion of these boundaries. To make a permanent magnet, one can proceed in two ways: either to pin the existing boundaries, i.e., to make a very impure material, or to remove them, i.e., to make i of very small particles. Thus the response properties of magnets are wholly conditioned by the defect structures. This is, in fact, the general case.

Line defect from http://www.tf.uni-kiel.de/matwis/amat/def_ge/kap_5/illustr/dislocation_3dim.jpg.

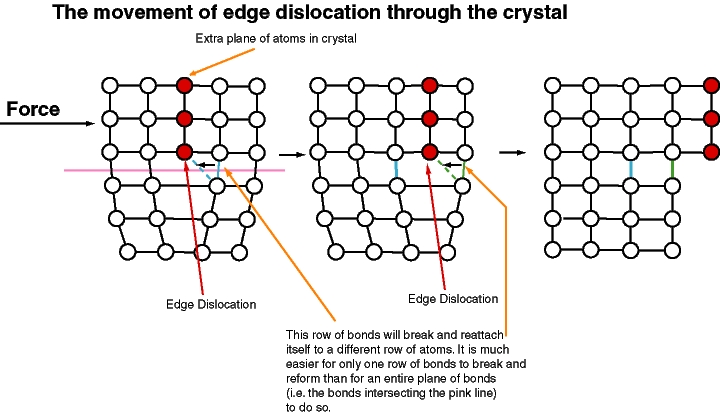
A second type of defect is a line defect. An example is the dislocation (see next figure). We can imagine following a closed path through a crystal along which the local phase varies gradually, corresponding to a small local strain, but then returns to the original phase changed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} . There must be associated a line of singularity where the lattice structure is essentially destroyed.

The two basic types of dislocations are edge dislocations, where an extra plane of atoms has been interpolated ending at a line singularity; and screw dislocations, where the lattice has the topology of a screw.

The easiest way in which a crystal can continuously slide against itself is by the continuous flow of dislocations across a line between the two. Again, there are two ways to make a strong crystal: the easy way is to pin the dislocations, one version of which is called work hardening; the hard way is to eliminate them altogether as in a "whisker" crystal.

Collective excitations

The Hamiltonian describing the internal interactions in a macroscopic system still obeys the initial transformations of the symmetry group. The state, however, does not. Immediate consequences of this are

A) The dynamics and character of elementary excitations is given almost exclusively by this information.

B) There exist new static properties in the broken-symmetry phase that we can call generalized "rigidity". (Described in detail above)

C) Order parameter defects. (Described in detail above)

There are two cases of consequence A:

Case 1) The new broken symmetry state is an eigenstate of the Hamiltonian. (The order parameter is a constant of the motion).

e.g. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -J\sum_{<i,j>}\vec{S_i}\cdot\vec{S_j} }  : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle < \vec{S_{tot}} > \neq 0 } in ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S_{tot}} = \sum_{i=1}^{N}\vec{S_i} }

Case 2) The new broken symmetry state is not an eigenstate of the Hamiltonian. (The order parameter is not a constant of the motion).

e.g. A crystal cannot be an eigenstate of the Hamiltonian. Positions are fixed, and thus will not commute with the kinetic energy operator.

In Case 1) Spin waves disperse quadratically with momentum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega ~ k^2 } In Case 2) Spin waves disperse linearly with momentum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega ~ k }

There tend to be more examples of case 2, such as crystals, antiferromagnets, nematics (liquid crystals), etc.

Phonon

For discrete atoms, one can construct waves of different wavelengths and speeds that all corresponds to a wave inside 1st Brillouin zone, from a single mode of vibration. author : Lee, Sunhyu (wikipedia ID : shaind)

At low enough temperatures, matter does not obey the initial symmetry, which the Hamiltonian of the system does. From this fact, one of the most important and interesting properties of matter appears that is the state of elementary excitations and fluctuations. The new state can be either an eigenstate of Hamiltonian or not.

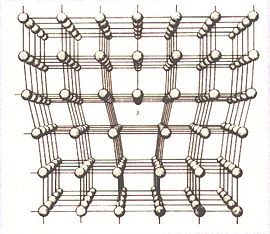
As stated earlier, a crystal cannot be an eigenstate of the Hamiltonian. The excitations of vibrational modes in crystal are represented by phonons. A phonon is a description of a special type of vibrational motion, in which a lattice uniformly oscillates at the same frequency i.e. normal modes. Thereby, phonon is a quantum notion of normal modes. These normal modes are important because any arbitrary lattice vibration can be considered as a superposition of these elementary vibrations.

The name phonon comes from the Greek word φωνή (phonē), which translates as sound, because long-wavelength phonons give rise to sound.

To learn more about these vibrational excitations, consider the Hamiltonian which ground state is a cubic crystal:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{j=1}^N {p_j^2 \over 2m} + \sum_{i>j}V (\mathbf{r_i} -\mathbf{r_j})\ } .

With this Hamiltonian, we will make two assumptions:

1. We assume that the mean equilibrium position of each ion is a Bravais lattice site. We associate with each ion a particular Bravais lattice site R, about which the ion in crystal oscillates.

2. Assuming that the typical displacement of each ion from its equilibrium position are small compared with the interionic spacing.

Assumption 1 makes the Bravais lattice still there in spite of ionic motion, but the lattice describes the average ionic configuration rather than the instantaneous one. One thing to be remembered, although this assumption permits a wide range of possible ionic motion, it does not allow for ionic diffusion: The oscillation of each ion are assumed to be forever about a particular lattice.

Assumption 2 will lead to the harmonic approximation theory. The results of this theory are often in agreement with observed properties of solid. But, some properties still can not be explained by harmonic theory, and one has to go to anharmonic theory to account for those properties.

From assumption 1, we denote the position of the ion whose mean position is R by r(R). In reality, r(R) will deviate from its average value R, and we can write at any given time:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}(\mathbf{R})=\mathbf{R}+\mathbf{u}(\mathbf{R})} ,

where u(R) is the deviation from equilibrium of the ion whose equilibrium site is R and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}=a(l\hat{x}+m\hat{y}+n\hat{z})} ,

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is lattice constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,m,n} are integers.

Hamiltonian above assumes that a pair of atoms separated by r contributes an amount of potential energy U(r). Then, we can write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}{2}\sum_{RR'}V(\mathbf{r(R)-r(R')})=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .

Hence the potential energy now depends on the dynamical variables u(R).

For kinetic energy term, we make substitution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{p}_{j}\rightarrow \mathbf{P(R)} } .

Then, we have Hamiltonian:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{R}{P(\mathbf{R})^{2} \over 2M}+\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .

Now coming the role of assumption 2, we make approximation based on the expectation that the atoms will not deviate substantially from their equilibrium positions. If all the u(R) are small, then we can expand the potential energy V about its equilibrium position using Taylor's expansion,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf{r+a})=f(\mathbf{r})+\mathbf{a}.\nabla f(\mathbf {r})+\frac{1}{2!}(\mathbf{a}.\nabla)^{2}f(\mathbf{r})+\frac{1}{3!}(\mathbf{a}.\nabla)^{3}f(\mathbf{r})+...} .

Applying this expansion to each term in the potential energy, with r = R - R' and a = u(R) - u(R'), we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})=&\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})+\frac{1}{2}\sum_{RR'}(\mathbf{u(R)-u(R')}).\nabla V(\mathbf{R-R'})\\ &+\frac{1}{4}\sum_{RR'}[(\mathbf{u(R)-u(R')}).\nabla]^{2}V(\mathbf{R-R'})+...\\ \end{align}}

The coefficient of u(R) in the linear term above is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{R'}\nabla V(\mathbf{R-R'})} .

This is just minus the force exerted on the atom at R by all other atoms, when each is placed at its equilibrium position. Therefore, it must vanish because there is no net force on atoms in equilibrium.

Then, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=U^{eq}+U^{harm}} ,

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{eq}=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})}

and

$U^{harm}={\frac {1}{4}}\sum _{\mathbf {RR'} }[\mathbf {u_{\mu }(R)-u_{\mu }(R')} ]\phi _{\mu \nu }[\mathbf {u_{\nu }(R)-u_{\nu }(R')} ]$,

$\phi _{\mu \nu }(\mathbf {r} )={\partial ^{2}V(\mathbf {r} ) \over \partial r_{\mu }\partial r_{\nu }}$

Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{eq}} is just a constant (i.e., independent of the u's and P's), it can be ignored in many dynamical problems, and one frequently acts as if the total potential energy were just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}} , dropping the superscript altogether when no ambiguity is likely to result.

The harmonic approximation is the starting point for all theories of lattice dynamics. Further corrections to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} , especially those of third and fourth order in the u's, are known as anharmonic terms, and are of considerable importance in understanding many physical phenomena. They are generally treated as small perturbations on the dominant harmonic term.

The harmonic potential energy is usually written in the more general form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}=\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{\mu \nu}(\mathbf{R-R'})=\delta_{\mathbf{R,R'}}\sum_{\mathbf{R''}}\phi_{\mu \nu}(\mathbf{R-R''})-\phi_{\mu \nu}(\mathbf{R-R'})} .

Then, the harmonic Hamiltonian becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{harm}=\sum_{\mathbf{R}}\frac{1}{2M}P(\mathbf{R})^{2}+\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}

We will extract the eigenvalues from this Hamiltonian. Later, we will find that the energy of an N-ion harmonic crystal can be regarded as from 3N discrete normal modes. These discrete normal modes are the quasi-particles called phonons.

We proceed as following. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} be the frequency and polarization vector for the classical normal mode with polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} and wave vector k. We now define the "phonon annihilation operator"

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k.R}}\mathbf{\epsilon}_{s}(\mathbf{k}).\left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}+i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{P(R)}\right]} ,

and its adjoint, the "phonon creation operator"

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k.R}}\mathbf{\epsilon}_{s}(\mathbf{k}).\left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}-i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{P(R)}\right]} .

The canonical commutation relations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),P_\nu (\mathbf{R'})]=i\hbar\delta_{\mu\nu}\delta_\mathbf{R,R'}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),u_\nu (\mathbf{R'})]=[P_\mu (\mathbf{R}),P_\nu (\mathbf{R'})]=0} ,

the identity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{R}e^{i\mathbf{k.R}}=\begin{cases}0,\quad\quad\quad&\mathbf{k}\quad is\quad not\quad a\quad reciprocal\quad lattice\quad vector,\\ N,&\mathbf{k}\quad is\quad a\quad reciprocal\quad lattice\quad vector,\end{cases}}

and the orthonormality of polarization vectors

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon_s(k).\epsilon_{s'}(k)}=\delta_{ss'}, \quad \quad s,s'=1,2,3}

yield the commutation relations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&[a_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=\delta_\mathbf{kk'}\delta_{ss'},\\ &[a_{\mathbf{k}s},a_{\mathbf{k'}s'}]=[a^\dagger_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=0.\end{align}}

One can express the coordinates and momenta in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&\mathbf{u(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar \over 2M\omega_s(\mathbf{k})}(a_{\mathbf{k}s}+a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k.R}},\\ &\mathbf{P(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar M\omega_s(\mathbf{k})\over 2}(a_{\mathbf{k}s}-a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k.R}}.\end{align}}

Equation above can be obtained by substitution of equations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}} , and by use of the "completeness relation" that holds for any complete set of real orthogonal vectors,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{s=1}^3[\mathbf{\epsilon}_s(\mathbf{k})]_\mu[\mathbf{\epsilon}_s(\mathbf{k})]_\nu=\delta_{\mu\nu},}

together with identity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{k}e^{i\mathbf{k.R}}=0,\quad\quad \mathbf{R}\neq 0.}

We already expressed u(R) and P(R) in terms of annihilation and creation operators. Thereby, we can also write the harmonic Hamiltonian in terms of the new operators. It can be shown that the kinetic energy is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {1 \over 2M}\sum_\mathbf{R}\mathbf{P(R)}^2=\frac{1}{4}\sum_{\mathbf{k}s}\hbar\omega_s(\mathbf{k})(a_{\mathbf{k}s}-a^\dagger_{\mathbf{-k'}s'})(a^\dagger_{\mathbf{k}s}-a_{\mathbf{-k'}s'}).}

For potential energy, we define the dynamical matrix D(k)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}=\sum_\mathbf{R}\mathbf{D(R)}e^{-i\mathbf{k.R}}.}

It can be proven that polarization vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} are the eigenvectors of the dynamical matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2\mathbf{\epsilon}=\mathbf{D(k)}\mathbf{\epsilon}.}

Using these facts, we can write the potential energy as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}{4}\sum_{\mathbf{k}s}\hbar\omega_s(\mathbf{k})(a_{\mathbf{k}s}+a^\dagger_{\mathbf{-k'}s'})(a^\dagger_{\mathbf{k}s}+a_{\mathbf{-k'}s'}).}

Adding the kinetic and potential terms together, we get that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H={1 \over 2}\sum \hbar \omega_s(\mathbf{k})(a_{\mathbf{k}s}a^\dagger_{\mathbf{k}s}+a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}),}

and, using the commutation relations, we find that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H={1 \over 2}\sum \hbar \omega_s(\mathbf{k})(a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}+{1 \over 2}).}

This is nothing more than the sum of 3N independent oscillators, one for each wave vector and polarization. When a Hamiltonian divided into a sum of commuting sub-Hamiltonians, its eigenstates are simply all products of the eigenstates of sub-Hamiltonians, and the eigenvalues are the sum of the individual eigenvalues of the sub-Hamiltonians. We can therefore specify an eigenstate of H by giving a set of 3N quantum numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\mathbf{k}s}} , one for each of the 3N independent oscillator Hamiltonians Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\omega_s(\mathbf{k})(a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}+{1 \over 2})} . The energy of such a state is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\sum(n_{\mathbf{k}s}+{1 \over 2})\hbar\omega_s\mathbf{(k)}.}

In the corpuscular description the independent oscillators that give rise to normal modes can be regarded as quasiparticles i.e. phonons.

Spin Waves and the Heisenberg Ferromagnet

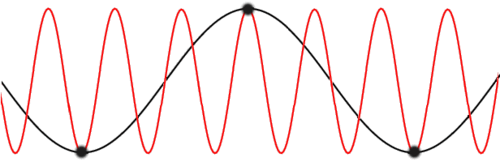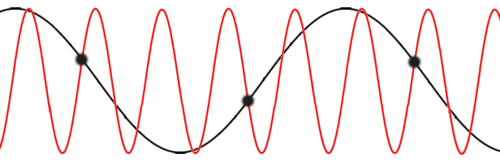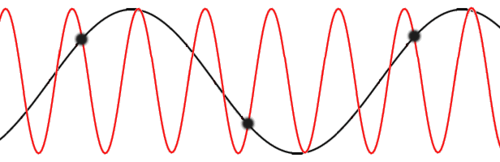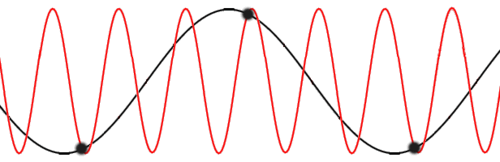
A spin wave (also called a magnon) is a collective magnetic excitation of an ordered ferromagnet. The projection of spin on an atom is reduced by one, but the excitation is not localized and propagates in the form of a wave throughout the lattice.

Spin waves can be derived by constructing a low lying excited state to an ordered ferromagnet. Assuming a cubic lattice, we can write the Hamiltonian for the isotropic (Heisenberg) ferromagnet as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J(R - R') } is short ranged, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J > 0 } . The ground state occurs when all of the spins are aligned. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S\rangle } is the maximum spin projection, then the ground state is : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0 \rangle = \prod_R |S\rangle_R}

Trying to lower a single spin to create an excited state eigenstate does NOT produce an eignestate. For example, we can create a state which is the same as the ground state, except the spin at R has been lowered:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle = \frac{1}{\sqrt{2S}}S^{-}(R)|0\rangle }

However, the Hamiltonian will flip the spin at R back up, and then flip another spin at R' down. First we rewrite the Hamiltonian, using the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{\pm}(R) = S^x(R)\pm iS^y(R)} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^x(R) \vec S^x(R') -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^y(R) \vec S^y(R') }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R) }

Now examine how this Hamiltonian acts on our proposed state:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|R_0\rangle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R')|R_0\rangle - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R)|R_0\rangle }

The first term (ignoring constants):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec S^z(R) \vec S^z(R')|R_0\rangle = \vec S^z(R) \vec S^z(R')\vec S^-(R_0)|0\rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R)\left( \left[S^{z}(R'),S^{-}(R_0) \right] + \vec S^{-}(R_0)\vec S^z(R') \right) |0\rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R) \left( -S^{-}(R_0)\delta_{R',R_0} + S S^{-}(R_0) \right) |0\rangle }

$=\delta _{R,R_{0}}\delta _{R',R_{0}}S^{-}(R_{0})|0\rangle -S\delta _{R',R_{0}}S^{-}(R_{0})|0\rangle -S\delta _{R,R_{0}}S^{-}(R_{0})+S^{2}S^{-}(R_{0})|0\rangle$

Now returning the constants: $-{\frac {1}{2}}\sum _{R\neq R'}J(R-R'){\vec {S}}^{z}(R){\vec {S}}^{z}(R')|R_{0}\rangle ={\frac {S}{2}}\sum _{R\neq R'}J(R-R_{0})|R_{0}\rangle +{\frac {S}{2}}{\frac {S}{2}}\sum _{R\neq R'}J(R_{0}-R')|R_{0}\rangle -{\frac {S^{2}}{2}}\sum _{R\neq R'}J(R-R')|R_{0}\rangle$

$=S\sum _{R\neq R'}J(R-R')|R_{0}\rangle +E_{0}$

Where the last term, E_0, is the ground state energy. So far $|R_{0}\rangle$ appears to be an eigenstate of the Hamiltonian. However, we much still examine the second term:

The second term: (ignoring constants)

$S^{-}(R')S^{+}(R)|R_{0}\rangle =S^{-}(R')S^{+}(R)S^{-}(R_{0})|0\rangle$

$=S^{-}(R')\left[S^{+}(R),S^{-}(R_{0})\right]|0\rangle$

$=S^{-}(R')\left(2S^{z}(R)\delta _{R,R_{0}}\right)|0\rangle =2S\delta _{R,R_{0}}S^{-}(R')|0\rangle$

Now returning the constants:

${\frac {1}{2}}\sum _{R\neq R'}J(R-R')S^{-}(R')S^{+}(R)|R_{0}\rangle =-S\sum _{R\neq R'}J(R-R')\delta _{R,R_{0}}|R'\rangle$

$=-S\sum _{R\neq R_{0}}J(R_{0}-R)|R\rangle$

Therefore, we have:

$H|R_{0}\rangle =E_{0}|R_{0}\rangle +S\sum _{R\neq R_{0}}J(R_{0}-R)\left(|R_{0}\rangle -|R\rangle \right)$

Therefore, $|R_{0}\rangle$ is not an eigenstate of the Hamiltonian. Although $|R_{0}\rangle$ is not an eigenstate, it is a linear combination of $|R_{0}\rangle$ and other states with one lowered spin.

So we must continue to seek and excited state eigenstate. Because J depends on R and R' only in a translationally variant combination, we can seek eigenstates of the form:

$|{\vec {k}}\rangle ={\frac {1}{\sqrt {N}}}\sum _{R}e^{i{\vec {k}}\cdot {\vec {R}}}|R_{0}\rangle$

This makes a superposition of phase factors of states where only one spin is flipped. Applying the Hamiltonian to this state yields:

$H|{\vec {k}}\rangle =E_{0}|{\vec {k}}\rangle +{\frac {S}{\sqrt {N}}}\sum _{R\neq R'}J(R-R')\left(e^{i{\vec {k}}\cdot {\vec {R}}}|R'\rangle -e^{i{\vec {k}}\cdot {\vec {R}}'}|R\rangle \right)$

---