Phy5670
Welcome to the Quantum Many Body Physics PHY5670 Fall2010
PHY5670 is a one semester graduate level course. Its aim is to introduce basic concepts, and logical framework, of this vast and developing discipline: broken symmetry and adiabatic continuity. Theoretical techniques, such as coherent state path integrals and diagrammatic perturbation expansions, will be used to emphasize these deeper underlying concepts, as well as to provide practical means of calculations. Few illustrative physical systems and quantum many-body models will also be studied.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments: Fall 2010 student teams
Outline of the course:
Conceptual basis of many body physics
Broken symmetry
As symmetries can heavily constrain the variables describing a system and often dictate the ansatz for a solution, their analysis is generally the first step taken dealing with a certain problem. The concept of broken symmetry, where the symmetry is less obvious (but nevertheless present) is a very powerful tool in Quantum Many Body physics as well as in many other fields. One example is High energy physics, where broken symmetries play a dominant role and one central effort is the search for the mechanism of electroweak symmetry breaking, whether it is the proposed Higgs particle or a more complex solution. In 2008, the Nobel prize in physics was awarded to one half to Yoichiro Nambu "for the discovery of the mechanism of spontaneous broken symmetry in subatomic physics". The other half went jointly to Makoto Kobayashi and Toshihide Maskawa "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature".
In the following, we will explain the concept of broken symmetries and highlight applications in many body physics.
What is broken symmetry?
Our experience shows us, then, that as matter cools down it usually no longer retains the full symmetry of the basic laws of quantum mechanics which it undoubtedly obeys; our task here is to understand that the questions we must ask are "Why", "In what sense", and "What are the consequences?" P.W. Anderson (Basic Notions of Condensed Matter Physics)

A system of particles is defined by its Hamiltonian which describes the different interactions between the particles. Different systems can present many types of symmetries, e.g. translational or rotational symmetry. Whenever a system is found in a state that is less symmetric than the Hamiltonian describing that system, we say this symmetry is broken. Knowledge about the underlying symmetries of a system is essential for a mathematical description.
There is an essential difference between the statements a symmetry is broken and a symmetry is absent. Even a symmetry that is broken is of crucial importance to the phenomenology of the system, since the underlying Hamiltonian still exhibits the symmetry. For example, a system of Ising spins at zero external field undergoes a second order phase transition to a ferromagnet state when it is cooled below the Curie-Temperature. In contrast, if an external field, explicitly breaking the symmetry between spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow} and spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow } configurations, is applied to the system the transition is first order.
Typical symmetries that are important for many-body systems are translational symmetry, rotational symmetry, time-reversal symmetry and gauge symmetries. When a system crystallizes, translational symmetries are broken. (The probability to find a particle at a specific location is not longer constant, instead it is a function displaying peaks at the locations corresponding to the lattice points). Rotational symmetry or isotropy is broken for example in liquid crystals, where the constituting molecules are non-spherical and align with each other, thus choosing a preferred direction for the macroscopic system. Gauge symmetries are broken in superconductors or superfluids, where bosons condensate into a single phase, and time-reversal symmetries are spontaneously broken for example by ferromagnets with aligned spins.
A transition between states of different symmetry is automatically a phase transition (but not each phase transition is accompanied by symmetry breaking). Many phase transitions that exhibit symmetry breaking are of second order or continuous phase transitions. Examples are ferromagnets, antiferromagnets or superconductors. Second order phase transitions do not - in contrast to first order phase transitions - involve latent heat. An example of a first order phase transition with symmetry breaking is the liquid-to-solid-transition. The transition from liquid to gas is also of first order, but involves no symmetry change.
The distinction between phase transitions with and without symmetry breaking is very important, since the phenomena that can occur in each state are dictated by the symmetry exhibited. For example, it is only possible to get from one phase into another without crossing a phase border if both phases exhibit the same symmetry (as liquid and gaseous water), while phases with different symmetries are necessarily disjoint. These issues will be discussed in more detail in chapter 1.1.2.
Obviously, systems in different symmetry states cannot be solved with the same approach. Therefore it is crucial to define the symmetries of a given system before engaging in calculations.
"Why" broken symmetry?
Under surprisingly general circumstances the lowest energy state of a system does not have the total symmetry group of its Hamiltonian, and so in the absence of thermal fluctuations the system assumes an unsymmetrical state. P.W. Anderson (Basic Notions of Condensed Matter Physics)
While each system exhibits different symmetries and different symmetry breaking patterns, a general rule of thumb is that broken symmetries are to be expected whenever the potential energy in a system dominates the kinetic energy. Reversely, symmetries can be restored by going to higher temperatures (raising the kinetic energy).
The essential phenomenon in either case is that the lowest state of a potential energy of interaction between the particles -- for example, a pair interaction
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle V_{tot}=\sum_{i<j}V(| r_i-r_j|)}
-- must occur for either a unique relative configuration of all particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{r_1,r_2,\ldots r_N\}} and all translations and rotations, or, in artificial cases, perhaps for a highly restricted subset of all configurations. P.W. Anderson (Basic Notions of Condensed Matter Physics)
When all particles have a "unique relative configuration", the system has crystallized. There is a finite number of possible lattice structures (some examples of 3 dimensional lattices are shown above). It is easy to see that these lattices only obey discrete symmetries (translation by a integer multiple of the lattice spacing, or rotations by certain fixed angles) instead of the contious rotational and translational symmetries of a gas or liquid.
It is then clear that in any situation where the potential energy dominates kinetic energy and entropy, as in the two cases mentioned, a system of particles obeying a simple potential will take up a regular lattice structure. P.W. Anderson (Basic Notions of Condensed Matter Physics)
The less symmetric state tends to be one lower in temperature, simply because the more symmetric one is usually a distribution of thermal fluctuations among all the available values of the order parameter . But this order of phases is not a general rule; 3He, for instance, violates it because the solid has a greater nuclear paramagnetic entropy than liquid, and at low temperatures the melting curve has a negative slope. So in this temperature regime, the solid is the high-temperature phase and the liquid is the low-temperature phase. P.W. Anderson ("Basic Notions of Condensed Matter Physics")
The example of 3He, and the underlying reason for its atypical behavior will be discussed below.
Symmetry breaking and the thermodynamic limit
The transition between states of different symmetry can be characterized in terms of an order parameter, which is defined (in the sense of Landau) as any parameter that is zero in the symmetric phase (disordered phase) and non-zero in the broken symmetry phase (ordered phase). An example is the magnetization in a ferromagnet that is zero above a critical temperature Tc and finite, different than zero, for T<Tc (see figure). Note that there can be various different choices for the order parameter of a system. In a crystal, the density Fourier components corresponding to reciprocal lattice vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \rho_{\vec{G}} } is an order parameter as well as the shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau } .
In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter (which is forced to zero by virtue of the symmetry).
The non-analyticity of the free energy at the phase transition is only possible in the thermodynamic limit, i.e. for systems with infinite number of particles. The reason behind this is that any finite sum over the analytic functions describing the individual contributions to the free energy of each particle will again be analytic. However, an infinite sum of analytic functions can be non-analytic. (For example, the non-analytic step function can be written as an infinite Fourier sum over analytic trigonometric functions.)
Another way to see the necessity of the thermodynamic limit is by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system initially is in an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \downarrow } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \uparrow} . In order to minimize energy, the spins will realign. However, the return to the initial Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state is just as likely as the transition to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } . Over time, the system will be found in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state just as often as in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } state, and the overall magnetization will be zero. This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped in order for the system to go from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \uparrow \uparrow \ldots } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \downarrow \downarrow \ldots } , and the typical time span the system needs to change from one ground state into another grows. For a system with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\infty } , ergodicity is broken, because even if each ground state is in principle equally likely, the system will stay in its initial state forever.
Of course, no real ferromagnet, crystal or other experimental system is truly infinite. However, typical macroscopic system sizes of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N=10^{23}} are enough to make the lifetime of any initial ground state longer than the age of the universe. The system is frozen into one particular ground state; the symmetry connecting different ground states is dynamically broken.
By reversion of this argument, it is easy to see that spontaneous symmetry breaking is impossible in any microscopic system, such as molecules.
Examples
Wigner Crystals
A uniform gas of electrons on a neutralizing background (jellium model) will crystallize if the electron density falls below a critical value. The reason is that at low densities the potential energy due to Coulomb interactions between electrons dominates over their kinetic energy. The existence of a crystalline phase was first predicted by Eugene Wigner in 1934. At zero temperature, the dimensionless Wigner-Seitz radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle r_s=a/a_B } characterizes the state of a uniform electron gas, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a } is the average inter-particle spacing and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a_B } is the Bohr radius. The critical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle r_s} , above which the system form a Wigner crystal, can be determined by quantum Monte Carlo simulations. The Wigner crystal is peculiar in the sense that in contrast to most other crystal it melts when the density is increased.
Wigner crystals of heavy ions have been postulated to exist inside of white dwarfs.
Helium-3
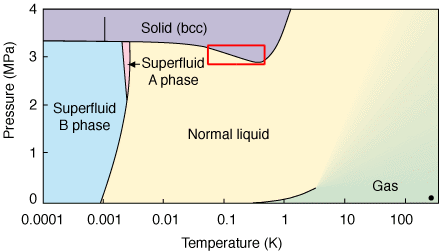
The Helium-3 isotope has two protons and one neutron. This makes He-3 a fermionic system subject to the Fermi exclusion principle. At very low temperatures, He-3 will crystallize, and therewith spontaneously break translational symmetry.
The phase diagram of He-3 displays a curiosity: there is a region where decreasing the temperature leads to a transitions from solid to liquid state (see the red square in the phase diagram above). Usually it is the other way around, the temperature has to be increased to go from solid to liquid phase (melting). While the opposite behavior in the case of He-3 looks paradoxical at first, it is in fact perfectly logical: Within the red square, the system has more entropy than the solid state than in the liquid state because of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^N } possible spin orientations in the crystal.
At very low temperatures and pressures it could be possible to observe a superfluid phase in the He-3. To explain this phase we can again use the concept of broken symmetry. The symmetries of He-3 are that of the spin and orbital rotations (9 degrees of freedom); and gauge invariance.
The superfluid He-3 presents intself in two different phases, discovered in 1970's. These phases are called A-phase and B-phase. In the B-phase the angular momentum and spin are isotropic and the total angular momentum is J=S+L=0. In the A-phase the spin and angular momentum are anisotropic. Therefore to pass from the B-phase to the A-phase angular momentum isotropy has to be broken.
Many properties of He-3 have been predicted using the theory of broken symmetry, even though the order parameter is very complicated because the many degrees of freedom. We can see that the theoretical concepts of quantum many body physics, in particular the concept of broken symmetry, have direct application to understand the behavior of real systems as the He-3.
Other examples
In the next chart we show and compare different systems that exhibit broken symmetry.
| Example | Disordered Phase | Ordered Phase | Order Parameter | Is the order parameter a constant of motion? |
| Ferromagnetism | Paramagnet | Ferromagnet | Magnetization M | Yes |
| Antiferromagnetism | Paramagnet | Antiferromagnet | Sublattice magnetization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{sl}} | No |
| Superconductivity | Normal Metal | Superconductor | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \Psi_{\sigma}^*, \Psi_{-\sigma}^*\rangle } | No |
| Crystal | Liquid | Solid | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\vec{G}}} , shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} | No |
| He 3 | Normal liquid | Anisotropic superfluid | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ij}=<\Psi\Psi>_{M_L,M_S}} | No |
Note: To see more details and another phenomenons you can check "P.W. Anderson(Basic Notions of Condensed Matter Physics), pg.68"
As we can imagine there are just few examples were the order parameter is a constant of motion. The Ferromagnetism is one them, where we can take the order parameter as the total spin in some direction, but this is not a common case.
Consequences of broken symmetry
- Discreteness of phase transitions, and the resulting failure of continuation: disjointness of physical phases
- Development of collective excitations
- Generalized rigidity
- Defect structures: dissipation and topological considerations
Discreteness and Disjointness
First theorem "It is impossible to change symmetry gradually. A given symmetry element is either there or it is not; there is no way for it to grow imperceptibly" (Landau and Lifshitz, 1958)
Let's analyze the phase diagram of the water (see figure above). As we can see in the diagram we can go from vapor to liquid in a "smooth path" just going around the critical point, actually this means that these two phases doesn't present a broken symmetry. On the other hand, it's impossible to go from liquid to solid smoothly (or in opposite way). The liquid-gas transition is typical of a symmetry-nonbreaking transition. There is no possibility that the fluid and gas can be in equilibrium at the same density except at a point on the boiling curve.
In the cases of true broken symmetry, the unsymmetrical state is normally characterized by an "order parameter". By Landau's definition this is simply any parameter that is zero in the symmetric state and has a nonzero average when the symmetry is broken. It is an additional variable necessary to specify the microscopic state in the lower symmetry state. Thus by breaking symmetry a new variable is created. For example, in a nonmagnetic material the order parameter is the magnetization M, which in the absence of a magnetic field is zero by time-reversal symmetry. The state in that case is specified by the usual intensive variables P and T.
It is possible to predict that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = -T \ln{<e^{-\beta H}>}} in the new system is a different mathematical function than in the old. For instance, call the new variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Then in general we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = F(V,T,\psi)}
We calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = F(V,T)}
by appending to this the equilibrium condition
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac{\partial F}{\partial \psi} = f = 0 }
where f is the generalized force variable (like the magnetic field H) corresponding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi} . Above the critical temperature Tc, this is satisfied by symmetry; below, it is nontrivial. Then from the las two equations the result is a new function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F'(V,T) } , which is not analytic at Tc. This is Landau's essential insight.
In simplest terms, it is quite clear that the First Theorem requires that F have a boundary of singularities between the two regimes of symmetry, and that therefore analytic continuation between the two is not possible.
Generalized "rigidity"
When we move one end of a ruler, the other moves the same distance, such action at a distance is not built into the laws of nature except in the case of the long-range forces such as gravity or electrostatics. It is strictly a consequence of the fact that the energy is minimized when symmetry is broken in the same way throughout the sample: the phase and angle variables want to be uniform, so that the orientation and position of the lattice is the same everywhere. Of course, in general they are not quite the same, since the lattice can deform elastically, but nonetheless the lattice transmits that force from one end to the other even in equilibrium and without having to flow constantly like a viscous liquid. To break down the rigidity completely, we must supply the condensation energy of a macroscopic piece of the sample, which is very large.
The generalization of this concept to all of the instances of broken symmetry is it call here generalized rigidity. For instance, permanent magnets are so because the magnetization cannot change a little at a time. Superconductivity is the phase rigidity of the electron pair fluid.
In general, there is a rigidity or elastic constant associated with every phase transition to a state with broken continuous symmetry, which prevents the new state from being destroyed by thermal fluctuations. For example, a liquid has no associated rigidity; a nematic phase has an associated rotational elastic constant; a smectic phase has an associated layer modulus; a crystal has an associated shear modulus; a heisenberg magnet has an associated spin-wave stiffness; a superfluid has an associated superfluid density. There are all properties which act to preserve a broken symmetry.
Defect structures
There is a general rule that the breakdown of the generalized rigidity property, along with the resulting dissipation, is a consequence of the formation and motion of defect structures which are usually macroscopic in size.
The twin models for such effects are the domain theory of ferromagnetism, due to Landau (1941), Block (1930) and others, and the dislocation theory of G. I. Taylor (1934), Burgers (1939, 1940), and others. These two cases demonstrate nicely the one general statement which will be justified by the topological theory: that a one-dimensional order parameter allows only two-dimensional ("wall") defects; and that a two-dimensional order parameter allows linear defects such as dislocations, but not necessarily always; while a three- or more- dimensional case may allow point defects.
Clearly in any broken-symmetry system we can imagine forces which would disorient the order parameter in one region relative to another. As a simple example could be that different parts of the sample may have grown with different order parameters and eventually meet in the middle. In what ways can the system respond?
The most obvious and simplest is a boundary or "domain wall" (see right figure): one simply has two or more regions. each locally homogeneous, separated by boundaries. In the case of the one-dimensional order parameter, there is only a discrete set of local equilibrium states (directions of M for a ferromagnet, for instance, or of P for ferroelectric), and there must be a two-dimensional boundary (for a 3D sample) shape of the boundary or other singularity is determined by competition between the forces of generalized rigidity. In the boundary case, characteristically the wall is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx}
one lattice constant thick-- essentially, there is no length parameter except the fundamental microscopic length. Thin boundaries cannot move continuously in space --they are located at a specific crystal plan and must overcome an activation energy to move to the next.
In general, the response to external forces tending to twist or reverse the magnetization must in the first instance come from the motion of these boundaries. To make a permanent magnet, one can proceed in two ways: either to pin the existing boundaries, i.e., to make a very impure material, or to remove them, i.e., to make i of very small particles. Thus the response properties of magnets are wholly conditioned by the defect structures. This is, in fact, the general case.
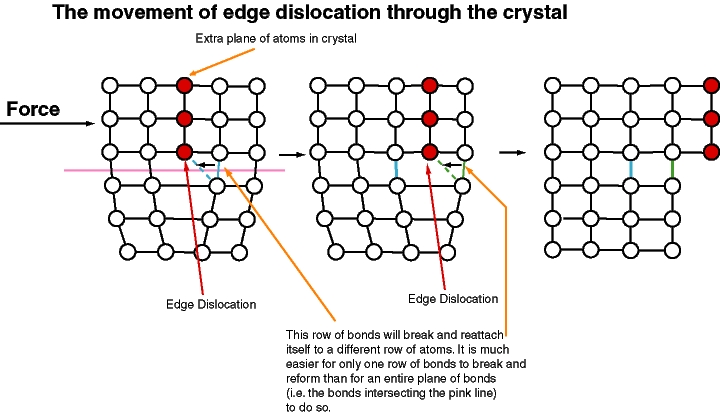
A second type of defect is a line defect. An example is the dislocation (see next figure). We can imagine following a closed path through a crystal along which the local phase varies gradually, corresponding to a small local strain, but then returns to the original phase changed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle 2\pi}
. There must be associated a line of singularity where the lattice structure is essentially destroyed.
The two basic types of dislocations are edge dislocations, where an extra plane of atoms has been interpolated ending at a line singularity; and screw dislocations, where the lattice has the topology of a screw.
The easiest way in which a crystal can continuously slide against itself is by the continuous flow of dislocations across a line between the two. Again, there are two ways to make a strong crystal: the easy way is to pin the dislocations, one version of which is called work hardening; the hard way is to eliminate them altogether as in a "whisker" crystal.
Goldstone's Theorem
In this section, we demonstrate what is known as the Goldstone's Theorem, which shows how the emergence of long-range correlations arises as a generic feature of broken continuous symmetry.We concentrate on the form of the spin-spin correlation function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \alpha }(\mathbf{x})=<\phi _{\alpha }(\mathbf{x})\phi _{\alpha }(\mathbf{0})>-<\phi _{\alpha }(\mathbf{x})><\phi _{\alpha }(\mathbf{0})>} Technically, it can be evaluated by taking functional derivatives of the functional :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[j]=ln Z[j]}
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \alpha }(\mathbf{x-y})=\frac{\delta ^{2}}{\delta j_{\alpha }(\mathbf{x})\delta j_{\alpha }(\mathbf{y})}F[j]}
We note that for an isotropic system, correlations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \beta }(\mathbf{x})} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \neq \beta } vanish by symmetry. Consider a system with continuous symmetry (n>1), in the ordered phase, and imagine applying a small external field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{a}(\mathbf{x})} . Since the system is assumed to be isotropic, the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z[j]} , which is a scalar quantity, must be independent of the direction of the order parameter.It will, therefore remain unchanged if we perform an infinitesimal rotation of the field direction by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \theta } in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\beta ,\gamma )} plane.Only the components Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\beta }(\mathbf{x})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }(\mathbf{x})} are affected.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\beta }^{'}(\mathbf{x})=j_{\beta }(\mathbf{x})-\delta \theta j_{\gamma }(\mathbf{x})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }^{'}(\mathbf{x})=j_{\gamma }(\mathbf{x})-\delta \theta j_{\beta }(\mathbf{x})}
The variation of F[j] leads to:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=\int d\mathbf{x}[\frac{\delta F}{\delta j_{\beta }(\mathbf{x})}j_{\gamma }(\mathbf{x})-\frac{\delta F}{\delta j_{\gamma }(\mathbf{x})}j_{\beta }(\mathbf{x})]}
Taking another variation with respect to gives
Now, let us assume that the initial field was a function in the direction, i.e. . In this case, and we conclude that,
or in the momentum space:
Since, we are in the ordered phase, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \rightarrow const.} when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j\rightarrow 0,} and we conclude
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})=\infty !}
As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})} is an even function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}} (by inversion symmetry), the most natural possibility is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q}=0)\sim 1/q^{2}}
We note that the direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma } can be chosen to be any of the transversal directions to the ordering vector direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } .The corresponding correlation function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})=G_{\perp }(\mathbf{q=0})} thus described the transverse correlations, which we find to be long-ranged:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\perp }(\mathbf{x})\sim \frac{1}{\left | \mathbf{x} \right |^{d-2}}}
This arguement is completely general. It applies to any model with broken continuous symmetry, classical or quantum, and is also valid at any temperature throughout the ordered phase.The excitations associated to these transverse fluctuations are called Goldstone modes or in quantum systems as Goldstone bosons.
Collective excitations
The Hamiltonian describing the internal interactions in a macroscopic system still obeys the initial transformations of the symmetry group. The state, however, does not. Immediate consequences of this are
A) Elementary collective excitations of the system, whose character can be determined largely from information about the details of the Hamiltonian and the broken symmetry.
B) There exist new static properties in the broken-symmetry phase that we can call generalized "rigidity". (Described in detail above)
C) Order parameter defects. (Described in detail above)
There are two cases of consequence A:
Case 1) The new broken symmetry state is an eigenstate of the Hamiltonian. (The order parameter is a constant of the motion).
e.g. : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle < \vec{S_{tot}} > \neq 0 } in ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S_{tot}} = \sum_{i=1}^{N}\vec{S_i} }
Case 2) The new broken symmetry state is not an eigenstate of the Hamiltonian. (The order parameter is not a constant of the motion).
e.g. A crystal cannot be an eigenstate of the Hamiltonian. Positions are fixed, and thus will not commute with the kinetic energy operator.
In Case 1) Spin waves disperse quadratically with momentum, In Case 2) Spin waves disperse linearly with momentum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega \propto k }
There tend to be more examples of case 2, such as crystals, antiferromagnets, nematics (liquid crystals), etc.
Phonons
At low enough temperatures, a system of particles occupies a ground state that does not display the full symmetries of the Hamiltonian. Important and interesting properties of matter appear as elementary excitations and fluctuations of this symmetry breaking ground state.
The low energy excitations of of the crystaline ground state are vibrational modes or phonons. A phonon is a description of a special type of vibrational motion, in which a lattice uniformly oscillates at the same frequency i.e. normal modes. Thereby, phonon is a quantum notion of normal modes. These normal modes are important because any arbitrary lattice vibration can be considered as a superposition of these elementary vibrations.
The name phonon comes from the Greek word φωνή (phonē), which translates as sound, because long-wavelength phonons give rise to sound.
To learn more about these vibrational excitations, consider the following Hamiltonian whose ground state is a cubic crystal:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{j=1}^N {p_j^2 \over 2m} + \sum_{i>j}V (\mathbf{r_i} -\mathbf{r_j})\ } .
We will make two assumptions:
1. The mean equilibrium position of each ion is a Bravais lattice site ([http://en.wikipedia.org/wiki/Bravais_lattice). With each ion we associate a particular Bravais lattice site R, about which the ion oscillates.
2. The typical displacement of each ion from its equilibrium position are small compared with the interionic spacing.
Assumption 1 makes sure a Bravais lattice exists in spite of ionic motion. The lattice describes the average ionic configuration rather than the instantaneous one. One thing to be remembered, although this assumption permits a wide range of possible ionic motion, is that it does not allow for ionic diffusion: The oscillation of each ion are assumed to be forever about a particular lattice.
Assumption 2 will give rise the harmonic approximation: the expansion in the displacement up to second order only. The results obtain in the harmonic approximation are often in agreement with observed properties of solid. But, some properties still can not be explained by harmonic theory, and one has to go to anharmonic theory (higher order in the expansion in displacements) to account for those properties.
Using assumption 1, we denote the position of the ion whose mean position is R by r(R). In reality, r(R) will deviate from its average value R, and at any given time we can write:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}(\mathbf{R})=\mathbf{R}+\mathbf{u}(\mathbf{R})} ,
where u(R) is the deviation from equilibrium of the ion whose equilibrium site is R. In a cubic lattice
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}=a(l\hat{x}+m\hat{y}+n\hat{z})} ,
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a} is lattice constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle l,m,n} are integers.
A pair of atoms separated by r contributes an amount of potential energy U(r). We can write
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}{2}\sum_{RR'}V(\mathbf{r(R)-r(R')})=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .
to make the dependence of the potential energy on the dynamical variables u(R) explicit.
For kinetic energy term, we rewrite
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{p}_{j}\rightarrow \mathbf{p(R)} } .
The Hamiltonian then reads:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{R}{p(\mathbf{R})^{2} \over 2M}+\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .
Assumption 2 now allows us to make the harmonic approximation, based on the expectation that the atoms will not deviate substantially from their equilibrium positions. First we expand the potential energy V about its equilibrium position using Taylor's expansion,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf{r+a})=f(\mathbf{r})+\mathbf{a}\cdot\nabla f(\mathbf {r})+\frac{1}{2!}(\mathbf{a}\cdot\nabla)^{2}f(\mathbf{r})+\frac{1}{3!}(\mathbf{a}\cdot\nabla)^{3}f(\mathbf{r})+...} .
Applying this expansion to each term in the potential energy, with r = R - R' and a = u(R) - u(R'), we get
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})=&\underbrace{\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})}_{U^{eq}}+\underbrace{\frac{1}{2}\sum_{RR'}(\mathbf{u(R)-u(R')}) \cdot\nabla V(\mathbf{R-R'})}_{=0}\\ &+\underbrace{\frac{1}{4}\sum_{RR'}[(\mathbf{u(R)-u(R')})\cdot\nabla]^{2}V(\mathbf{R-R'})}_{U^{harm}}+\underbrace{\text{terms in higher order in } \mathbf{u(R)}}_{U^{anharm}}\\ \end{align}}
The coefficient of u(R) in the linear term above is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{R'}\nabla V(\mathbf{R-R'})} .
This is just minus the force exerted on the atom at R by all other atoms, when each is placed at its equilibrium position. Therefore, it must vanish because there is no net force on atoms in equilibrium.
The harmonic approximation consists in dropping all terms beyond second order in u(R), or else neglecting the terms in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{anharm} } .
Within this approximation, we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U=U^{eq}+U^{harm}} ,
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{eq}=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}=\frac{1}{4}\sum_{\mathbf{RR'}}[\mathbf{u_{\mu}(R)-u_{\mu}(R')}]\phi_{\mu \nu}[\mathbf{u_{\nu}(R)-u_{\nu}(R')}]} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\mu \nu}(\mathbf{r})={\partial^{2}V(\mathbf{r})\over \partial r_{\mu}\partial r_{\nu}}}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U^{eq}} is just a constant (i.e., independent of the u's and P's), it can be ignored in many dynamical problems, and one frequently acts as if the total potential energy were just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U^{harm}} , dropping the superscript altogether when no ambiguity is likely to result.
The harmonic approximation is the starting point for all theories of lattice dynamics. Anharmonic corrections to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U} , especially those of third and fourth order in the u's, are of considerable importance in understanding many physical phenomena. They are generally treated as small perturbations on the dominant harmonic term.
The harmonic potential energy is usually written in the more general form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}=\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}
with
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{\mu \nu}(\mathbf{R-R'})=\delta_{\mathbf{R,R'}}\sum_{\mathbf{R''}}\phi_{\mu \nu}(\mathbf{R-R''})-\phi_{\mu \nu}(\mathbf{R-R'})} .
Then, the harmonic Hamiltonian becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{harm}=\sum_{\mathbf{R}}\frac{1}{2M}p(\mathbf{R})^{2}+\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}
We will extract the eigenvalues from this Hamiltonian. Later, we will find that the energy due to lattice vibration of an N-ion harmonic crystal can be be obtained as the sum over 3N discrete normal modes. These discrete normal modes or quasi-particles are called phonons.
We proceed as follows: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} be the frequency and polarization vector for the classical normal mode with polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle s} and wave vector k. Now define the "phonon annihilation operator":
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k\cdot R}}\mathbf{\epsilon}_{s}(\mathbf{k})\cdot \left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}+i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{p(R)}\right]} ,
and its adjoint, the "phonon creation operator":
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k\cdot R}}\mathbf{\epsilon}_{s}(\mathbf{k})\cdot\left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}-i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{p(R)}\right]} .
The canonical commutation relations,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),p_\nu (\mathbf{R'})]=i\hbar\delta_{\mu\nu}\delta_\mathbf{R,R'}} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),u_\nu (\mathbf{R'})]=[p_\mu (\mathbf{R}),p_\nu (\mathbf{R'})]=0} ,
the identity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{R}e^{i\mathbf{k\cdot R}}=\begin{cases}0,\quad\quad\quad&\mathbf{k}\quad \text{is not a reciprocal lattice vector},\\ N,&\mathbf{k}\quad \text{is a reciprocal lattice vector},\end{cases}}
and the orthonormality of polarization vectors
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon_s(k)\cdot\epsilon_{s'}(k)}=\delta_{ss'}, \quad \quad s,s'=1,2,3}
yield the commutation relations
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&[a_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=\delta_\mathbf{kk'}\delta_{ss'},\\ &[a_{\mathbf{k}s},a_{\mathbf{k'}s'}]=[a^\dagger_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=0.\end{align}}
Now one can express the coordinates and momenta in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&\mathbf{u(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar \over 2M\omega_s(\mathbf{k})}(a_{\mathbf{k}s}+a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k\cdot R}},\\ &\mathbf{p(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar M\omega_s(\mathbf{k})\over 2}(a_{\mathbf{k}s}-a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k\cdot R}}.\end{align}}
Equation above can be obtained by substitution of equations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}}
, and by use of the "completeness relation" that holds for any complete set of real orthogonal vectors,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{s=1}^3[\mathbf{\epsilon}_s(\mathbf{k})]_\mu[\mathbf{\epsilon}_s(\mathbf{k})]_\nu=\delta_{\mu\nu},}
together with identity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{k}e^{i\mathbf{k.R}}=0,\quad\quad \mathbf{R}\neq 0.}
Having expressed u(R) and p(R) in terms of annihilation and creation operators, we can also write the harmonic Hamiltonian in terms of the new operators. It can be shown that the kinetic energy is given by:
Next, we define the dynamical matrix D(k)
Now let the polarization vectors be the eigenvectors of the dynamical matrix ,
Using these facts, we can write the potential energy as
Adding the kinetic and potential terms together, we get that
and, using the commutation relations, we find that
This is nothing more than the sum of 3N independent oscillators, one for each wave vector and polarization. When a Hamiltonian is divided into a sum of commuting sub-Hamiltonians, its eigenstates are simply all products of the eigenstates of sub-Hamiltonians, and the eigenvalues are the sum of the individual eigenvalues of the sub-Hamiltonians. We can therefore specify an eigenstate of H by giving a set of 3N quantum numbers , one for each of the 3N independent oscillator Hamiltonians . The energy of such a state is
In the corpuscular description the independent oscillators that give rise to normal modes can be regarded as quasiparticles, i.e. phonons.
Below we give an example of normal modes (phonons) of a monoatomic 3D bravais lattice with short ranged interactions. The main purpose in this case is to seek the dispersion relation .
We begin with 3N equations of motion (since we have N ions in 3D):
or in matrix notation,
We are looking for solutions in the form of simple plane waves:
where is the polarization vector of the normal mode mentioned above.
We continue to use the periodic boundary condition which is
for each of the three primitive vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a_i}
, where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N_i}
are large integers satisfying
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N=N_1N_2N_3. }
This restricts the allowed wave vectors k to
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}={n_1\over N_1}\mathbf{b_1}+{n_2\over N_2}\mathbf{b_2}+{n_3\over N_3}\mathbf{b_3} }
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i}
integral and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{b_i}}
are the reciprocal lattice vectors satisfying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{b_i\cdot a_j}=2\pi \delta_{ij}}
. Generally, it is convenient to take crystal cell to be in the first Brillouin zone.
With the assumption that the solutions are in the simple planewave vectors form, the equation of motions become eigenvalue problems, i.e.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2\mathbf{\epsilon}=\mathbf{D(k)\epsilon} }
D(k) is the dynamical matrix defined above. The three solutions to equation above for each of the N allowed value of k, give 3N normal modes. We manipulate D(k), using the property that the interaction is short ranged and only nearest neighbour contributions survive:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{D(k)}&={1 \over 2}\sum_\mathbf{R}\mathbf{D(R)}[e^{-i\mathbf{k\cdot R}}+e^{i\mathbf{k\cdot R}}-2]\\ &=\sum_\mathbf{R}\mathbf{D(R)}[cos(\mathbf{k\cdot R})-1]\\ &=-2\sum_\mathbf{R}\mathbf{D(R)}sin^2 ({1\over 2}\mathbf{k\cdot R}).\\ \end{align}}
Equation above explicitly demonstrate that D(k) is an even function of k and a real matrix. It can be further shown that D(k) is a symmetric matrix. One theorem in matrix algebra states that every real symmetric 3D matrix has three real eigenvectors, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon_1, \epsilon_2, \epsilon_3}}
which satisfy
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)\epsilon_s (k)}=\lambda_s \mathbf{(k)\epsilon_s(k)} }
Evidently the three normal modes with wave vector k will have polarization vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})}
and frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s\mathbf{(k)}}
given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})=\sqrt{{\lambda_s\mathbf{(k)}\over M}} }
To determine the k dependence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s}
at small k, we have to remember when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k\cdot R}}
is small for all R connecting sites whose ions have any appreciable interaction, then we can approximate the sine in dynamical matrix equation by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin^2 ({1\over 2}\mathbf{k\cdot R})\approx ({1\over 2}\mathbf{k\cdot R})^2, }
therefore
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}\approx -{k^2 \over 2}\sum_R\mathbf{(\hat{k}\cdot R)^2 D(R)}. }
Consequently, in the long-wavelength or small k limit, we can write
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})=c_s(\mathbf{\hat{k}})k, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_s(\mathbf{\hat{k}})}
are the squqre roots of the eigenvalues of the matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -{1 \over 2}\sum_R\mathbf{(\hat{k}\cdot R)^2 D(R)}. }
So, the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})}
is linear in the long-wavelength limit. This is a result of the approximation of short-ranged interaction! For long-ranged interaction, such as the Coulomb inteaction, the dispersion relation would differ. However, it is guaranteed that so-called "soft modes", with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(\mathbf{k}) \to 0 }
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k| \to 0 }
, exist. These modes are the Goldstone-modes corresponding to the broken translational symmetries.
In 3D, it is important to consider not only the behavior of the frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})} but also the relation between the direction of polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} and the direction of propagation k. In an isotropic medium, we can always choose the three solutions for a given k so that one branch (the longitudinal branch) is polarized along the direction of propagation and the other two transverse branches are polarized perpendicular to the direction of propagation. In an anisotropic crystal the polarization vectors need not be simply related to the direction of propagation unless k i invariant under certain symmetry of the crystal.
Spin Waves and the Heisenberg Ferromagnet
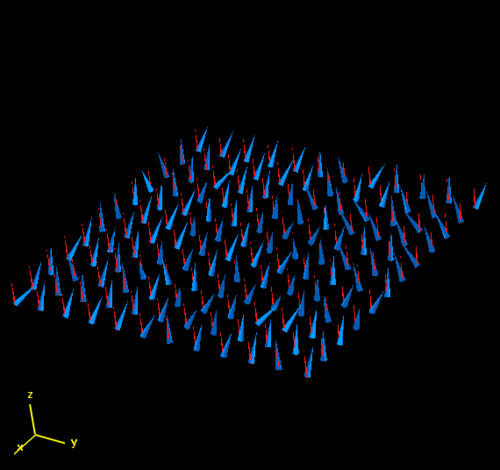
Spin waves (also called magnons) are the classical normal modes or collective quantum excitations of a magnetically ordered system. The projection of spin on an atom is reduced by one, but the excitation is not localized and propagates in the form of a wave throughout the lattice. In the long-wavelength limit, spin waves are the hydrodynamic modes related to the broken symmetry resulting from alignment (or anti-alignment) of the spins. For an antiferromagnet, spin waves have the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \propto q } and for a ferromagnet, spin waves have the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \propto q^2 } .
Spin waves can be derived by constructing a low lying excited state to an ordered ferromagnet. Assuming a cubic lattice, we can write the Hamiltonian for the isotropic (Heisenberg) ferromagnet as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle J(R - R') } is short ranged, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle J > 0 } . The ground state occurs when all of the spins are aligned. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S\rangle } is the maximum spin projection, then the ground state is : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0 \rangle = \prod_R |S\rangle_R}
Trying to lower a single spin to create an excited state eigenstate does NOT produce an eigenstate. For example, we can create a state which is the same as the ground state, except the spin at R has been lowered:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle = \frac{1}{\sqrt{2S}}S^{-}(R)|0\rangle }
However, the Hamiltonian will flip the spin at R back up, and then flip another spin at R' down. First we rewrite the Hamiltonian, using the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{\pm}(R) = S^x(R)\pm iS^y(R)} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^x(R) \vec S^x(R') -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^y(R) \vec S^y(R') }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R) }
Now examine how this Hamiltonian acts on our proposed state:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|R_0\rangle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R')|R_0\rangle - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R)|R_0\rangle }
The first term (ignoring constants):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec S^z(R) \vec S^z(R')|R_0\rangle = \vec S^z(R) \vec S^z(R')\vec S^-(R_0)|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R)\left( \left[S^{z}(R'),S^{-}(R_0) \right] + \vec S^{-}(R_0)\vec S^z(R') \right) |0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R) \left( -S^{-}(R_0)\delta_{R',R_0} + S S^{-}(R_0) \right) |0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \delta_{R,R_0}\delta_{R',R_0}S^{-}(R_0)|0\rangle - S\delta_{R',R_0}S^{-}(R_0)|0\rangle - S\delta_{R,R_0}S^{-}(R_0) + S^2S^{-}(R_0)|0\rangle }
Now returning the constants: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R')|R_0\rangle = \frac{S}{2}\sum_{R\neq R'} J(R - R_0)|R_0\rangle + \frac{S}{2}\frac{S}{2}\sum_{R\neq R'} J(R_0 - R')|R_0\rangle - \frac{S^2}{2}\sum_{R\neq R'} J(R - R')|R_0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S\sum_{R\neq R'} J(R - R')|R_0\rangle + E_0 }
Where the last term, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle E_0 } , is the ground state energy. So far Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } appears to be an eigenstate of the Hamiltonian. However, we much still examine the second term:
The second term: (ignoring constants)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-}(R')S^{+}(R)|R_0\rangle = S^{-}(R')S^{+}(R)S^{-}(R_0)|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S^{-}(R')\left[S^+(R),S^-(R_0) \right]|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S^-(R')\left(2S^z(R)\delta_{R,R_0} \right)|0\rangle = 2S\delta_{R,R_0}S^{-}(R')|0\rangle }
Now returning the constants:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-S\sum_{R\neq R_0} J(R_0 - R)|R\rangle }
Therefore, we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|R_0\rangle = E_0|R_0\rangle + S\sum_{R\neq R_0} J(R_0 - R)\left(|R_0\rangle - |R\rangle\right) }
Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle} is not an eigenstate of the Hamiltonian. Although Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } is not an eigenstate, it is a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } and other states with one lowered spin.
So we must continue to seek and excited state eigenstate. Because J depends on R and R' only in a translationally variant combination, we can seek eigenstates of the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec k \rangle = \frac{1}{\sqrt{N}}\sum_R e^{i \vec k \cdot \vec R }|R_0\rangle }
This makes a superposition of phase factors of states where only one spin is flipped. Applying the Hamiltonian to this state yields:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|\vec k \rangle = E_0|\vec k \rangle + \frac{S}{\sqrt{N}}\sum_{R\neq R'} J(R - R') \left( e^{i\vec k \cdot \vec R }|R'\rangle - e^{i\vec k \cdot \vec R'}|R\rangle\right) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\sum_{R} J(R - R')|\vec k \rangle - \frac{S}{\sqrt{N}}\sum_{R}\left( \sum_{R'}e^{i\vec k \cdot (\vec R' - \vec R) } J(R - R')|R\rangle \right) e^{i\vec k \cdot \vec R} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\sum_{R} J(R - R')\left(1 - e^{i\vec k \cdot (\vec R - \vec R') } \right)|\vec k \rangle } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\left(\sum_{R} J(R)(1 - e^{i\vec k \cdot (\vec R) } )\right)|\vec k \rangle }
since we can write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{R} J(R)\left(1 - e^{i\vec k \cdot \vec R } \right) = 2\sum_{R} J(R) \sin^2\left(\frac{\vec k \cdot \vec R}{2}\right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec k) = E_0 + 2S\sum_{R} J(R) \sin^2\left(\frac{k \cdot R}{2}\right) }
For small k, this has dependence on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle k^2 }
. And so we have the k dependence of the energy dispersion for one spin-wave mode at wave vector k for an isotropic ferromagnet. For additional spin waves an interaction term must be included due to the scattering of spin waves off one-another.
Spin Waves and Magnetization
The energy dispersion of the spin waves can be used to find the low-T behavior of the magnetization M(T). To do this, the ferromagnetic spin waves are treated as a non-interacting gas of bosons. Since a spin wave is a delocalized flip of a spin, each spin wave lowers the magnetization by one unit.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(T) = NS - \sum \frac{1}{\exp(\beta \epsilon) - 1} }
where the second term is the total number is spin waves at temperature T, with (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{1}{k_B T} } ).
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(T) = M(0)\left( 1 - \frac{V}{NS}\int \frac{d^3k}{(2\pi)^3} \frac{1}{\exp(\beta \tilde{\epsilon}) - 1}\right) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle M(0) = NS} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tilde{\epsilon} = 2S\sum_{R}J(\vec R) \sin^2 \left(\frac{\vec k \cdot \vec R}{2}\right) } . Since we're looking for low - T asymptotics we expand this, using the approximation that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\tilde{\epsilon} = Vk^2 } where V is some constant.
Spin Wave (SW) Theory
The spin-wave theory, due originally to Anderson, which is widely used to obtain results for many different systems, gives results for the energies of the elementary excitations or spin waves. The method works for both ferromagnets and antiferromagnets, it works in 2D and 3D as well as 1D, and it works for arbitrary spin – not just for spin-1/2. The ferromagnetic version is rather simple and the results are usually exact. The antiferromagnetic version is more complicated and the results are approximate. However,these results are still in reasonable correspondence with exact results.The basic idea of spin-wave theory is to replace the spin operators by bosons. As we have seen, spin operators behave like fermions on a given site, but like bosons where different sites are concerned.
For a general spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} and a single site the corresponding basis is again the eigenstates of written as where the values of m are
and the states are orthogonal and normalized (i.e. orthonormal). Let be the number of deviations from ,the state of maximum .
Recall the following relations:
We now introduce boson operators for a single site which reproduce most of the above properties. There are various ways of doing this but we shall only consider the most useful and widely used, called the Holstein-Primakoff transformation.
Let be boson creation and destruction operators, with the usual commutation relations
etc.
We now interpret the number of bosons as the number of deviations from the state . State has deviations and the number operator for bosons is so
We can represent as
, since
And
Proof:
Similarly for
Note that the Holstein-Primakoff transformation is exactas far as the states are concerned. However, in principle it is possible to have more than S bosons, i.e. a state of the form
where
These states are unphysical and they can never be reached if we use the exact transformation.However, we shall now approximate the transformation and this allows coupling to the unphysical states. The approximation will only be valid provided the admixture of the unphysical states is ‘small’ in some sense. Mathematically it is very difficult to handle a transformation involving square roots. The approximation we shall use is based on the assumption that the states of interest all have small probabilities of having deviations on any particular site and a negligible probability of having two or more deviations on the same site. This is equivalent to saying
1. The total number of deviations , i.e.,
2. Bound states in which deviations cluster together cannot be treated accurately.
Under these approximations, we can write
for simple W theory, and
For simple SW theory we now obtain a very simple result
Ferromagnetic Spin-Wave Theory
Consider the Heisenberg model with nearest neighbour ferromagnetic coupling
where
, j runs over all sites, and runs over all numbers. The ground state is a state with all atoms aligned. Usually we take this to be the state in which all atoms are in the state. Other degenerate ground states can be easily constructed from this state by using the lowering operator for the whole system . Writing
Using the simple SW results,
The last term here involves four boson operators. For consistency with our previous approximation we must neglect this term. The first term is the energy of the ground state (all N spins up). Calling the first term as , and using our approximation, we get
We go to Fourier space to diagonalize this Hamiltonian. Define
The reverse transformations are
with
Using this,
where
. These are the energies relative to the fully alligned ground state of the ferromagnetic spin waves.
A solved problem for spin waves
Hydrodynamics
In principle, many-body systems can be studied microscopically by writing down all the equations of motion but that is practically impossible due to the large number of degree of freedom. Thermodynamics is by far a more practical way to study many-body systems. In this theory, many-body system in equilibrium states can be described macroscopically by a small number of thermodynamic variables (or macroscopic degree of freedom), such as internal energy, temperature, pressure, magnetization, etc. In a system with broken continuous symmetry, the theory can be extended to describe the spatially non-uniform states in which the elastic distortion (small amplitude distortion) from the homogenous states is of long wavelength and slowly varying (low frequency). Because of the long wavelength of the elastic distortion, the departure from homogenous states is small. In this chapter, we will derive the equations governing the dynamics of the system undergoing such kind of distortions based mostly on what we have learned in thermodynamics.
Conserved and broken-symmetry variables
Thermodynamic equilibrium is created and maintained by the collisions between particles. These collisions are characterized by the time interval between two successive collisions experienced by one particle or by its mean free path which is equal to velocity times . Now, consider a distortion that oscillates in time and space with frequency and wave number . If the disturbance has long wavelength and low frequency, i.e. and , there will be enough time and space for the collisions to locally equilibrate the system. That is why we can really use thermodynamics to study the system in this situation. Most disturbances in many-body systems have characteristic frequencies that are of the order of and they decay quickly to equilibrium. There are, however, certain variables that are guaranteed to have slow temporal variations at long wavelength. There are 2 such categories:
- densities of conserved variables, and
- broken symmetry variables
The density of conserved variable such as number density follows the conservation law:
When Fourier transformed, such equation implies that when the frequency goes to zero so does that wave number, because the time derivative brings down a factor of in the first term whereas the gradient yields a factor of in front of the second term. Therefore the disturbances in the densities of conserved variables are guaranteed to have long wavelength and low frequency.
For a system with broken continuous symmetry, spatially uniform changes in elastic variables lead to new equilibrium states that are stationary in time. For example, if we apply a uniform translation on a crystal, it will end up being in the same state as before. Therefore, frequency associated with a displacement of continuous broken symmetry elastic variable is also zero. Spatially non-uniform displacement, however, will have non-zero characteristic frequency. Therefore the disturbance in the densities of broken symmetry variables are also guaranteed to have long wavelength and low frequency.
Historically, the dynamics of variables with long wavelength and low frequency was first studied extensively in water. The dynamics of water in motion is called hydrodynamics. Nowadays, the term hydrodynamics is not just limited to water, it is used for long-wavelength and low-frequency dynamics of conserved and broken-symmetry variables in any systems, such as spin systems and liquid crystals, etc.
Planar Ferromagnet
The procedure for deriving hydrodynamic equations is as follows. First, because hydrodynamics is basically a perturbation (small amplitude disturbance of long wavelength and low frequency) from thermodynamic equilibrium, we have to generalize the thermodynamic treatment to include all the conserved and broken-symmetry variables. In the other words, we have to write down the first law of thermodynamics with taking into account those variables. Secondly, we have to identify the reactive or nondissipative couplings, which couples the time derivative of a hydrodynamic variable of one sign to another variable of the opposite sign under the time reversal. Next, we have to derive the irreversible dissipative couplings. Both reactive and dissipative couplings, which relate currents to thermodynamic fields, are called constitutive relations. All that together with conservation law, thermodynamic relations allow us to find out the hydrodynamic equations of the system. That procedure will be illustrated in the planar ferromagnetic system.
A planar ferromagnet is described by the Hamiltonian.
The hydrodynamic variables of this system at high temperatures (disordered phase) are energy , the total spin , both of which are conserved quantities. Let's start with the discussion on the disordered phase.
Disordered Phase
The fundamental thermodynamic relation is
The equation gives
- for small
next, we have to introduce the conservation law which is given by the continuity relation for both energy and magnetization along the direction
From the fundamental thermodynamic relation and the conservation law, we get which gives,
Next, consider (just mathematical identities)
which we substitute back into the equation above, so that
which gives
Now, we perform an integration over all volume, and using the Gauss' Theorem keeping in mind that the current vanishes at the surface we get :
with ,
At this point, we have to consider whether or not dissipation exist in the system. If it does not exist, then there is no entropy production, hence the term vanishes as a result and vanish accordingly. Which make sense because in the system without dissipation, there should be no change in the energy nor magnetization so there is no current for both of them. So :
In the case of dissipation, what we have to consider is how the entropy changes. Our equation above allows the entropy production to be positive or negative, mathematically. Therefore, we impose a constraint that the rate of change for the entropy to be strictly positive in our constitutive relations. We see, that this can be done by setting the integrand to be positive.
Let, and where is the thermal conductivity and is just a transport coefficient (or actually we can just say that both are just transport coefficients).
We now see that the rate of change of the entropy becomes
In addition, dissipative currents of one sign under time reversal operation must be proportional to the variables of the opposite sign.
With the constitutive relations above, we rewrite the continuity relations as follows:
Going further, these relations can be closed by using thermodynamic relations
,
which gives us two diffusion equations :
where is the thermal diffusion coefficient and is the magnetization diffusion coefficient.
Each of these diffusion equations corresponds to one mode. And we see that there is always one mode associated with each conserved variable.
Ordered Phase
The ordered phase of the planar ferromagnet is characterized by an order parameter and to describe it, we need an additional slow/hydrodynamical variable . This additional slow variable modifies the fundamental thermodynamic relation as follows
Therefore, we get
And as before, we address the conservation law in the form of the continuity equation for all conserved variables
We then take the time derivative of the entropy density :
And again using the mathematical identities :
and substitute them into the equation for the rate of change of the entropy density:
Grouping terms with the same factor and integrating gives :
In the absence of dissipation which results in
The result from the non-dissipative process above implies
Therefore taking time derivative of ,
or, more explicitly :
Removing all spatial derivative operator from the l.h.s and r.h.s, we get:
Which is a wave equation whose frequency is
So, we have a new mode which exists in the ordered phase (below a certain critical temperature ) which is a SPIN WAVE.
Now, let's consider the situation with dissipation.
Constitutive relations can be written as
(here we have direction dependence since we are working with ordered phase of planar ferromagnet)
(here we are working with a scalar quantity, no direction dependence)
Linearing about and or and on average, respectively
Combining with the following thermodynamic relation
we obtain the equation of motion for the energy which is a diffusive mode
Now let's solve for the equation for the spin wave excitation from the system of equations that coupled the fluctuations of and . We have
It follows that
One way to solve this coupled system is to go to Fourer space
and similarly for
We derive to the following system of equations in Fourier space
This system can be decoupled by diagonalizing the 2 by 2 matrix. Let be the eigenvalue of the matrix, we have
This quadratic equation can be solved easily, yielding
At small we have
So in the present of dissipation we obtain a damping spin wave. The osillating frequency is characteried by the real part of which is linear in . Whereas, there damping frequency is characterized by the imaginary part of which is proporotioanl to .
In conclusion, at high temperature, there are two diffusive modes associated with two conserved quantities (energy and component of the total magnetization). At low temperature, the system is characterized by energy , and broken symmetry variable . In this case, the equation of motion for the energy is uncoupled and is still diffusive. On the other hand, and are coupled to each other, resulting in two damping wave modes for and .
Summary
In the previous section, we have just studied the hydrodynamics of a simple model of planar ferromagnet. Many concepts and results are quite general for the hydrodynamics of all systems. The most important of these are listed below:
- Long wavelengh, low frequency excitations are related to conservation laws and broken symmetry.
- There is exactly one mode associated with each conservation law and each broken symmetry.
- Currents of hydrodynamic variables contain reactive and dissipative parts.
- In the absence of reactive couplings, the hydrodynamic modes are diffusive.
- Diffusion constants are the ratio of a transport coefficient to a susceptibility.
- The velocity of propagating modes are square roots of the ratio of a reactive transport
- and a susceptibility.
- Dissipative coefficients are related to current correlation function via Kubo Formula.
- Elementary excitations from the ground state can be described by a harmonic Hamiltonian.
- There must be a zero-frequency, zero wave number mode in systems with a continuous broke symmetry.
Adiabatic principle
When entering research people usually find that the most difficult question is where to start, especially when confronted with something that is actually new.
The adiabatic continuity principle tells us to search for the right simple problem when confronted with a complicated one. As long as the simple problem describes a correct physical state of matter, and so we do not risk crossing a phase boundary, we can start with some non-interacting model system as an unperturbed Hamiltonian and calculate the properties of the system in question by perturbation theory.
One thing we can not do is to continue past a symmetry boundary: the very obvious failure of analyticity of free energy at such boundary shows that this can not be done. It is also clear that two states of different symmetry can not be reached by simple continuation from the same state.
Theoretical methods
"Second" quantization
For many body system, an convenient formalism is developed. Defining operators which create or annihilate particles in specified states allows for much simpler bookkeeping, and more transparent physical interpretation, than the use of Slater determinants. Operators of physical interest may be expressed in terms of these creation and annihilation operators. It is noteworthy, and quite useful, that the eigenstates of annihilation operators are coherent states, a natural representation - the holomorphic representation.
Quantum Mechanics of a single particle
The state of a particle is described by a state vector , which belongs to a Hilbert space . Using Dirac notation, the scalar product of vectors in is:
Particularly, eigenvectors of the quantum position operator and momentum operator
A state vector represents a state in which the particle is localized at point , and a state vector represents a particle with a momentum . The overlap of these vectors is given by:
and
System of Identical Particles
The Hilbert space of states for a system of N identical particles is the space of complex, square integrable functions, defined in the configuration space of the N paticles. The wave function is , which represents the probability amplitude for finding particles at the N positions .
As we have defined it, the Hilbert, space is simply the tensor product of the single-particle Hilbert space :
If is an orthonormal basis of the canonical orthonormal basis of is constructed from the tensor products:
Note for future reference that the states defined in this way utilize a curved bracket in the ket symbol. These basis states have the wave functions:
The overlap of two vectors of the basis is given by:
and the completeness of the basis is obtained from the tensor product of the completeness relation far the basis :
where 1 now represents the unit operator in . Physjcally, it is clear that the space is generated by linear combinations of products of single-particle wave functions. Thus far, in defining the Hilbert space , we have not taken into account the symmetry property of the wave function. In contrast to the multitude of pure and mixed symmetry states one could define mathematically, only totally symmetric and antisymmetric states are observed in nature, Particles occurring in symmetric or antisymmetric states are called Bosons and Fermions respectively.
The wave function of N Bosons is totally symmetric and thus satisfies
where represents any permutation P of the set .
The wave function of N Fermions is antisymmetric under the exchange of any pair of particles and therefore satisfies:
Here, denotes the sign, or parity, of the permutation P, and is defined as the parity of the number of transpositions of two elements which brings the permutation to its original form .
Although the symmetry requirements for Bosons and Fermions are ultimately founded on experiment. It may be proven within the context of quantum field theory that given general assumptions of locality, causality and Lorentz invariance. Particles with integer spin (O,1,2, ...) are Bosons and particles with half-integer spin are Fermions. Familiar samples of Bosons include photons, pions, mesons, gluons,and the atom. Examples of Fermions include protons, neutrons, electrons, muons, neutrinos, quarks, and the atom. Composite particles composed of any number of Bosons and an even or odd number of Fermions behave as Bosons or Fermions respectively at energies sufficiently low compared to their binding energy.
For convenience, we shall adopt the following unified notation for Bosons or Fermions:
where P is the parity of the permutation, and is +1 or -1 for Bosons or Fermions respectively.
These symmetry requirements imply corresponding restrictions of the Hilbert space of N-particle systems. A wave function of belongs to the Hilbert space of N Bosons, , or the Hilbert space of N Fermions, . If it is symmetric or antisymmetric respectively, under a permutation of the particles.
We will define the symmetrization operator and the antisymmetrization operator in by their action on a wave function :
The manifestly Hermitian operator may be shown to be a projector as follows.
For any wave function of :
where P'P denotes the group composition of P' and P. Since , the summation over P and P' can be replaced by a summation over and P:
Using these project8cs, a system of Bosons or Fermions, with one particle in state , one particle in state , . . ., and oone particle in state , are represented as follows:
The scalar product of two such vectors constructed from the same basis is:
Because of the orthogonality of the basis , the only non-vanishing terms in the right hand side of equation above are the permutations P such that:
If is a permutation of , the overlap may be evaluated straightfowardly. For Fermions. since there is at most one particle per state , no two identical states can be present in the set and therefore, there exists only one permutation P which transforms into . The sum thus reduces to one term, and if the states are normalized, we obtain
( Fermions ) .
For Bosons, many particles may be in the same state, and therefore, any permutation which does interchange particles in the same state contributes to the sum. The overlap is thus equal to the total number of permutations which transform into . If the set of states represents a system with Bosons in state , Bosons in state , . . . , Bosons in state , where the states are distinct, the overlap is given by:
( Bosons ) .
Combining Fermions and Bosons together:
Thus, the orthonormal basis for Fermions and Bosons are:
Many-body Operators
We now consider matrix elements of many-body operators in the canonical basis of . From these, the representation of operators in the spaces and follows straightforwardly using the symmetrization and antisymmetrization operators .
let O be an arbitrary operator In Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_N} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_N} . Independent of whether the particles are Bosons or Fermions, their indistinguishability implies that O is invariant under any permutation of the particles. Thus, for any states, and any permutation P:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\beta_{P_1}...\beta_{P_N}|O|\beta'_{P_1}...\beta'_{P_N})=(\beta_{1}...\beta_{N}|O|\beta'_{1}...\beta'_{N})}
We begin by considering the care of one-body operators. An operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} is a one-body operator if the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} on a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N\rangle} of N particles is the sum of the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} on each particle:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}|\alpha_1...\alpha_N)=\sum^N_{i=1}\hat{U}_i|\alpha_1...\alpha_N)}
where the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}_i} operates only on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} particle.
The matrix element of a one-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}_i} between two states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\beta_1...\beta_N)} is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\alpha_1...\alpha_N|\hat{U}|\beta_1...\beta_N)=\sum^N_{i=1}(\alpha_1...\alpha_N|\hat{U}_i|\beta_1...\beta_N)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum^N_{i=1}\prod_{k\neq i}\langle \alpha_k|\beta_k\rangle \cdot \langle\alpha_i|\hat{U}|\beta_i\rangle}
Similarly, two-body operators may be expressed in terms of creation and annihilation operators. Two-body operators, i.e. operators which engage two-particles
E.g. symmetric pairwise interaction: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,x^{'})\equiv V(x^{'},x)}
(such as Coulomb) acting between two-particle states
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}=\frac{1}{2}\int dx\int dx^{'}\mid x,x^{'}>V(x,x^{'})<x,x^{'}\mid}
When acting on many-particle states,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}\mid x_{1},x_{2},...x_{N}>=\frac{1}{2}\sum_{n\neq m}^{N}V(x_{n},x_{m})\mid x_{1},x_{2},...x_{N}>}
How can one express ˆ V in second quantised form? We might guess that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}=\frac{1}{2}\int dx\int dx^{'}a^{+}(x)a^{+}(x^{'})V(x,x^{'})a(x^{'})a(x)}
i.e. annihilation operators check for presence of particles at x and x’ — if they exist, asign the potential energy and then recreate particles in correct order (viz. statistics). we use factor of two for double-counting.
check:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{+}(x)a^{+}(x^{'})V(x,x^{'})a(x^{'})a(x)\mid x_{1},x_{2},...x_{N}>=a^{+}(x_{1})a^{+}(x_{2})...a^{+}(x_{N})\mid\Omega>} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\Omega>} is the vaccum state.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{N}\zeta^{n-1}\delta(x-x_{n})a^{+}(x_{n})a^{+}(x^{'})a(x^{'})a^{+}(x_{1})...a^{+}(x_{n-1})a^{+}(x_{n+1})...a^{+}(x_{N})\mid\Omega>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{N}\zeta^{n-1}\delta(x-x_{n})\sum_{m(\neq n)}^{N}\delta(x^{'}-x_{m})a^{+}(x_{n})a^{+}(x_{1})...a^{+}(x_{n-1})a^{+}(x_{n+1})...a^{+}(x_{N})\mid\Omega>} where we used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{+}(x^{'})a(x^{'})=n(x^{'}).}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum_{n,m(\neq n)}^{N}\delta(x-x_{n})\delta(x^{'}-x_{m})\mid x_{1},x_{2},...x_{N}>}
then multiplying by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,x^{'})/2} , and integrate over x and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{'}} we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}} .
In general, we define an n-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}} as an operator which acts on a state in the following way:
That is, the action of on a state of N particles is the sum of the action of on all distinct subsets of n-particles. Analogous to the previous cases, the matrix elements of satisfy:
and an n-body operator is entirely determined by its matrix elements in the Hilbert space of n-particle systems.
Creation and Annihilation Operators
Creation and annihilation operators provide a convenient representation of the many-particle states and many-body operators introduced in the preceding sections. These operators generate the entire Hilbert space by their action on a single reference state and pravide a basis for the algebra of operators of the Hilbert space.
For each single-particle state of the single-particle space , we define a Boson or Fermion creation operator by its action on any symmetrized or antisymmetrized state of or as follows:
Coherent state path integrals
To define coherent states, annihilation operators are chosen, rather than creation operators.
Boson coherent states
Expand a boson coherent state in occupation number representation:
,
Set the eigenequation: .
Compare the above two equations, we get:
To satisfy this relation:
Recall ,
So we obtain:
.
Simplify it: , which is a standard form of boson coherent state.
Also:
Consider :
.
Also: .
Let us consider the overlap :
Since is not Hermitian operator, its eigenstates are not orthogonal.
Using ,
.
A crucial property of the Bosonic coherent states is their overcompleteness in the Fock space.
The unit operator in basis:
.
Proof:
Using ,
the method to prove the identity is to show that the l.h.s commutes with all creation and annihilation operators. Then it must be proportional to 1.
,
So, . (The last step is done through integration by parts. )
Similarly for .
So the l.h.s of the identity commutes with and for any .
.
Thus, we have proven the validity of this form of the unity operator.
The trace of one operator:
.
Grassmann Algebra
For fermions: ,
thus .
It will be necessary to use anticommuting numbers. Algebras of anticommuting numbers are called Grassmann algebras.
We first define Grassman algebra by associating each generator with an annihilation operator . Similarly, a generator is associated with each creation operator .
We then construct the generalized Fock space with coefficients in the Grassmann algebra:
,
where are grassman number and are vectors in Fock space.
The generators satisfy:
The basis of the Grassman algebra is made of all distinct products of the generators: , where by convention the indices are ordered . The dimension is .
Any object within the Grassmann algebra is a linear combination of these bases.
Conjugation:
In an algebra with even number of generators, we can define a conjugation operation, by selecting of generators and to each we associate a generator :
the following properties define conjugation in a Grassmann algebra,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\xi_{\alpha}^{*})^{*}=\xi_{\alpha}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\lambda\xi_{\alpha})^{*}=\lambda^{*}\xi_{\alpha}^{*}} .
For any product of generators: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\xi_{\alpha_{1}}...\xi_{\alpha_{n}}\right)^{*}=\xi_{\alpha_{n}}^{*}\xi_{\alpha_{n-1}}^{*}...\xi_{\alpha\phi_{1}}^{*}} .
Derivative:
As for ordinary complex functions, a derivative can be defined for grassmann variable functions. It is defined to be identical to the complex derivative, except that in order for the derivative operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}} to act on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} , the variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} has to be anti-commuted through until it is adjacent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}} .
ie.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}\xi=1; \frac{\partial}{\partial\xi}(\xi^{*}\xi)=-\xi; \frac{\partial}{\partial\xi}\lambda=0; \frac{\partial}{\partial\xi}(\xi\xi^{*})=\xi^{*}} ;
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \frac{\partial}{\partial\xi^{*}},\frac{\partial}{\partial\xi}\right\} =0.}
Integral:
We define integration over grassmann variable as a linear mapping which has the fundamental property of order integrals over functions vanishing at infinity that the integral of an exact differential form is zero:
so: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi1=0} , and we define:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi\xi=1.}
also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}1=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}\xi^{*}=1} .
Grassmann Delta function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(\xi,\xi')=\int d\eta e^{-\eta(\xi-\xi')}=\int d\eta(1-\eta(\xi-\xi')).}
Prove: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi'\delta(\xi,\xi')f(\xi')=\int d\xi'\int d\eta(1-\eta(\xi-\xi'))f(\xi')=f(\xi).}
Scalar product of Grassmann functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle f|g\right\rangle =\int d\xi^{*}d\xi e^{-\xi^{*}\xi}f^{*}(\xi)g(\xi^{*})} ,
Since Grassmann numbers anticommute, any function of Grassmann numbers can only be expanded to the 1st order:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\xi)=f_{0}+f_{1}\xi, g(\xi)=g_{0}+g_{1}\xi} ,
and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle f|g\right\rangle =f_{0}^{*}g_{0}+f_{1}^{*}g_{1}.}
Fermion coherent states
In order to construct coherent states, we must enlarge the Fermion Fock space.
Define a Grassmann algebra Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{G}} .
The difference from boson coherent states is due the necessary coefficients. For bosons, we may use only c-numbers, but for fermions it is necessary to use Grassmann numbers, so that the anticommutation relations will be preserved.
Any vector in the generalized Fock space is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi\right\rangle =\underset{\alpha}{\sum}\chi_{\alpha}\left|\phi_{\alpha}\right\rangle .}
We need to treat expressions containing combinations of Grassmann variables and creation and annihilation operators. So, we define: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \overset{\sim}{\xi},\overset{\sim}{a}\right\} =0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\overset{\sim}{\xi}\overset{\sim}{a})^{\dagger}=\overset{\sim}{a}^{\dagger}\overset{\sim}{\xi}^{*}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{\xi}} denotes any Grassmann variable in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \xi_{\alpha},\xi_{\alpha}^{*}\right\}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{a}} denotes any operator in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ a_{\alpha},a_{\alpha}^{\dagger}\right\} } .
Define a fermion coherent state: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\xi\right\rangle =e^{\underset{\alpha}{-\sum}\xi_{\alpha}a_{\alpha}^{_{\dagger}}}\left|0\right\rangle =\underset{\alpha}{\prod}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle } .
Although the coherent state belongs to the generalized Fock space and not to \mathcal{F}, as we shall see, the crucial point is that any physical Fermion state of \mathcal{F} can be expanded in terms of these coherent states.
Proof that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\xi\right\rangle } is the eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}:}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle =\xi_{\alpha}a_{\alpha}a_{\alpha}^{_{\dagger}}\left|0\right\rangle =\xi_{\alpha}(\left\{ a_{\alpha},a_{\alpha}^{\dagger}\right\} -a_{\alpha}^{\dagger}a_{\alpha})\left|0\right\rangle =\xi_{\alpha}\left|0\right\rangle =\xi_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle } .
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}\left|\xi\right\rangle =a_{\alpha}\underset{\beta}{\prod}(1-\xi_{\beta}a_{\beta}^{_{\dagger}})\left|0\right\rangle } .
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\neq\beta} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [1-\xi_{\alpha}a_{\alpha}^{_{\dagger}},1-\xi_{\beta}a_{\beta}^{_{\dagger}}]=\xi_{\alpha}a_{\alpha}^{_{\dagger}}\xi_{\beta}a_{\beta}^{_{\dagger}}-\xi_{\beta}a_{\beta}^{_{\dagger}}\xi_{\alpha}a_{\alpha}^{_{\dagger}}=0,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_{\alpha},1-\xi_{\beta}a_{\beta}^{_{\dagger}}]=0,}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow a_{\alpha}\left|\xi\right\rangle =\underset{\beta\neq\alpha}{\prod}(1-\xi_{\beta}a_{\beta}^{_{\dagger}})a_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle =\xi_{\alpha}\left|\xi\right\rangle .}
The adjoint of the coherent state: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi\right|=\left\langle 0\right|e^{\underset{\alpha}{-\sum}a_{\alpha}\xi_{\alpha}^{*}}=e^{\underset{\alpha}{\sum}\xi_{\alpha}^{*}a_{\alpha}},} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi\right|a_{\alpha}^{\dagger}=\left\langle \xi\right|\xi_{\alpha}^{*}.}
The action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger} } on a coherent state:
similarly,
The overlap of the two coherent states (It is very important to remember that this is not Unity!):
.
Unit operator:
This is the unit operator in the physical Fermion Fock space .
Proof:
Define operator
,
since all the states s are either occupied in both and or unoccupied in both states. This requires and is some permutation of So write After this, all the necessary changes commute.
So and the equality is established for any vectors in the Fock space.
Trace:
.
Gaussian Integrals
Here we prove 3 Identities for for multidimensional Gaussian integrals over 3 different kinds of variables:
where are real variables and A is a real symmetric positive definite matrix. Summation over repeated indices is used throughout this subsection.
where are complex variables and H is a positive Hermitian matrix.
where and are Grassmann variables and H is a Hermitian but not necessary positive definite matrix.
Proof of GI1
The idea is making change of variables so that the matrix reduces to diagonal form and then we can use the familiar Gaussian Integral
to obtain the result. we first perform transformation , and then
where is orthogonal transformation which diagonalize with eignvalues . So we have
Note that the positivity of A is essential for the convergence of the Gaussian integral.
Proof of GI2
Following similar idea. First perform transformation
, and then
where is orthogonal transformation which diagonalize H with eignvalues . So we have
Proof of GI3
First we note that the Gaussian integral involving a single pair of conjugate Grassmann variable is evaluated as follow:
Note that for single variable, the Gaussian integral involve in contrast to as we obtain in original Gaussian integral. So if we could bring the multi-variable Gaussian integral into diagonal form, we would expect to get a similar result involving the product of the eigenvalues, and thus the determinant of H, in the numerator instead of the denominator as for complex variables.
Second, we need to derive the law for the linear transformation of Grassmann variables. Assume
Relabel the variables as
writing
Since the only non-vanishing terms in the integral come from the term containing every as a factor one times, so we can write
So we rewrite the integral as
So we get
So the linear transformation law for Grassmann variable is
which is different from the transformation law for complex variable by the appearance of the inverse of the Jacobian instead of Jacobian.
Now to prove GI3, we perform transformation
Then diagonalizing H with unitary transformation and define
Linear response and Green's function
Linear response
Consider a system defined with a Hamiltonian that we assume is time-independent, and then add an interaction term as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=H_{0}+U(t)O_{1}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{1}} is an operator associated to the external field U(t). Then we are looking for the response of the system to this field. This is found by calculating the average of another operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}} . For example in an external magnetic field first operator could be spin operator and the next operator (which is averaged over to find the system response) is the magnetic moment of the system.
Now, imagine that the system is described not by a pure state at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=t_{0}} , but by a density matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _{0}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _{0}=\frac{1}{Tr e^{-\beta(H_{0}-\mu N)}}\sum_{n}\mid n>e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid}
So we can calculate average of any operator by using of this density matrix. For example for operator R we can say: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{R}>=Tr(\hat{\rho _{0}}\hat{R})} If we want to define density operator in later time(t), only we need to use the evolution operator to create that like this: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho _{t}}=\frac{1}{Tr e^{-\beta\hat{(H_{0}}-\mu \hat{N})}}\sum_{n}\hat{u}(t,t_{0})\mid n>e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid \hat{u}^{-1}(t,t_{0})}
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=Tr(\hat{\rho _{t}}\hat{O_{2}})=\frac{1}{Z}\sum_{n}e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid \hat{u}^{-1}(t,t_{0})\hat{O_{2}}\hat{u}(t,t_{0})\mid n>}
Where Z is the partition function that is as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\frac{1}{Tr e^{-\beta\hat{(H_{0}}-\mu \hat{N})}}} . So in the next step we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=\frac{1}{Z}Tr( \hat{u}^{-1}(t,t_{0})\hat{O_{2}}\hat{u}(t,t_{0})e^{-\beta (\hat{H_{0}}-\mu \hat{N})})}
In general this result is a complicated, nonlinear f unction of U(t). In linear response theory we are interested in the right-hand side for vanishing small values of U(t). As we know in the Heisenberg picture we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial }{\partial t}\hat{u}(t,t_{0})=(H_{0}+U(t)O_{1}))\hat{u}(t,t_{0})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{u}(t,t_{0})=e^{\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}\hat{u}(t,t_{0})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{u}(t,t_{0})=1+\frac{1}{i\hbar}\int_{t_{0}}^{t}d{t}'U({t}')e^{\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}\hat{O_{1}}e^{-\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}+...}
If we substitute this result in the average of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}} after some simple calculations we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=\frac{1}{Z}Tr(\hat{O_{2}}e^{-\beta (\hat{H_{0}}-\mu \hat{N})}))+\frac{1}{i\hbar}\frac{1}{Z}\int_{-\infty}^{\infty}d{t}'U({t}')Tr([\hat{O}^{(H)}_{2}(t),\hat{O}^{(H)}_{1}(t)]e^{-\beta (\hat{H_{0}}-\mu \hat{N})})\theta (t-{t}')}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{O}^{(H)}_{2}(t)} shows that we work in the Heisenberg picture. First term is related to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{0}} and we usually consider it equal to zero.
now we try to calculate the partition function for many particle systems:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\frac{1}{Tr e^{-\beta\hat{(H}-\mu \hat{N})}}=\int \prod_{\alpha }\frac{d\phi^{*} _{\alpha }d\phi _{\alpha }}{N}e^{-\sum_{\alpha }\phi^{*} _{\alpha }\phi _{\alpha}}<\xi \phi \mid e^{-\beta\hat{(H}-\mu \hat{N})}\mid \phi >}
Partition function for many particle system
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=Tr[e^{-\beta(\hat{H}-\mu\hat{N})}]} , now we expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta=\epsilon M} , and take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon\rightarrow 0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\rightarrow\infty} , therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } evolves as “imaginary time”:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta(\hat{H}-\mu\hat{N})}=e^{-\epsilon(\hat{H}-\mu)}\mathbb{I}e^{-\epsilon(\hat{H}-\mu)}\mathbb{I}...\mathbb{I}e^{-\epsilon(\hat{H}-\mu)}} ,
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}=\int\prod_{\alpha}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{N}e^{-\sum_{\alpha}\phi_{\alpha}^{*}\phi_{\alpha}}<\xi|\xi>} .
here are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M-1} terms sandwiched between the imaginary time slicing. A generic term will look like
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi_{k+1}|1-\epsilon(\hat{H}-\mu\hat{N})+\mathcal{O}(\epsilon^{3})|\phi_{k}\right\rangle =\left\langle \phi_{k+1}|1-\epsilon(H-\mu N)(\phi_{k+1}^{*},\phi_{k})+\mathcal{O}(\epsilon^{3})|\phi_{k}\right\rangle} ,
the left hand side is already in normal order.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =e^{-\epsilon(H-\mu N)}(\phi_{k+1}^{*},\phi_{k})\left\langle \phi_{k+1}|\phi_{k}\right\rangle +\mathcal{O}(\epsilon^{3})} .
Now we calculate:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \zeta\phi|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi\right\rangle =\int\prod_{k=1}^{M-1}\prod_{\alpha}\frac{d\phi_{\alpha,k}^{*}d\phi_{\alpha,k}}{N}e^{-\sum_{k=1}^{M-1}\sum_{\alpha}\phi_{\alpha,k}^{*}\phi_{\alpha,k}}\left\langle \zeta\phi|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{M-1}\right\rangle \left\langle \phi_{M-1}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{M-2}\right\rangle ...\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi_{2}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{1}\right\rangle \left\langle \phi_{1}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi\right\rangle >=\int\prod_{k=1}^{M-1}\prod_{\alpha}\frac{d\phi_{\alpha,k}^{*}d\phi_{\alpha,k}}{N}e^{-\sum_{k=1}^{M-1}\sum_{\alpha}\phi_{\alpha,k}^{*}\phi_{\alpha,k}}e^{-\sum_{\alpha}\zeta\phi_{\alpha,1}^{*}\phi_{\alpha,M-1}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{1}^{*},\phi_{M-1})}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\sum_{\alpha}\phi_{\alpha,M-1}^{*}\phi_{\alpha,M-2}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{M-1}^{*},\phi_{M-2})}...e^{-\sum_{\alpha}\phi_{\alpha,1}^{*}\phi_{\alpha}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{1}^{*},\phi)}}
Because each of the terms containing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} commute , we can write as exponent of sums: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon\sum\{\phi_{\alpha,M}^{*}\frac{\left(\phi_{\alpha,M-1}^{*}-\phi_{\alpha,M}\right)}{\epsilon}+\phi_{\alpha,M-1}^{*}\frac{\left(\phi_{\alpha,M-2}^{*}-\phi_{\alpha,M-1}\right)}{\epsilon}+...+\phi_{\alpha,1}^{*}\frac{\left(\phi_{\alpha,0}^{*}-\phi_{\alpha,1}\right)}{\epsilon}-\left[H\phi_{\alpha,M}^{*}\zeta\phi_{\alpha,M-1}-\mu\phi_{\alpha,M}^{*}\zeta\phi_{\alpha,M-1}\right]-} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[H\phi_{\alpha,M-1}^{*}\zeta\phi_{\alpha,M-2}-\mu\phi_{\alpha,M-1}^{*}\zeta\phi_{\alpha,M-2}\right]-...-\left[H\phi_{\alpha,1}^{*}\zeta\phi_{\alpha,M}-\mu\phi_{\alpha,1}^{*}\zeta\phi_{\alpha,M}\right]\}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta\phi_{\alpha,M}=\phi_{\alpha,0}} . This looks like a Reimann Sum. At each time slice, involve product over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha}^{*}\phi_{\alpha}} . By using the notation that:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial \tau} \phi_{\alpha,M} = \frac{\phi_{\alpha, M-1} - \phi_{\alpha,M}}{\epsilon} }
The complicated integral of Operator and states reduces into :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}-\mu\right)\phi_{\alpha}(\tau)+H(\phi_{\alpha}^{*}(\tau),\phi_{\alpha}(\tau))\right]}}
Note that the differential notation above is not exactly correct; there is no necessary condition that the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha,i}} 's be continuous in any sense. It turns out that the continuum representation is quite useful, but at times must be discarded in favor of the exact meaning.
Thermal(imaginary-time) Green's function
Now, We define Thermal(imaginary-time) Green's function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{(n)}(\alpha_{1}\tau_{1},...,\alpha_{n}\tau_{n}\mid\alpha_{1}^{'}\tau_{1}^{'},...,\alpha_{n}^{'}\tau_{n}^{'})=<T_{\tau}[a_{\alpha_{1}}^{(H)}(\tau_{1}).....a_{\alpha_{n}}^{(H)}(\tau_{n})a_{\alpha_{n}^{'}}^{(H)^{+}}(\tau_{n}^{'}).....a_{\alpha_{1}^{'}}^{(H)^{+}}(\tau_{1}^{'})]> } Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha^{'}}^{(H)^{+}}(\tau^{'})\equiv e^{\tau(H-\mu N)}a_{\alpha}^{+}e^{-\tau(H-\mu N)}} , so that these operators are not Hermitian anti conjugate of each other.
and is the time ordering operator and it is defined as
For example for two operators:
for or it equals to so that the upper sign is for Bosons and the lower sign is for Fermions.
So we can write the green's function as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{Z}Tr[e^{-\beta(H-\mu N)}\xi^{p} \tilde{a}_{\alpha_{p1}}^{(H)}(\tau_{p1})} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{a}_{\alpha_{p2}}^{(H)}....\tilde{a}_{\alpha_{p2n}}^{(H)}(\tau_{p2n})}
Where p is the permutation which gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{p1}>\tau_{p2}>....>\tau_{p2n}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{a}_{j}=a_{j} , \tilde{a}_{j+n}^{+}=a_{j}^{+}for j=1,...,n. } Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{(n)}(\alpha_{1}\tau_{1},...,\alpha_{n}\tau_{n}\mid\alpha_{1}^{'}\tau_{1}^{'},...,\alpha_{n}^{'}\tau_{n}^{'})=\frac{\xi^{p}}{Z}Tr[e^{-\beta(H-\mu N)}e^{\tau_{p1}(H-\mu N)}\tilde{a}_{\alpha_{p1}}e^{-\tau_{p1}(H-\mu N)}...]}
If again slice up all exponential terms we will have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\xi^{p}}{Z}Tr[e^{-\int_{\tau_{p1}}^{\beta}d\tau^{'}(H-\mu N)}\tilde{a}_{\alpha_{p1}}e^{-\int_{\tau_{p2}}^{\tau_{p1}}d\tau^{'}(H-\mu N)}\tilde{a}_{\alpha_{p2}}...e^{-\int_{0}^{\tau_{p2n}}d\tau^{'}}]\frac{\xi^{p}}{Z}\int D[\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)]e^{-\int_{0}^{\beta}d\tau L(\tau)}\tilde{\Phi}_{\alpha_{p1}}(\tau_{p1})\tilde{\Phi}_{\alpha_{p2}}(\tau_{p2})....\tilde{\Phi}_{\alpha_{p2n}}(\tau_{p2n})}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(\tau)=\sum_{\alpha}([\Phi(\tau)(\frac{\partial}{\partial\tau}-\mu)\Phi_{\alpha}(\tau)+H(\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)]}
Let's calculate the partition function of free bosons/fermions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{\alpha}\varepsilon_{\alpha}a_{\alpha}^{+}a_{\alpha}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(\tau)==\sum_{\alpha}([\Phi(\tau)(\frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha}(\tau)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau L(\tau)=\sum_{\alpha}(\sum_{k=2}^{m}\Phi_{\alpha,k}^{*}(\Phi_{\alpha,k}-\Phi_{\alpha,k-1}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\Phi_{\alpha,k-1})+\Phi_{\alpha,1}^{*}(\Phi_{\alpha,1}-\xi\Phi_{\alpha,m}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\xi\Phi_{\alpha,m}))}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=lim_{m\rightarrow\infty}\prod_{\alpha}(\int\prod_{k=1}^{m}\frac{d\Phi_{k}^{*}d\Phi_{k}}{N}e^{-\Phi_{i}^{*}S_{ij}^{(\alpha)}\Phi_{j}})}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{ij}^{(\alpha)}=\left(\begin{array}{ccccc} 1 & 0 & .... & .. & -\xi\lambda\\ -\lambda & 1 & 0 & ... & 0\\ 0 & -\lambda & 1 & 0.... & 0\\ ... & .. & -\lambda & .. & ..\\ .. & .. & .. & -\lambda & 1\end{array}\right)_{m\times m} and \lambda=1-\frac{\beta}{m}(\varepsilon_{\alpha}-\mu).}
So we can calculate the partition function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=lim_{m\rightarrow\infty}\prod_{\alpha}(Det(S_{ij}^{(\alpha)}))^{-\xi}=\prod_{\alpha}lim_{m\rightarrow\infty}(1-\xi\lambda^{m})^{-\xi}=\prod_{\alpha}(1-\xi e^{-\beta(\varepsilon_{\alpha}-\mu)})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\begin{cases} \begin{array}{cc} \prod_{\alpha}\frac{1}{1-e^{-\beta(\varepsilon_{\alpha}-\mu)}} & boson\\ \prod_{\alpha}(1+e^{-\beta(\varepsilon_{\alpha}-\mu)}) & fermions\end{array}\end{cases}}
Moreover, we can get the same result if we work in k-space and use the Fourier transformation for functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\alpha}(\tau)=\frac{1}{\beta}\sum_{m}e^{-i\omega_{n}\tau}\Phi_{\alpha,i\omega_{n}}} , that we use the Hatsubara frequencies for bosons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{n}=\frac{2n\pi}{\beta}} and for fermions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{n}=\frac{(2n+1)\pi}{\beta}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0,\pm1,\pm2,....}
Example: calculation of thermal Green's function for two operator
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a^{+(H)}(\tau)>=\frac{1}{Z}\int D[\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)]\Phi_{\alpha}(\tau)\Phi_{\beta}^{*}(\tau^{'})e^{-S}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\sum_{\alpha}\frac{1}{\beta}\sum_{\omega_{n}}\Phi_{\alpha,i\omega_{n}}^{*}(-i\omega_{n}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha,i\omega_{n}}} .
If we use the Fourier transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\alpha}(\tau)=\frac{1}{\beta}\sum_{m}e^{-i\omega_{n}\tau}\Phi_{\alpha,i\omega_{n}}} so we will have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\beta^{2}}\sum_{i\omega_{n},i\nu_{n}}e^{-i\omega_{n}\tau}e^{i\nu_{n}\tau^{'}}\frac{1}{Z}\int D[\Phi_{\alpha}^{*}(i\omega_{n}),\Phi_{\alpha}(i\nu_{n})]\Phi_{\alpha,i\omega_{n}}\Phi_{\beta,i\nu_{n}}^{*}e^{-\sum_{\alpha}\Phi_{\alpha,i\omega_{n}}^{*}L{}_{\alpha}\Phi_{\alpha,i\omega_{n}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}\xi\frac{\partial}{\partial J_{\beta,i\nu_{n}}}\frac{1}{Z}\int D[\Phi_{\alpha}^{*}(i\omega_{n}),\Phi_{\alpha}(i\nu_{n})]e^{-S}e^{J_{\alpha,i\omega_{n}}^{*}\Phi_{\alpha,i\omega_{n}}}e^{\Phi_{\beta,i\nu_{n}}^{*}J_{\beta,i\nu_{n}}}\mid_{J=J^{*}=0}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}\xi\frac{\partial}{\partial J_{\beta,i\nu_{n}}}\frac{(DetL_{\alpha})^{-\xi}}{(DetL_{\alpha})^{-\xi}}e^{J_{\alpha,i\omega_{n}}^{*}(\frac{1}{L})J)\alpha,i\omega_{n}}\mid_{J=J^{*}=0}=\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}J_{\beta,i\nu_{n}}^{*}\frac{1}{L_{\alpha}}e^{J_{\alpha,i\omega_{n}}^{*}(\frac{1}{L})J_{\alpha,i\omega_{n}}}\mid_{J=J^{*}=0}=\delta_{\alpha,\beta}\delta_{\omega_{n,\nu_{n}}}\frac{1}{L_{\alpha}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\delta_{\alpha,\beta}\delta_{\omega_{n,\nu_{n}}}\frac{\beta}{-i\omega_{n}+\varepsilon_{\alpha}-\mu}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{\alpha}=\frac{1}{\beta}(-i\omega_{n}+\varepsilon_{\alpha}-\mu)} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a_{\beta}^{+^{(H)}}(\tau^{'})>=\delta_{\alpha\beta}\frac{1}{\beta}\sum_{i\omega_{n}}e^{-i\omega_{n}(\tau-\tau^{'})}\frac{1}{-i\omega_{n}+\varepsilon_{\alpha}-\mu}}
We check this result for two different cases:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a)\tau\leq\tau^{'} : \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\oint\frac{dz}{2\pi i}\frac{e^{-z(\tau-\tau^{'})}}{z-(\varepsilon_{\alpha}-\mu)}\frac{-1}{e^{\beta z}+1}=\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{\beta(\varepsilon_{\alpha}-\mu)}+1}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b)\tau>\tau^{'} : \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\oint\frac{dz}{2\pi i}\frac{e^{-z(\tau-\tau^{'})}}{z-(\varepsilon_{\alpha}-\mu)}\frac{1}{e^{-\beta z}+1}=\frac{-e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{-\beta(\varepsilon_{\alpha}-\mu)}+1}}
So in general we have :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\Theta(\tau^{'}-\tau+\eta)\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{\beta(\varepsilon_{\alpha}-\mu)}+1}-\Theta(\tau^{'}-\tau-\eta)\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{-\beta(\varepsilon_{\alpha}-\mu)}+1}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =e^{-(\tau-\tau^{'})(\varepsilon_{\alpha}-\mu)}([n(\varepsilon_{\alpha}-\mu)\Theta(\tau^{'}-\tau+\mu)+(n_{f}(\varepsilon_{\alpha}-\mu)-1)\Theta(\tau-\tau^{'}-\eta)]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a_{\beta}^{+^{(H)}}(\tau^{'})>=\delta_{\alpha\beta}e^{-(\tau-\tau^{'})(\varepsilon_{\alpha}-\mu)}([\mp n(\varepsilon_{\alpha}-\mu)\Theta(\tau^{'}-\tau+\mu)+(1\mp n_{f}(\varepsilon_{\alpha}-\mu))\Theta(\tau-\tau^{'}-\eta)]}
Where the upper sign is for fermions and the lower sign is for bosons.
We may obtain this directly as an inverse ofFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\eta} by solving
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\eta)G(\alpha\tau,\alpha\tau^{'})=\delta(\tau-\tau^{'})}
subject to the bounding condition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\alpha\beta,\alpha\tau^{'})=\xi G(\alpha0,\alpha\tau^{'})} .
The Green function of the phonons is usually denoted by D. The definition of this function is similar to the previous one as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(t-t^{'})=-\frac{i}{\hbar}\Theta(t-t^{'})<[O_{2}^{(H)}(t),O_{1}^{(H)}(t^{'})]>} for real time,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}^{(H)}(t)=e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}} .
and for imaginary time is as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D_{12}}(\tau-\tau^{'})=-<T_{\tau}O_{2}^{(H)}(\tau),O_{1}^{(H)}(\tau^{'})>where O_{2}^{(H)}(\tau)=e^{\tau(H_{0}-\mu N)}O_{2}e^{-\tau(H_{0}-\mu N)}} .
Now we try to connect these two different Green's function to each other. First we start with real time
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar}{i}D_{12}^{R}(t-t^{'})\Theta(t-t^{'})=\frac{1}{Z}Tr[e^{-\beta(H_{0}-\mu N0}(e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}e^{\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}O_{1}e^{-\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}-}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}O_{1}e^{-\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}]}
In the eigenstate basis we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n}e^{-\beta(E_{n}-\mu N)}(e^{\frac{i}{\hbar}E_{n}(t-t^{'})}<n\mid O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t^{'})}O_{1}\mid n>....)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n,m}e^{-\beta(E_{n}-\mu N)}(e^{\frac{i}{\hbar}(E_{n}-E_{m})(\tau-\tau^{'})}<n\mid O_{2}\mid m><m\mid O_{1}\mid n>-e^{\frac{i}{\hbar}(E_{m}-E_{n})(\tau-\tau^{'})}<m\mid O_{2}\mid n><n\mid O_{1}\mid m>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n,m}(e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)})e^{\frac{i}{\hbar}(E_{n}-E_{m})(t-t^{'})}<n\mid O_{2}\mid m><m\mid O_{1}\mid n>}
Then we use the Fourier transformation for this result Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(\Omega)=\int_{-\infty}^{+\infty}dte^{i\Omega t}D_{12}^{R}(t)} and also a definition for Teta function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta(t)=\frac{1}{2\pi i}\int_{-\infty}^{+\infty}d\nu\frac{e^{i\nu t}}{\nu-i\eta}} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(\Omega)=\int_{-\infty}^{+\infty}\frac{d\nu}{2\pi i}\int_{-\infty}^{+\infty}dte^{i\Omega t}e^{i\nu t}(-\frac{i}{\hbar})\frac{1}{\nu-i\eta}\frac{1}{Z}\sum_{n,m}(e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)})e^{\frac{i}{\hbar}(E_{n}-E_{m})(t-t^{'})}<n\mid O_{2}\mid m>\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <m\mid O_{1}\mid n>=-\frac{i}{\hbar})\frac{1}{Z}\sum_{n,m}\frac{1}{2\pi i}\frac{2\pi}{-\Omega-\frac{E_{n}E_{m}}{\hbar}-i\eta}(e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)})<n\mid O_{2}\mid m><m\mid O_{1}\mid n>} And now we calculate the imaginary time
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D_{12}}(\tau)=-<O_{2}^{(H)}(\tau)O_{1}^{(H)}(0)>=\frac{-1}{Z}Tr[e^{-\beta(H_{0}-\mu N)}e^{\tau(H_{0}-\mu N)}O_{2}e^{-\tau(H_{0}-\mu N)}O_{1}]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{Z}\sum_{n,m}e^{-\beta(E_{n}-\mu N)}e^{\tau(E_{n}-\mu N)}<n\mid O_{2}\mid m>e^{-\tau(E_{m}-\mu N)}<m\mid O_{1}\mid n>}
If we again go to the Fourier space, we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}_{12}^{'}(i\Omega_{n})=\int_{0}^{\beta}d\tau e^{i\Omega_{n}\tau}\overline{D}_{12}(\tau)=\frac{-1}{Z}\sum_{n,m}\frac{e^{-\beta(E_{m}-\mu N)}-e^{-\beta(E_{n}-E_{m})}}{E_{n}-E_{m}+i\Omega_{n}}<n\mid O_{2}\mid m><m\mid O_{1}\mid n>}
So we conclude that two functions are the same if we only change Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\Omega_{n}\rightarrow\hbar(\Omega+i\eta)} in imaginary time function. In another words,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}_{12}(i\Omega_{n}\rightarrow\hbar(\Omega+i\eta))=D_{12}^{R}(\Omega)}
Now we like to study real time Green's function and its properties:
Definition.
Free particle Green functions
One of the most important characteristics of the microscopic properties of a system in quantum field theory is the one-particle Green function. It is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha\beta}(x,x^{'})=-i<T(\tilde{\psi}_{\alpha}(x)\tilde{\psi}_{\beta}^{+}(x^{'}))>}
We understand by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} (or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} ) a set of four variables :the coordinates r and the time I; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} are the spin indices.
As we know the one-particle operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}} may be written in the new representation in the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}=\int\psi^{+}(\xi)f^{1}\psi(\xi)d\xi} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} is the field operator.A knowledge of the Green function enables us to find the average over the ground state of any one-particle operator.Indeed, we have from
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}=\pm i\int[lim_{t^{'}\rightarrow t,r\rightarrow r^{'}}f_{\alpha\beta}^{1}(x)G_{\alpha\beta}(x,x^{'})]d^{3}r}
(the plus (minus) sign for Bose (Fermi) statistics). For instance, the density of the number of particles and the particle flux density are, respectively, equal to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(x)=\pm ilim_{t^{'}\rightarrow t,r\rightarrow r^{'}}G_{\alpha\alpha}(x,x^{'})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j(x)=\pm\frac{1}{2m}lim_{t^{'}\rightarrow t,r\rightarrow r^{'}}(\nabla_{r}-\nabla_{r^{'}})G_{\alpha\alpha}(x,x^{'})}
Green's functions originate in the question, "Starting with a particle at site Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0)} at time 0, what is the amplitude for finding it at site Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R)} at time f ?." The answer to this question is that the amplitude is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <R\mid G(t)>\mid0>=<R\mid e^{\frac{-i\hat{H}t}{\hbar}}\mid0>} .
It is more convenient to work with Fourier transform of this operator, so define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\varepsilon)=\frac{1}{i\hbar}\int_{0}^{\infty}dte^{\frac{i(\varepsilon+i\delta)t}{\hbar}}G(t)\Rightarrow G(\varepsilon)=(\varepsilon-\hat{H}+i\delta)^{-1}}
where to make the integrals converge, we need to add the infinitesimal quantity i\delta to the exponents. sometimes, we consider energy in the complex plane and so we do not need to consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\delta} in that case. this fact warns that the physical significance of Green's functions may depend in an important way on the complex part of the energy, even when it is very small.
So Green's function contains full information about the time evolution of a particle: When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} and energy has a positive imaginary part, the information is about the future, and when \delta has a negative imaginary part, the information is about the past. As you can see the above formula shows that Green's function has a pole whenever \hat{H} has an eigenvalue, because if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\varepsilon_{n}>} are the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}} with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{n}} , then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\varepsilon)=(\varepsilon-\hat{H})^{-1}=\sum_{n}(\varepsilon-\hat{H})^{-1}\mid\varepsilon_{n}><\varepsilon_{n}\mid=\sum_{n}\frac{\mid\varepsilon_{n}><\varepsilon_{n}\mid}{\varepsilon-\varepsilon_{n}}} .
Let assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon=\varepsilon_{r}\pm i\eta} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{r}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} real, if we expand Green's function in the neighborhood of the poles we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{\pm}(\varepsilon)\sim\frac{\mid\varepsilon_{n}><\varepsilon_{n}\mid(\varepsilon_{r}-\varepsilon_{n})}{(\varepsilon_{r}-\varepsilon_{n})^{2}+\eta^{2}}\mp\frac{i\eta\mid\varepsilon_{n}><\varepsilon_{n}\mid}{(\varepsilon_{r}-\varepsilon_{n})^{2}+\eta^{2}}=\mid\varepsilon_{n}><\varepsilon_{n}\mid\{\frac{1}{\varepsilon_{r}-\varepsilon_{n}}\mp i\pi\delta(\varepsilon_{r}-\varepsilon_{n})\}}
Where we used this point that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is very small and positive Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi\delta(x)=\frac{\eta}{(x^{2}+\eta^{2})}} .
The imaginary part of G keeps track of the density of states. In particular,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mp\frac{1}{\pi}Im[<R\mid G^{\pm}(\varepsilon)\mid R>]=\sum_{n}\delta(\varepsilon_{r}-\varepsilon_{n})\mid<R\mid n>\mid^{2}}
defines the local density of states at position R.
diagramatic perturbation theory and fluctuation dissipation theorem
Diagramatic perturbation theory
In this section, we consider the case of a Hamiltonian which has been decomposed into the sum of a one-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}} and the residual Hamiltonian V, which in general may contain a one-body interaction as well as many-body interactions, and develop a systematic perturbation expansion in powers of V. The basis will be chosen to diagonalize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}=\sum_{\alpha}\varepsilon_{\alpha}a_{\alpha}^{+}a_{\alpha}} and we will write the normal-ordered many-body part a as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(a_{\alpha}^{+}a_{\beta}^{+}...a_{\gamma}a_{\delta}..)} .
For example for a 3D electron gas in an external magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(r,t)} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\int d^{3}r(\sum_{\sigma}\psi_{\sigma}^{+}(r)(\frac{p^{2}}{2m}-\mu)\psi_{\sigma}(r)-\mu_{B}H(r,t)\psi_{\sigma}^{+}(r)\psi_{\sigma}(r))}
To calculate the average of magnetic momentum, we first calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})} in imaginary time and then we calculate real time Green's function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=-<T_{\tau}(\psi_{\alpha}^{+}\sigma_{\alpha\beta}^{z}\psi)^{(H)}(\psi_{\gamma}^{+}\sigma_{\gamma\delta}\psi_{\delta})^{(H)}} >
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{Z}\int D[\Phi_{\sigma}^{*}(r,\tau),\Phi_{\sigma}(r,\tau)]\Phi_{\alpha}^{*}(r,\tau),\sigma_{\alpha\beta}^{z}\Phi_{\beta}(r,\tau)\Phi_{\gamma}^{*}(r^{'},\tau^{'})\sigma_{\gamma\delta}^{z}\Phi_{\delta}(r^{'},\tau')e^{-S}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\int_{0}^{\beta}d\tau\int d^{3}r\Phi_{\sigma}^{*}(r,\tau)(\frac{\partial}{\partial\tau}+\frac{p^{2}}{2m}-\mu)\Phi_{\sigma}(r,\tau)} .
In general potential we can expand in power series and then like this case we get an integral like Gaussian integral but some powers in front of it. For this case we have a very useful theorem that we like to introduce here.
Wick's Theorem
In the form we will use it, Wick's theorem corresponds to the following identity for the integral of a product of a polynomial with a Gaussian
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\int D[\xi^{*},\xi]\xi_{i1}\xi_{i2}...\xi_{in}\xi_{jn}^{*}...\xi_{j2}^{*}\xi_{j1}^{*}e^{-\sum_{i,j}\xi_{i}^{*}M_{i,j}\xi_{j}}}{\int D[\xi^{*},\xi]e^{-\sum_{i,j}\xi_{i}^{*}M_{i,j}\xi_{j}}}=\sum_{p}\xi^{p}M_{ip_{n},j_{n}}^{-1}M_{ip_{n-1},j_{n-1}}^{-1}...M_{ip_{1},j_{1}}^{-1}}
to prove this theorem, we assume a generating function like below that we know its value:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(J^{*},J)=\frac{\int D(\xi^{*},\xi)e^{-\sum_{i,j}\xi_{i}^{*}M_{i,j}\xi_{j}}e^{\sum_{i}(J_{i}^{*}\xi_{i}+\xi_{i}^{*}J_{i})}}{\int D(\xi^{*},\xi)e^{-\sum_{i,j}\xi_{i}^{*}M_{i,j}\xi_{j}}}=e^{\sum_{i,j}J_{i}^{*}M_{i,j}^{-1}J_{j}}}
Now, we derivative from both sides and then put Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=J^{*}=0} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\xi_{i1}\xi_{i2}...\xi_{in}\xi_{jn}^{*}...\xi_{j2}^{*}\xi_{j1}^{*}>=\xi^{n}\frac{\delta^{2n}G(J^{*},J)}{\delta J_{i1}^{*}...\delta J_{in}^{*}\delta J_{j1}...\delta J_{jn}}\mid_{J=J^{*}=0}}
So now, we calculate by using of this theorem. In this case, we have four terms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Phi_{\alpha}^{*}(r,\tau),\sigma_{\alpha\beta}^{z}\Phi_{\beta}(r,\tau)\Phi_{\gamma}^{*}(r^{'},\tau^{'})\sigma_{\gamma\delta}^{z}\Phi_{\delta}(r^{'},\tau'))} inside the integral. If we make them in order we will have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\beta}(r,\tau)\Phi_{\delta}(r^{'},\tau')\Phi_{\gamma}^{*}(r^{'},\tau^{'})\Phi_{\alpha}^{*}(r,\tau)} we can get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}(G_{23}G_{14}-G_{13}G_{24})}
Where we used label 1,2,3,4 for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\beta}(r,\tau),\Phi_{\delta}(r^{'},\tau'),\Phi_{\gamma}^{*}(r^{'},\tau^{'}),\Phi_{\alpha}^{*}(r,\tau)} respectively. We can simplify more because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{23}\leftrightarrow G_{\delta\gamma}(r^{'}-r^{'},\tau^{'}-\tau^{'})} that means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma,\delta} should be the same and then we get zero for this term.
So
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}G_{\beta\gamma}(r-r^{'},\tau-\tau^{'})G_{\delta\alpha}(r-r^{'},\tau-\tau^{'})}
Then we calculate Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau e^{i\Omega_{n}\tau}\int d^{3}re^{-iq.r}\overline{D}(\tau,r)=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}\int_{0}^{\beta}d^{3}re^{-iq.r}\frac{1}{\beta}\sum_{i\omega_{n}}\frac{1}{V}\sum_{k}e^{-i\omega_{n}\tau}e^{ik.r}G_{\beta\gamma}(k,i\omega_{n})\frac{1}{\beta}\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i\nu_{n}}\frac{1}{V}\sum_{p}e^{i\nu_{n}\tau}e^{-ip.r}G_{\gamma\delta}(p,i\nu_{n})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}\delta_{\beta\gamma}\delta_{\gamma\delta}\frac{1}{\beta}\sum_{i\omega_{n}}\int\frac{d^{3}k}{(2\pi)^{3}}\frac{1}{i\omega_{n}-(\varepsilon_{k}-\mu)}\frac{1}{i\omega_{n}-i\Omega_{n}-(\varepsilon_{k-q}-\mu)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =2\int\frac{d^{3}k}{(2\pi)^{3}}(-\oint_{c}\frac{dz}{2\pi i}\frac{1}{z-(\varepsilon_{i}-\mu)}\frac{(\frac{1}{e^{\beta z}+1})}{z-i\Omega_{n}-(\varepsilon_{k-q}-\mu)})=2\int\frac{d^{3}k}{(2\pi)^{3}}\frac{n_{f}(\varepsilon_{k}-\mu)-n_{f}(\varepsilon_{k-q}-\mu)}{\varepsilon_{k}-\varepsilon_{k-q}-i\Omega_{n}}}
If we change we will get the real time Green's function.
For static limit we can simplify more by using this approximation
and for : that is Pauli paramagnetic response to the magnetic field.
So, as we saw in the previous part for an operator likeFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}[a_{\alpha1}(\tau_{1})a_{\alpha2}(\tau_{2})a_{\alpha2^{'}}^{+}(\tau_{2}^{'})a_{\alpha_{1}^{'}}^{+}(\tau_{1}^{'})]>_{0}}
we can write as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\Psi_{\alpha1}(\tau_{1})\Psi_{\alpha2}(\tau_{2})\Psi_{\alpha2^{'}}^{+}(\tau_{2}^{'})\Psi_{\alpha_{1}^{'}}^{+}(\tau_{1}^{'})]>_{0}=G_{\alpha1,\alpha2^{'}}(\tau_{2}-\tau_{2}^{'})G_{\alpha1,\alpha1^{'}}(\tau_{1}-\tau_{1}^{'})+\xi G_{\alpha2,\alpha1^{'}}(\tau_{2}-\tau_{1}^{'})G_{\alpha1,\alpha2^{'}}(\tau_{1}-\tau_{2}^{'})}
So only we need enumerate all the complete sets of contractions contributing to the thermal average of products of the potentioal V. It is convenient to represent this expansion in terms of diagrams. first consider the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\Psi^{*}(\tau),\Psi(\tau)]e^{-S}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=S_{0}+S_{int}} So we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\Psi^{*}(\tau),\Psi(\tau)]e^{-S_{0}}(1-S_{int}+\frac{1}{2!}S_{int}^{2}-...)}
Each outgoing line will be connected to an ingoing line with a directed line corresponding to the propagator.
First term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (S_{int})} gives us Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\int_{0}^{\beta}d\tau\sum_{\alpha\beta\gamma\delta}<\Psi_{\alpha}^{*}(\tau)\Psi_{\beta}^{*}\Psi_{\delta}(\tau)\Psi_{\gamma}(\tau)>_{0}}
The set of all possible ways of connecting interactions with propagators corresponds precisely to the set of all the contractions arising from Wick's theorem. So summation over a complete set of distinct diagrams will faithfully reproduce each of the desired contractions. At order n=1, there are two diagrams corresponding to the two contractions contributing to the integral.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\int_{0}^{\beta}d\tau\sum_{\gamma\delta}G_{\gamma}^{(0)}(0)G_{\delta}^{(0)}(0)V_{\gamma\delta\gamma\delta}=}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\xi\int_{0}^{\beta}d\tau\sum_{\gamma\delta}G_{\gamma}^{(0)}(0)G_{\delta}^{(0)}(0)V_{\delta\gamma\gamma\delta}=}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2!}\frac{1}{4}\frac{-1}{2}\int_{0}^{\beta}d\tau\int_{0}^{\beta}\sum_{\alpha\beta\gamma\delta}\sum_{\alpha^{'},\beta^{'},\gamma^{'},\delta^{'}}V_{\alpha^{'}\beta^{'}\gamma^{'}\delta^{'}}<\Psi_{\alpha}^{*}(\tau)\Psi_{\beta}^{*}(\tau)\Psi_{\delta}^{*}(\tau)\Psi_{\gamma}^{*}(\tau)\Psi_{\alpha^{'}}(\tau^{'})\Psi_{\beta^{'}}(\tau^{'})\Psi_{\delta^{'}}(\tau^{'})\Psi_{\gamma^{'}}(\tau^{'})>_{0}=}
 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +}
Fluctuation-Dissipation Theorem
In statistical mechanics people are mostly concerned with the evaluation of statistical averages of the various physical quantities; these averages represent, with a high degree of accuracy, the results expected from relevant measurements on the given system in equilibrium. Nevertheless, there do occur deviations from, or fluctuations about, these mean values. Though they are generally small, their study is of great physical interest for several reasons.
Firstly, it enables us to develop a mathematical scheme with the help of which the magnitude of the relevant fluctuations, under a variety of physical situations, can be estimated. Not surprisingly, we find that while in a single-phase system the fluctuations are thermodynamically negligible they can assume considerable importance in multi-phase systems, especially in the neighborhood of a critical point. In the latter case, we obtain a rather high degree of spatial correlation among the molecules of the system which, in turn, gives rise to phenomena such as critical opalescence.
Secondly, it provides a natural framework for understanding a class of phenomena that come under the heading "Brownian motion"; these phenomena relate properties such as the mobility of a fluid system, its coefficient of diffusion, etc. with temperature through the so-called Einstein relations. The mechanism of Brownian motion is vital in formulating, and in a certain sense answering, questions as to how "a given physical system, which is not in a state of equilibrium, finally approaches such a state" while "a physical system, which is already in a state of equilibrium, persists to stay in that state".
Thirdly, the study of fluctuations, as a function of time, leads to the concept of certain "correlation functions" that play a vital role in relating the dissipative properites of a system, such as the viscous resistance of a fluid or the electrical resistance of a conductor, with the microscopic properties of the system in a state of equilibrium; this relationship (between irreversible processes on one hand and equilibrium properties on the other) manifests itself in the so-called fluctuation-dissipation theorem. At the same time, a study of the "frequency spectrum" of fluctuations, which is related to the time-dependent correlation function through the fundamental theorem of Wiener and Khinchine, is of considerable value in assessing the "noise" met with in electrical circuits as well as in the transmission of electromagnetic signals.
Examples of fluctuation-dissipation theorem are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle E^2 \rangle - \langle E \rangle^2 = k_B T^2 C_V }
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle N^2 \rangle - \langle N \rangle^2 = \frac{\bar{N} k_B T \kappa_T}{v} }
whereby a fluctuation is related to an appropriate "susceptibility". In the case of energy fluctuations the relevant susceptibility is the specific heat at constant volume, and in the case of density fluctuations it is the thermal compressibility.
In general, the fluctuation-dissipation theorem relates a correlation function, or "fluctuation", to the imaginary part of a susceptibility, or "dissipation". We will now derive this relation. Let us begin with a real-time correlation function,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(t-t')=\langle \hat{O}(t)\hat{O}(t')\rangle=\frac{1}{Z}\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}(t)|m\rangle\langle m|\hat{O}(t')|n\rangle=\frac{1}{Z}\sum_{mn}e^{-\beta(E_n-\mu N)}e^{i(E_n-E_m)(t-t')/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
The Fourier transform of this function is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\omega)=\int_{-\infty}^{\infty}dt\,S(t)e^{i\omega t}=\frac{1}{Z}\int_{-\infty}^{\infty}dt\,\sum_{mn}e^{-\beta(E_n-\mu N)}e^{i(E_n-E_m+\hbar\omega)t/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{2\pi\hbar}{Z}\int_{-\infty}^{\infty}dt\,\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
Now we consider the response function,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(t-t')=-\frac{i}{\hbar}\theta(t-t')\langle [\hat{O}(t),\hat{O}(t')]\rangle=-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}e^{-\beta(E_n-\mu N)}[\langle n|\hat{O}(t)|m\rangle\langle m|\hat{O}(t')|n\rangle-\langle n|\hat{O}(t')|m\rangle\langle m|\hat{O}(t)|n\rangle]} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}e^{-\beta(E_n-\mu N)}[e^{i(E_n-E_m)(t-t')/\hbar}-e^{-i(E_n-E_m)(t-t')/\hbar}]\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle,}
or, exchanging Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} in the second term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(t-t')=-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]e^{i(E_n-E_m)(t-t')/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
We will now take the Fourier transform of this expression. Introducing a convergence factor, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(\omega)=\int_{-\infty}^{\infty}dt\,D^R(t)e^{i\omega t}=-\frac{i}{\hbar}\frac{1}{Z}\int_{0}^{\infty}dt\,\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]e^{i(E_n-E_m+\hbar\omega)t/\hbar}e^{-\hbar\eta t}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{\hbar}\frac{1}{Z}\sum_{mn}\frac{e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}}{E_m-E_n-\hbar(\omega+i\eta)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
If we take the imaginary part of this expression, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{1}{\hbar}\frac{1}{Z}\sum_{mn}\frac{\hbar\eta[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]}{(E_m-E_n-\hbar\omega)^2+\hbar^2\eta^2}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle,}
or, taking the limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\rightarrow 0} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{\pi}{Z}\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
We may replace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_m} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n+\hbar\omega} because of the delta function. If we do so, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{\pi}{Z}(1-e^{-\beta\hbar\omega})\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
If we compare this expression to the one we obtained for the correlation function, we find that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\omega)=-\frac{2\hbar}{1-e^{-\beta\hbar\omega}}\text{Im}\,D^R(\omega),}
which is the relation we sought.
The most striking feature of this theorem is that it relates, in a fundamental manner, the fluctuations of a physical quantity pertaining to the equilibrium state of the given system to a dissipative process which, in practice, is realized only when the system is subject to an external force that drives it away from equilibrium. Consequently, it enables us to determine the non-equilibrium properties of a given system on the basis of a knowledge of the thermal fluctuations occuring in the system when the system is in one of its equilibrium states!
Saddle point approximation and broken symmetry
Analytic Landscape
In analyzing problems in mathematical physics, one often finds it desirable to know the behavior of a function for large values of the variable or some parameter s, that is, the asymptotic behavior of the function. Specific examples are furnished by the gamma function and various Bessel functions. All these analytic functions are defined by integrals
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \int_{C}^{} F(z,s) dz } ......... (2.5.1)
where F is analytic in z and depends on a real parameter s. We write F(z) simply whenever possible.
Normally we evaluate such definite integrals of analytic functions along the real axis by deforming the path C to C' in the complex plane, so that |F| becomes small for all z on C'. This method succeeds as long as only isolated poles occur in the area between C and C'. The poles are taken into account by applying the residue theorem. The residues give a measure of the simple poles where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F| \rightarrow \infty } , which usually dominate and determine the value of the integral.
The behavior of such an integral in Eq. (2.5.1) clearly depends on the absolute value |F| of the integrand. Moreover, the contours of |F| often become more pronounced as s becomes large. Let us focus on a plot of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(x+iy)|^2 = U^2(x,y) + V^2(x,y) } , rather than the real part ReF = U and the imaginary part ImF = V separately. Such a plot of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F|^2 } over the complex plane is called the analytic landscape after Jensen who, in 1912, proved that it has only saddle points and troughs, but no peaks. Moreover, the troughs reach down all the way to the complex plane. In the absence of (simple) poles, saddle points are next in line to dominate the integral in Eq. (2.5.1). Hence the name saddle point method. At a saddle point the real part U of F has a local maximum, say, which implies that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial U}{\partial x} + \frac{\partial U}{\partial y} = 0 }
and therefore by the use of the Cauchy-Riemann conditions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial V}{\partial x} + \frac{\partial V}{\partial y} = 0 }
so that V has a minimum, or vice versa, and F'(z)=0. Jensen's theorem prevents U and V from having both a maximum or minimum. See the Figure below for a typical shape. We will choose the path C so that it runs over the saddle point and in the valleys elsewhere. If there are several saddle points, we treat each alike, and their contributions will add to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s \rightarrow \infty) } .
To prove that there are no peaks, assume there is one at zo. That is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(zo)|^2 > |F(z)|^2 } for all z in the neighborhood Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z-zo| \le r } . If
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z) = \sum_{n=0}^{\infty} a_n (z-zo)^n }
is the Taylor expansion at zo, the mean value m(F) on the circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = zo + r e^{i \phi} } becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m(F) = \frac{1}{2 \pi} \int_{0}^{2 \pi} |F(zo+r e^{i \phi})|^2 d \phi } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2 \pi} \int_{0}^{2 \pi} \sum_{m,n=0}^{\infty} a_{m}^{*} a_{n} r^{m+n} e^{i(n-m) \phi} d \phi } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{n=0}^{\infty} |a_n|^2 r^{2n} > |a_o|^2 = |F(zo)|^2} (2.5.2)
using orthogonality, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2 \pi} \int_{0}^{2 \pi} e^{i(n-m) \phi} d \phi = \delta_{n,m} } . Since m(F) is the mean value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F|^2 } on the circle of radius r, there must be a point z1 on it so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z1)|^2 > m(F) > |F(zo)|^2 } , which contradicts our assumption. Hence there can be no such peak.
Next, let us assume there is a minimum at zo so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < |F(z_0)|^2 < |F(z)|^2 } for all z in the neighborhood of zo. In other words, the dip in the valley does not go down to the complex plane. Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 > 0 } and, since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/F(z) } is analytic there, it has a Taylor expansion and zo would be a peak of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/|F(z)|^2 } , which is impossible. This proves Jensen's theorem. We now return to the integral in Eq. (2.5.1).
Saddle Point Method
Since each saddle point zo necessarily lies above the complex plane, that is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(zo)|^2 > 0 } , we write F in exponential form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{f(z,s)} } in its vicinity without loss of generality. At zo the tangential plane is horizontal, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\partial F / \partial z)|_{z=zo} = 0 } , or equivalently Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\partial f / \partial z)|_{z=zo} = 0 } . At zo, f has a power series
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = f(zo) + \frac{1}{2} f''(zo)(z-zo)^2 + ... } (2.5.3)
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = f(zo) + \frac{1}{2} (f''(zo) + \epsilon)(z-zo)^2 } (2.5.4)
upon collecting all higher powers in the (small) . Let us take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(zo) \neq 0 } for simplicity. Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(zo)(z-zo)^2 = - t^2 } (2.5.5)
for real t defines a line through zo (saddle point axis in the Figure). At zo, t=0. Along the axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Im[f''(zo)(z-zo)^2] } is zero and v = Imf(z) ~ Imf(zo) is constant if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } in Eq. (2.5.4) is neglected. Equation (2.5.5) can also be expressed in terms of angles,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-zo) = \frac{\pi}{2} - \frac{1}{2} arg f''(zo) = constant } (2.5.6)
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 = e^{2 Ref} } varies monotonically with Ref, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 \rightarrow e^{-t^2} } falls off exponentially from its maximum at t = 0 along this axis. Hence the name steepest decent. The line through zo defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(zo)(z-zo)^2 = + t^2 } (2.5.7)
is orthogonal to this axis (dot-dashed in the Figure), which is evident from its angle
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-zo) = - \frac{1}{2} arg f''(zo) = constant } (2.5.8)
when compared with Eq. (2.5.6). Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 } grows exponentially.
The curves Ref(z) = Ref(zo) go through zo so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Re[(f''(zo)+ \epsilon)(z-zo)^2] = 0 } , or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f''(zo)+ \epsilon)(z-zo)^2 = it } for real t. Expressing this in angles as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-zo) = \frac{\pi}{4} - \frac{1}{2} arg(f''(zo)+ \epsilon), t > 0 } (2.5.9a)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-zo) = - \frac{\pi}{4} - \frac{1}{2} arg(f''(zo)+ \epsilon), t < 0 } (2.5.9b)
and comparing with Eqs. (2.5.6) and (2.5.8) we note that these curves (dot-dashed in the Figure) divide the saddle point region into four sectors, two with Ref(z) > Ref(zo) (hence |F(z)| > |F(zo)|) shown shaded in the Figure, and two with Ref(z) < Ref(zo) (hence |F(z)| < |F(zo)|) . They are at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm (\pi / 4) } angles from the axis. Thus, the integration path has to avoid the shaded areas where |F| rises. Now we are ready to specialize the integrand F further in order to tie up the path selection with the asymptotic behavior as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s \rightarrow \infty } .
We assume that s appears linearly in the exponent, that is, we replace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{f(z,s)} \rightarrow e^{s f(z)} } . This dependence on s ensures that the saddle point at zo grows with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s \rightarrow \infty } , as is the case in most applications in physics. In order to account for the region far away from the saddle point that is not influenced by s, we include another analytic function g(z) that varies slowly near the saddle point and is independent of s. Altogether then our integral has the more appropriate and specific from
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \int_{C}^{} g(z) e^{s f(z)} dz } (2.5.10)
The path of the steepest decent is the saddle point axis when we neflect the higher order terms, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , in Eq. (2.5.4). With Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } , the path of the steepest decent is the curve close to the axis within the unshaded sectors, where v = Imf(z) is strictly constant, while Imf(z) is only approximately constant on the axis. We approximate I(s) by the integral along the piece of the axis inside the patch in the Figure, where (compare with Eq. (2.5.5)),
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = zo + x e^{i \alpha}, \alpha = \frac{\pi}{2} - \frac{1}{2} argf''(zo), a \le x \le b } (2.5.11)
We find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) \rightarrow e^{i \alpha} \int_{a}^{b} g(zo + x e^{i \alpha}) e^{s f(zo + x e^{i \alpha})} dx } (2.5.12a)
and the omitted part is small and can be estimated because Re[f(z)-f(zo)] has an upper negative bound, -R say, that depends on the size of the saddle point patch in the Figure (i.e., the values of a, b in Eq. (2.5.11)) that we choose. In Eq. (2.5.12) we use the power expansions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(zo + x e^{i \alpha}) = f(zo) + \frac{1}{2} f''(zo) e^{2i \alpha} x^2 + ... }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(zo + x e^{i \alpha}) = g(zo) + g'(zo) e^{i \alpha} x + ... } (2.5.12b)
and recall from Eq. (2.5.11) that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} f''(zo) e^{2i \alpha} = -\frac{1}{2} |f''(zo)| < 0 }
We find for the leading term
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = e^{i \alpha} g(zo) e^{s f(zo)} \int_{a}^{b} e^{-\frac{1}{2} s |f''(zo)| x^2} dx } (2.5.13)
As the integrand in Eq. (2.5.13) is essentially zero when x departs appreciably from the origin, we let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \rightarrow \infty } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \rightarrow -\infty } . The small error involved is straightforward to estimate. Noting that the remaining integral is just a Gauss error integral,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} e^{-\frac{1}{2} a^2 x^2} dx = \frac{\sqrt{2 \pi}}{a}}
we finally obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \frac{\sqrt{2 \pi} g(zo) e^{s f(zo)} e^{i \alpha}}{|s f''(zo)|^{1/2}} } (2.5.14)
where the phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } was introduced in Eq. (2.5.11).
Final Remark. We assumed that the only significant contribution to the integral came from the immediate vicinity of the saddle point(s) z = zo. This condition must be checked for each new problem.
Example. Asymptotic Form of the Factorial Function s!
In many physical problems, particularly in the field of statistical mechanics, it is desirable to have an accurate approximation of the gamma or factorial function of very large numbers. The factorial function may be defined by the Euler integral
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \int_{0}^{\infty} \rho^s e^{-\rho} d \rho = s^{s+1} \int_{0 C}^{\infty} e^{s(lnz - z)} dz } (2.5.15)
Here we have made the substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = zs } in order to throw the integral into the form required by Eq. (2.5.10). As before, we assume that s is real and positive, from which it follows that the integrand vanishes at the limits 0 and . By differentiating the z-dependence appearing in the exponent, we obtain
(2.5.16)
which shows that the point z = 1 is a saddle point. We let
(2.5.17)
with small x to describe the contour in the vicinity of the saddle point. Substituting into , we develop a series expansion
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = ln(1 + x e^{i \alpha}) - (1 + x e^{i \alpha}) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = x e^{i \alpha} - \frac{1}{2} x^2 e^{2i \alpha} + ... - 1 - x e^{i \alpha} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = - 1 - \frac{1}{2} x^2 e^{2i \alpha} } (2.5.18)
From this we see that the integrand takes on a maximum value (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-s} } ) at the saddle point if we choose our contour C to follow the real axis, a conclusion that we could have reached more or less intuitively.
Direct substitution into Eq. (2.5.14) with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = 0 } now gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \frac{\sqrt{2 \pi} s^{s+1} e^{-s}}{|s (-1^{-2})|^{1/2}} } (2.5.19)
Thus the first term in the asymptotic expansion of the factorial function is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \sqrt{2 \pi s} s^s e^{-s} } (2.5.20)
This result is the first term in Stirling's expansion of the factorial function. The method of steepest decent is probably the easiest way of obtaining this first term.
In the foregoing example the calculation was carried out by assuming s to be real. This assumption is not necessary. We may show that Eq. (2.5.19) also holds when s is replaced by the complex variable w, provided only that the real part of w is required to be large and positive.
Hubbard Model
The Hamiltonian of the Hubbard model is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -t \sum_{<rr'>}^{} \sum_{\sigma = \uparrow \downarrow} [C_{\sigma}^{+}(r) C_{\sigma}(r') + C_{\sigma}^{+}(r') C_{\sigma}(r)] + u \sum_{r}^{} C_{\uparrow}^{+}(r) C_{\uparrow}(r) C_{\downarrow}^{+}(r) C_{\downarrow}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -t \sum_{r, \sigma}^{} \sum_{\vec{\delta} = \hat{x}, \hat{y}}^{} [C_{\sigma}^{+}(r) C_{\sigma}(r+ \delta) + C_{\sigma}^{+}(r+ \delta) C_{\sigma}(r)] + u \sum_{r}^{} C_{\uparrow}^{+}(r) C_{\uparrow}(r) C_{\downarrow}^{+}(r) C_{\downarrow}(r)}
assuming that on average, there is only one particle per site.
Note that this Hamiltonian has global U(1) symmetry (charge conservation) :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}(r) \rightarrow e^{i \theta} C_{\sigma} (r) } ,
as well as global SU(2) symmetry (spin conservation):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma} \rightarrow u_{\alpha \beta} C_{\beta}(r) = (e^{i \vec{\theta} \cdot \vec{\sigma}})_{\alpha \beta} C_{\beta}(r) }
which is not obvious at this moment. To see this, let us re-express the second term in terms of spin operators: (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar = 1 } )
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(r) = \frac{1}{2} C_{\alpha}^{+}(r) \vec{\tau}_{\alpha \beta} C_{\beta}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}^2(r) = \frac{1}{4} C_{\alpha}^{+}(r) \tau_{\alpha \beta}^{a} C_{\beta}(r) C_{\gamma}^{+}(r) \tau_{\gamma \delta}^{a} C_{\delta}(r) }
Notice that any 2x2 matrix can be expressed in terms of Pauli matriies and unit matrix, that is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = \frac{1}{2} 1_{2x2} Tr[M] + \frac{1}{2} \sum_{a=1}^{3} \tau^a Tr[M \tau^a] }
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{ij} = \frac{1}{2} \delta_{ij} \delta_{kl} M_{lk} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a M_{kl} \tau_{lk}^a }
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M_{ij}}{\partial M_{\alpha \beta}} = \frac{1}{2} \delta_{ij} \delta_{kl} \frac{\partial M_{lk}}{\partial M_{\alpha \beta}} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a \tau_{lk}^a \frac{\partial M_{kl}}{\partial M_{\alpha \beta}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{i \alpha} \delta_{j \beta} = \delta_{ij} \delta_{kl} \delta_{l \alpha} \delta_{k \beta} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a \tau_{lk}^a \delta_{k \alpha} \delta_{l \beta} }
Therefore
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{a=1}^{3} \tau_{ij}^a \tau_{\beta \alpha}^a = 2 \delta_{i \alpha} \delta_{j \beta} - \delta_{ij} \delta_{\alpha \beta} }
or, relabeling the indicies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{a=1}^{3} \tau_{\alpha \beta}^a \tau_{\gamma \delta}^a = 2 \delta_{\alpha \delta} \delta_{\beta \gamma} - \delta_{\alpha \beta} \delta_{\delta \gamma} }
Now we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^2 = \frac{1}{4} \sum_{a=1}^3 \tau_{\alpha \beta}^{a} \tau_{\gamma \delta}^{a} C_{\alpha}^{+}(r) C_{\beta}(r) C_{\gamma}^{+}(r) C_{\delta}(r)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{4} (2 \delta_{\alpha \delta} \delta_{\beta \gamma} - \delta_{\alpha \beta} \delta_{\delta \gamma}) C_{\alpha}^{+}(r) C_{\beta}(r) C_{\gamma}^{+}(r) C_{\delta}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\alpha}^{+} C_{\beta} C_{\beta}^{+} C_{\alpha} - \frac{1}{4} C_{\alpha}^{+} C_{\alpha} C_{\beta}^{+} C_{\beta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} (C_{\uparrow} C_{\uparrow}^{+} + C_{\downarrow} C_{\downarrow}^{+}) C_{\uparrow} + \frac{1}{2} C_{\downarrow}^{+} (C_{\uparrow} C_{\uparrow}^{+} + C_{\downarrow} C_{\downarrow}^{+}) C_{\downarrow} - \frac{1}{4} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} + \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow} C_{\downarrow}^{+} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} C_{\uparrow} C_{\uparrow}^{+} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{4} (C_{\uparrow}^{+} C_{\uparrow} + 2 C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + C_{\downarrow}^{+} C_{\downarrow} )}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} + \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{4} C_{\uparrow}^{+} C_{\uparrow} - \frac{1}{4} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) - \frac{3}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} }
so
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} = - \frac{2}{3} S^2 + \frac{1}{2} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) }
The interaction part of the Hamiltonian now becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = - \frac{2}{3} u \sum_{r} \vec{S}(r) \cdot \vec{S}(r) + \frac{1}{2} u \sum_{r, \sigma} C_{\sigma}^{+}(r) C_{\sigma}(r) }
from which it is clear that H has SU(2) symmetry.
To write the coherent state path integral for the system, its Hamiltonian should be expressed in normal order
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S} \cdot \vec{S} = \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\beta} C_{\gamma}^{+} \vec{\tau}_{\gamma \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} ( [C_{\beta}, C_{\gamma}^{+}]_{-} - C_{\gamma}^{+} C_{\delta}) \vec{\tau}_{\gamma \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} \cdot \vec{\tau}_{\beta \delta} C_{\delta} - \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} C_{\alpha}^{+} C_{\alpha} - \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} }
Hence
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = ( - \frac{u}{2} + \frac{u}{2} ) \sum_{r, \sigma} C_{\sigma}^{+}(r) C_{\sigma}(r) -\frac{2}{3} u \sum_{r} (- \frac{1}{4}) C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} = \frac{1}{6} \sum_{r} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta}}
Now the path integral for the system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int D[\psi_{\sigma}^{*}, \psi_{\sigma}] e^{- \int_{0}^{\beta} \sum_{r} L } }
where the Lagrangian is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = \psi_{\sigma}^{*}(r, \tau) (\frac{\partial}{\partial \tau} - \mu) \psi_{\sigma}(r, \tau) - t \sum_{\delta} [ \psi_{\sigma}^{*}(r, \tau) \psi_{\sigma}(r+ \delta, \tau) + \psi_{\sigma}^{*}(r + \delta, \tau) \psi_{\sigma}(r, \tau) ] - \frac{u}{6} [ \psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) ]^2 }
To deal with the quartic interaction term, we use the Hubbard-Stratonovic transformation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ \frac{u}{6} [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)]^2 d \tau } = const \cdot \int d \phi_x d \phi_y d \phi_z e^{- \frac{1}{2} \vec{\phi} \cdot \vec{\phi} d \tau} e^{\lambda \vec{\phi} \cdot [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)] d \tau } }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\eta} = \psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) } , then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \frac{1}{2} \vec{\phi} \cdot \vec{\phi} d \tau + \lambda \vec{\phi} \cdot \vec{\eta} d \tau = - \frac{1}{2} (\vec{\phi} - \lambda \vec{\eta})^2 d \tau + \frac{1}{2} \lambda^2 \vec{\eta}^2 d \tau }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = - \sqrt{u/3} } . Hence
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ \frac{u}{6} [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)]^2 d \tau } = const \cdot ( \int d \phi_x d \phi_y d \phi_z e^{- \frac{1}{2} \vec{\phi}^2 d \tau} ) e^{\frac{\lambda^2}{2} \vec{\eta}^2 d \tau} }
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{int} = \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \psi_{\alpha}^{*} \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) + \frac{1}{2} [\vec{\phi}(r, \tau)]^2 }
Now the partition function of the system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = const \cdot \int D[\phi] \int D[\psi_{\alpha}^{*}, \psi_{\alpha}] e^{- \int_{0}^{\beta} d \tau \sum_{r} (L_o + L_{int})} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = const \cdot \int D[\phi] e^{- \int_{0}^{\beta} d \tau \sum_{r} \frac{1}{2} [\vec{\phi}(r, \tau)]^2} \cdot Det[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{\alpha \beta} + \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \vec{\tau}_{\alpha \beta} ]}
Furthermore, define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{- \frac{1}{2} \int_{\tau} \sum_{r} \phi^2} e^{ln Det[...]} = e^{- S_{eff}[\vec{\phi}]} }
Applying the saddle-point approximation we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 = \frac{\delta S_{eff}(\vec{\phi})}{\delta \phi_{\alpha}(r, \tau)} = - \phi_{\alpha}^{(s)}(r, \tau) + \frac{\delta}{\delta \phi_{\alpha (r, \tau)}} Tr[ln[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{\alpha \beta} + \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \vec{\tau}_{\alpha \beta}]] }
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha}^{(s)}(r, \tau) = Tr [[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{ij} + \sqrt{\frac{u}{3}} \phi^{(s)}(r', \tau') \cdot \vec{\tau}_{ij}]_{\alpha \beta}^{-1} \sqrt{\frac{u}{3}} \tau_{\alpha \beta}^a \delta(r-r') \delta(\tau - \tau')] }
Mean Field Theory and its relation to the Saddle Point Approximation
We may relate the above calculation of the saddle point for the path integral to the concept of broken symmetry. Before we do so, however, we will introduce mean field theory, which, as it will turn out, is related to the saddle point approximation. Our discussion of mean field theory will follow that found in Fradkin's book (E. Fradkin, Field Theories of Condensed Matter Physics, Westview Press (1998)), though some of our definitions differ from his. We will illustrate the basic idea of mean field theory using the Hubbard model written in terms of the spin operator, which we repeat here.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{2}{3}U\sum_{\vec{r}}\vec{S}(\vec{r})\cdot\vec{S}(\vec{r})}
Throughout this section, we will be working in two dimensions, and at zero temperature.
The mean field approximation we will use is as follows. We first rewrite the spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r})} in the Hamiltonian as a sum of its expectation value plus its deviation from said expectation value (the fluctuation term),
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r})=\langle\vec{S}(\vec{r})\rangle+[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle],}
obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{2}{3}U\sum_{\vec{r}}\langle\vec{S}(\vec{r})\rangle\cdot\langle\vec{S}(\vec{r})\rangle-\tfrac{4}{3}U\sum_{\vec{r}}\langle\vec{S}(\vec{r})\rangle\cdot[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle]-\tfrac{2}{3}U\sum_{\vec{r}}[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle]\cdot[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle].}
Finally, we drop the last term, which is quadratic in the fluctuations, thus obtaining the mean field Hamiltonian,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{4}{3}U\sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{S}(\vec{r})+\tfrac{2}{3}U\sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{M}(\vec{r}),}
where we define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\langle\vec{S}(\vec{r})\rangle.}
From this point on, we will treat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} as a parameter. Note that this Hamiltonian, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} is not zero, breaks the SU(2) symmetry of the original Hubbard model due to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})\cdot\vec{S}(\vec{r})} term.
We will now rewrite this Hamiltonian in momentum space. If we introduce the Fourier transform of the creation and annihilation operators,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{r})=\frac{1}{\sqrt{N}}\sum_{\vec{k}}c_{\sigma}(\vec{k})e^{i\vec{k}\cdot\vec{r}},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} is the number of sites, then the non-interacting part of the Hamiltonian will be diagonalized:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=-2t(\cos{k_x a}+\cos{k_y a}).}
We will assume that these operators are periodic, in that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k})} is the same as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k}+\vec{G})} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{G}} is a reciprocal lattice vector.
If we perform a similar transformation on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\frac{1}{N}\sum_{\vec{k}}\vec{M}(\vec{k})e^{i\vec{k}\cdot\vec{r}},}
and similarly for the spin operator, we get, for the interaction part of the Hamiltonian,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{S}(\vec{r})=\frac{1}{N^2}\sum_{\vec{k}\vec{k}'}\sum_{\vec{r}}\vec{M}(\vec{k}')\cdot\vec{S}(\vec{k})e^{i(\vec{k}+\vec{k}')\cdot\vec{r}}=\frac{1}{N}\sum_{\vec{k}}\vec{M}(\vec{-k})\cdot\vec{S}(\vec{k})=\frac{1}{N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{S}(\vec{k})}
In the last step, we used the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} is real. Similarly,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{M}(\vec{r})=\frac{1}{N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{M}(\vec{k}).}
We will also want to know Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{k})} in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k}).}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{k})=\sum_{\vec{r}}\vec{S}(\vec{r})e^{-i\vec{k}\cdot\vec{r}}=\tfrac{1}{2}\sum_{\vec{r},\alpha\beta}c_{\alpha}^{\dagger}(\vec{r})\tau_{\alpha\beta}c_{\beta}(\vec{r})e^{-i\vec{k}\cdot\vec{r}}=\frac{1}{2N}\sum_{\vec{k}'\vec{k}'',\alpha\beta}\sum_{\vec{r}}c_{\alpha}^{\dagger}(\vec{k}')\tau_{\alpha\beta}c_{\beta}(\vec{k}'')e^{i(\vec{k}''-\vec{k}'-\vec{k})\cdot\vec{r}}=\tfrac{1}{2}\sum_{\vec{k}',\alpha\beta}c_{\alpha}^{\dagger}(\vec{k}')\tau_{\alpha\beta}c_{\beta}(\vec{k}+\vec{k}')}
Putting everything together, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})+\tfrac{1}{2}U\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\frac{2U}{3N}\sum_{\vec{k}\vec{k}',\alpha\beta}\vec{M}^{\ast}(\vec{k})\cdot c_{\alpha}^{\dagger}(\vec{k}')\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{k}')+\frac{2U}{3N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{M}(\vec{k}).}
Let us now assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} has a specific form, namely
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\vec{M}_0\cos(\vec{Q}\cdot\vec{r}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{Q}=\left (\tfrac{\pi}{a},\tfrac{\pi}{a}\right ),}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\tfrac{1}{2}\vec{M}_0(e^{i\vec{Q}\cdot\vec{r}}+e^{-i\vec{Q}\cdot\vec{r}}).}
This would correspond to an antiferromagnetic ordering. The only two non-zero Fourier components of this vector are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{Q})=\vec{M}(-\vec{Q})=\tfrac{1}{2}N\vec{M}_0,}
so that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})+\tfrac{1}{2}U\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}-\vec{Q})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
From this point forward, we will work at half-filling. That is, we will introduce a chemical potential term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mu\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k}),}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\tfrac{1}{2}U,} so that the second term is canceled out. It can be shown that, at half-filling, the Hubbard model becomes antiferromagnetic in two dimensions, as we are assuming here. The Hamiltonian is now just
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}-\vec{Q})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We will now diagonalize this Hamiltonian. To do so, we will make use of the periodicity of the lattice to reduce the third term to the Hermitian adjoint of the second. We note that the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{Q}} is exactly half of a reciprocal lattice vector. Therefore, if we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\vec{Q}} to all wave vectors in the third term, it becomes the Hermitian adjoint of the second:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k}+\vec{Q})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We may split the first term into two terms, each over half of the Brillouin zone. We may do the same for the next two terms as well. If we use the "nesting" property,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k}+\vec{Q})=-2t[\cos(k_x a+\pi)+\cos(k_y a+\pi)]=2t(\cos{k_x a}+\cos{k_y a})=-\epsilon(\vec{k}),}
we may rewrite the above as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}={\sum_{\vec{k},\sigma}}'\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-{\sum_{\vec{k},\sigma}}'\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k}+\vec{Q})c_{\sigma}(\vec{k}+\vec{Q})-\tfrac{2}{3}U{\sum_{\vec{k},\alpha\beta}}'\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{2}{3}U{\sum_{\vec{k},\alpha\beta}}'\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k}+\vec{Q})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2,}
where a prime on a sum means that the wave vectors are only summed over the upper half (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_y>0} ) of the Brillouin zone.
To diagonalize this Hamiltonian, we will write it in matrix form. Each term in the sum can be written in the form,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{\dagger}(\vec{k})\mathcal{H}(\vec{k})\Psi(\vec{k}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\vec{k})=\left [\begin{array}{c} c_{\uparrow}(\vec{k}) \\ c_{\downarrow}(\vec{k}) \\ c_{\uparrow}(\vec{k}+\vec{Q}) \\ c_{\downarrow}(\vec{k}+\vec{Q}) \end{array}\right ]}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})=\left [\begin{array}{cc} \epsilon(\vec{k}) & -\tfrac{2}{3}U\vec{M}_0\cdot\vec{\tau} \\ -\tfrac{2}{3}U\vec{M}_0\cdot\vec{\tau} & -\epsilon(\vec{k}) \end{array}\right ],}
where each entry represents a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 2} block. If we square the above matrix, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathcal{H}(\vec{k})]^2=\left [\begin{array}{cc} [\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2 & 0 \\ 0 & [\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2 \end{array}\right ].}
We therefore see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})} possesses two eigenvalues, given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\pm}(\vec{k})=\pm\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}.}
The spectrum therefore has a gap, with magnitude Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{4}{3}U|\vec{M}_0|.}
We may see that these represent states of definite projection of spin along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} . Let us suppose that we chose to quantize the spin of our electrons along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} , or, equivalently, we chose our coordinates so that, say, the z-axis was along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} . Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})} becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})=\left [\begin{array}{cccc} \epsilon(\vec{k}) & 0 & -\tfrac{2}{3}UM_0 & 0 \\ 0 & \epsilon(\vec{k}) & 0 & \tfrac{2}{3}UM_0 \\ -\tfrac{2}{3}UM_0 & 0 & -\epsilon(\vec{k}) & 0 \\ 0 & \tfrac{2}{3}UM_0 & 0 & -\epsilon(\vec{k}) \\ \end{array}\right ].}
This matrix can easily be reduced to block diagonal form, and it only mixes operators that create particles with the same spin (that is, it only mixes a spin up state with another spin up state, for example). We also find that the above energies, in fact, form doubly degenerate pairs, each corresponding to a spin up or a spin down state. We may then obtain the result for any relative orientation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} to the spin quantization axis via the appropriate SU(2) transformation applied to each pair of operators in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\vec{k})} at the same wave vector.
Now that we know the energies, we may now write down the energy of the ground state of our system. The ground state is simply the state in which all of the negative energy single-particle states are occupied. It also has zero average spin because we occupy an equal number of spin up and spin down states. Its energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{GS}=-2{\sum_{\vec{k}}}'E_{+}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2=-2{\sum_{\vec{k}}}'\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We will now need to minimize this energy with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0.} We are essentially applying the variational principle, using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} as a parameter. We require that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=\frac{\partial E_{GS}}{\partial M_{0,i}}=-2{\sum_{\vec{k}}}'\frac{\tfrac{4}{9}U^2 M_{0,i}}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}+\tfrac{2}{3}NUM_{0,i}.}
Rearranging the above equation, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sum_{\vec{k}}}'\frac{M_{0,i}}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}M_{0,i}.}
There are two possible solutions. One of these is to simply set all of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{0,i}=0,} which corresponds to a paramagnetic state. The other is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sum_{\vec{k}}}'\frac{1}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}.}
Notice that the above equation only involves the magnitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0.} This means that the direction may be chosen arbitrarily.
Let us now take the thermodynamic limit. In this case, the sum on the left-hand side becomes an integral:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Na^2 \int_{-\pi/a}^{\pi/a}\frac{dk_x}{2\pi}\int_{0}^{\pi/a}\frac{dk_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}.}
If we change variables to the dimensionless quantities, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \kappa_{i}=k_{i}a} , we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\pi}^{\pi}\frac{d\kappa_x}{2\pi}\int_{0}^{\pi}\frac{d\kappa_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{\kappa})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{U}.}
Using the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon(-\kappa_x,\kappa_y)=\epsilon(\kappa_x,\kappa_y),} we may write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\pi}\frac{d\kappa_x}{2\pi}\int_{0}^{\pi}\frac{d\kappa_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{\kappa})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{2U}.}
Having derived the mean field equations, let us now relate this method to the saddle point approximation given above. We consider the final result of the last section,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{a}^{(s)}(\vec{r}, \tau)=Tr\left [\left [\left (\frac{\partial}{\partial \tau} - \mu + \hat{h}_o\right ) + \sqrt{\frac{U}{3}} \phi^{(s)}(\vec{r}', \tau') \cdot \vec{\tau}\right ]_{\alpha \beta}^{-1}\delta(\vec{r}-\vec{r}')\delta(\tau - \tau')\sqrt{\frac{U}{3}}\tau_{\beta\alpha}^a\right ].}
We note that the factor,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [\left (\frac{\partial}{\partial \tau} - \mu + \hat{h}_o\right ) + \sqrt{\frac{U}{3}} \phi^{(s)}(\vec{r}', \tau') \cdot \vec{\tau}\right ]_{\alpha\beta}^{-1}\delta(\vec{r}-\vec{r}')\delta(\tau-\tau'),}
is just the Green's function for a generalized form of our mean field Hamiltonian (minus the term depending only on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} ) at equal positions and equal times. Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{a}^{(s)}(\vec{r}, \tau)=Tr\left [G(\vec{r},\tau;\vec{r},\tau)\sqrt{\frac{U}{3}}\tau^a\right ].}
It is shown, for example, by Fetter and Walecka (A. Fetter and J. D. Walecka, Quantum Theory of Many-Body Systems, McGraw-Hill, New York (1971)), that the above is simply proportional to the average of the spin at a given point:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\sqrt{\frac{4U}{3}}\langle \vec{S}(\vec{r},\tau)\rangle}
If we take
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\sqrt{\frac{4U}{3}}\vec{M}(\vec{r})}
and assume that it has the form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\vec{\phi}_0\cos(\vec{Q}\cdot\vec{r})} , then we will have reduced the problem to the one that we considered above.
A few comments on mean field theory are in order. First of all, it is only reliable at weak coupling; that is, in our case, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\ll t} . This is because the approximation we make involves dropping a term of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} ; if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} is too large, then this approximation is questionable. Second of all, this method introduces a bias into our analysis. We assume that the system has a certain order; in this case, we assumed that it was antiferromagnetic. We would require a separate analysis to ensure that the system does, in fact, have the order that we assume. To illustrate these problems, we consider the Hubbard model in one dimension. It has been solved exactly, and it turns out that no ordering tendencies of any kind are present. However, if we perform a mean field analysis much like the one above, we would predict that the system is antiferromagnetic.
With these issues in mind, let us now solve the mean field equation and obtain a value for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} . We note that the most dominant contributions will come from the region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=0} , especially if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} is small; these regions are those for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x+k_y=\pi} . In fact, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|=0,} then there will be a logarithmic singularity along this line. We will take advantage of this fact to find an approximate solution. We may use the trigonometric identity,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos{\kappa_x}+\cos{\kappa_y}=2\cos\left (\frac{\kappa_x+\kappa_y}{2}\right )\cos\left (\frac{\kappa_x-\kappa_y}{2}\right ),}
to rewrite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=-4t\cos\left (\frac{\kappa_x+\kappa_y}{2}\right )\cos\left (\frac{\kappa_x-\kappa_y}{2}\right ).}
We now expand the first factor about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x+k_y=\pi} and drop the second factor (that is, we assume it is approximately 1; given that the first factor is small, it should not make much difference), obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})\approx 2t(\kappa_x+\kappa_y-\pi).}
We will also perform the following transformation on the variables of integration:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\frac{\kappa_x+\kappa_y-\pi}{2},\,\kappa=\kappa_x-\kappa_y}
This transformation has a Jacobian of 1. We will approximate the new region of integration with a rectangle with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\kappa|<\pi} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |K|<\tfrac{\Lambda}{2}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is an appropriate cutoff. Since the integrand will be constant with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa} , the integral just gives a constant coefficient. With all of these approximations, the mean field equation becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\Lambda/2}^{\Lambda/2}\frac{dK}{2\pi}\,\frac{1}{\sqrt{16t^2K^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{2U},}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\Lambda/2}^{\Lambda/2}\frac{dK}{2\pi}\,\frac{1}{\sqrt{K^2+\tfrac{1}{36}\left (\tfrac{U}{t}\right )^2|\vec{M}_0|^2}}=\frac{6t}{U}.}
We now use the fact that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dx\,\frac{1}{\sqrt{x^2+a^2}}=\sinh^{-1}\left (\frac{x}{a}\right )+C}
to obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\pi}\sinh^{-1}\left (\frac{t}{U}\frac{18\Lambda}{|\vec{M}_0|}\right )=\frac{6t}{U}.}
Solving for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} , we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|=\frac{18t}{U}\frac{\Lambda}{\sinh(6\pi t/U)}.}
If we assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\ll t} , which is necessary for mean field theory to be valid anyway, we may approximate this as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|\approx \frac{36t}{U}\Lambda e^{-6\pi t/U}.}
We see that, as long as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{U}{t}} is small, then so is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} . We also note that we get a non-zero solution for any value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} . In the exact solution, however, we do not get antiferromagnetic order for arbitrary Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} .
Individual Wiki Projects
Lattice Gas Model of Liquid Helium
Double-layer Quantum Hall Ferromagnets
scaling theory of localization
Renormalization Group (RG) Approach to Interacting Fermions
Effective field theory and RG approach to interacting Fermions
Bose-Einstein Condensation in Spin-gaped Systems
Random Phase Approximation for the Collective Modes of Nuclei
Bethe Ansatz for Many-Particle Systems
Charge Density Wave (CDW) Quantum Phase Transition in Hubbard Model in Zero Temperature
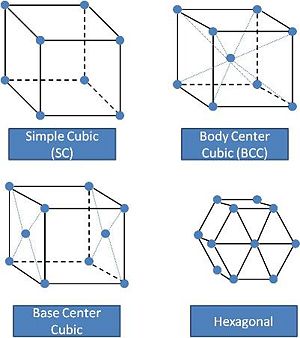
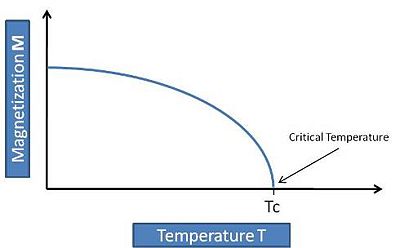
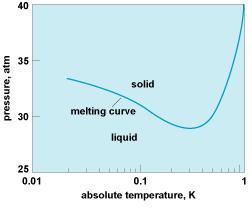
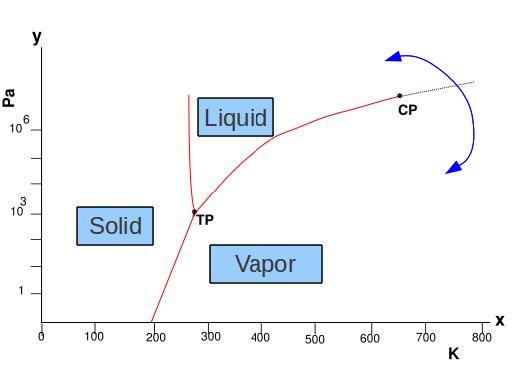
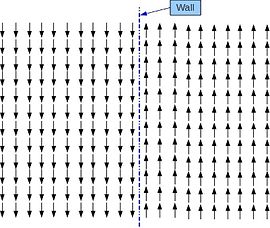
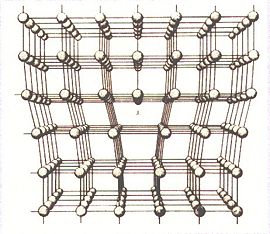

![{\displaystyle 0=\int d\mathbf {x} [{\frac {\delta ^{2}F}{\delta j_{\beta }(\mathbf {x} )\delta _{\gamma }(\mathbf {y} )}}j_{\gamma }(\mathbf {x} )-{\frac {\delta ^{2}F}{\delta j_{\gamma }(\mathbf {x} )\delta j_{\gamma }(\mathbf {y} )}}j_{\beta }(\mathbf {x} )+{\frac {\delta F}{j_{\beta }(\mathbf {x} )}}\delta (\mathbf {x-y} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eef1641d6d5fb5dbda8cedb4992c7b50c4a1c4f)
![{\displaystyle =\int d\mathbf {x} [G_{\beta \gamma }(\mathbf {x-y} )j_{\gamma }(\mathbf {x} )-G_{\gamma \gamma }(\mathbf {x-y} )j_{\beta }(\mathbf {x} )+\phi _{\beta }(\mathbf {x} )\delta (\mathbf {x-y} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44a9d9e32492e217b9de725b4f5c0986f9340ca2)





































![{\displaystyle \left[a_{i},a_{j}^{+}\right]=\delta _{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6702d33360f07a594c960df04a5e8de721fd534)






![{\displaystyle S^{z}|m\rangle =(S-{\hat {n}})|m\rangle =[S-(S-m)]|m\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85e1ca55bd37ca9f520963a3a76a24a8a8483c2)































![{\displaystyle \left[\alpha _{k_{1}},\alpha _{k_{2}}^{+}\right]=\delta _{k_{1}k_{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6609f1dd15c74e950b97b506fbf3577d41b6bc0)
























































![{\displaystyle {\frac {\partial S}{\partial t}}=\int d^{3}{\vec {r}}\ \left[-\overbrace {\left(j_{\epsilon }-hj_{m_{z}}+X'h_{\theta }\right)} ^{=j_{Q}}\cdot {\frac {\nabla T}{T^{2}}}-{\frac {1}{T}}\left(j_{m_{z}}\cdot \nabla h+h_{\theta }\cdot \nabla h-X'\nabla \cdot h_{\theta }\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b95c708e9fe962fc95b7d0b738e9443260b114)




































































































































![{\displaystyle e^{A}e^{B}=e^{B}e^{A}e^{[A,B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bbf69d37071d26172a5526e637ed18b535d04cd)




![{\displaystyle [a_{\alpha ,}\left|\phi \right\rangle \left\langle \phi \right|]=a_{\alpha }\left|\phi \right\rangle \left\langle \phi \right|-\left|\phi \right\rangle \left\langle \phi \right|a_{\alpha }=(\phi _{\alpha }-{\frac {\partial }{\partial \phi _{\alpha }^{*}}})\left|\phi \right\rangle \left\langle \phi \right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/767faf8146da485d3c54ed91b8deacdc8fb7220c)
![{\displaystyle [a_{\alpha ,}\int {\underset {\alpha '}{\prod }}{\frac {d\phi _{\alpha '}^{*}d\phi _{\alpha '}}{2\pi i}}e^{-{\underset {\alpha '}{\sum }}\phi _{\alpha '}^{*}\phi {}_{\alpha '}}\left|\phi \right\rangle \left\langle \phi \right|]=\int {\underset {\alpha '}{\prod }}{\frac {d\phi _{\alpha '}^{*}d\phi _{\alpha '}}{2\pi i}}e^{-{\underset {\alpha '}{\sum }}\phi _{\alpha '}^{*}\phi {}_{\alpha '}}(\phi _{\alpha }-{\frac {\partial }{\partial \phi _{\alpha }^{*}}})\left|\phi \right\rangle \left\langle \phi \right|=\int {\underset {\alpha '}{\prod }}{\frac {d\phi _{\alpha '}^{*}d\phi _{\alpha '}}{2\pi i}}(\phi _{\alpha }+{\frac {\partial }{\partial \phi _{\alpha }^{*}}})e^{-{\underset {\alpha '}{\sum }}\phi _{\alpha '}^{*}\phi {}_{\alpha '}}\left|\phi \right\rangle \left\langle \phi \right|=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/584aaa8ae5273cf8a7cd6464fd44c5d4cadb8d97)



![{\displaystyle \left\langle 0\right|l.h.s\left|0\right\rangle =\int {\underset {\alpha }{\prod }}{\frac {d\phi _{\alpha }^{*}d\phi _{\alpha }}{2\pi i}}e^{-{\underset {\alpha }{\sum }}\phi _{\alpha }^{*}\phi {}_{\alpha }}\left\langle 0|\phi \right\rangle \left\langle \phi |0\right\rangle =\int {\underset {\alpha }{\prod }}{\frac {d(Re\phi _{\alpha })d(Im\phi _{\alpha })}{\pi }}e^{-{\underset {\alpha }{\sum }}[(Re\phi {}_{\alpha })^{2}+(Im\phi {}_{\alpha })^{2}]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acdd813d8d680321eca65be006d1feaacf218827)


































![{\displaystyle \int _{-\infty }^{\infty }{\frac {dx_{1}...dx_{n}}{(2\pi )^{n/2}}}e^{-{\frac {1}{2}}x_{i}A_{ij}x_{j}+x_{i}J_{j}}=[DetA]^{-1/2}e^{{\frac {1}{2}}J_{i}A_{ij}^{-1}J_{j}}..........(GI1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/420bcb2ce86c2cc03fcd18a6c76f839bee542159)

![{\displaystyle \int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}{\frac {dx_{j}^{*}dx_{j}}{2\pi i}}e^{-x_{i}^{*}H_{ij}x_{j}+J_{i}^{*}x_{i}+J_{i}x_{i}^{*}}=[DetH]^{-1}e^{J_{i}^{*}H_{ij}^{-1}J_{j}}..........(GI2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d1fdce7f09739d514757cb8c1f178348f1afc68)
![{\displaystyle \int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}d\eta _{j}^{*}d\eta _{j}e^{-\eta _{i}^{*}H_{ij}\eta _{j}+\xi _{i}^{*}\eta _{i}+\xi _{i}\eta _{i}^{*}}=[DetH]e^{\xi _{i}^{*}H_{ij}^{-1}\xi _{j}}..........(GI3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/febe043e3f0f69e67c034cdf56c306c827881323)








![{\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }{\frac {dx_{1}...dx_{n}}{(2\pi )^{n/2}}}e^{-{\frac {1}{2}}x_{i}A_{ij}x_{j}+x_{i}J_{j}}&=\int _{-\infty }^{\infty }{\frac {dy_{1}...dy_{n}}{(2\pi )^{n/2}}}e^{-{\frac {1}{2}}y_{i}A_{ij}y_{j}+{\frac {1}{2}}J_{a}A_{ab}^{-1}J_{b}}\\&=\int _{-\infty }^{\infty }{\frac {dz_{1}...dz_{n}}{(2\pi )^{n/2}}}e^{-{\frac {1}{2}}a_{1}z_{1}^{2}-{\frac {1}{2}}a_{2}z_{2}^{2}...-{\frac {1}{2}}a_{n}z_{n}^{2}+{\frac {1}{2}}J_{a}A_{ab}^{-1}J_{b}}\\&={\frac {1}{(2\pi )^{n/2}}}\int _{-\infty }^{\infty }dz_{1}e^{-{\frac {1}{2}}a_{1}z_{1}^{2}}\int _{-\infty }^{\infty }dz_{2}e^{-{\frac {1}{2}}a_{2}z_{2}^{2}}...\int _{-\infty }^{\infty }dz_{n}e^{-{\frac {1}{2}}a_{n}z_{n}^{2}}e^{{\frac {1}{2}}J_{a}A_{ab}^{-1}J_{b}}\\&={\frac {1}{(2\pi )^{n/2}}}{\sqrt {\frac {2\pi }{a_{1}}}}...{\sqrt {\frac {2\pi }{a_{n}}}}e^{{\frac {1}{2}}J_{i}A_{ij}^{-1}J_{j}}\\&={\frac {1}{\sqrt {a_{1}a_{2}...a_{n}}}}e^{{\frac {1}{2}}J_{i}A_{ij}^{-1}J_{j}}\\&=[DetA]^{-1/2}e^{{\frac {1}{2}}J_{i}A_{ij}^{-1}J_{j}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1037e7b3fde90b51f5b8077ce3548dd132589cbb)


![{\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}{\frac {dx_{j}^{*}dx_{j}}{2\pi i}}e^{-x_{i}^{*}H_{ij}x_{j}+J_{i}^{*}x_{i}+J_{i}x_{i}^{*}}&=\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}{\frac {dy_{j}^{*}dy_{j}}{2\pi i}}e^{-y_{i}^{*}H_{ij}y_{j}+J_{a}^{*}H_{ab}^{-1}J_{b}}\\&=\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}{\frac {dz_{j}^{*}dz_{j}}{2\pi i}}e^{-a_{1}z_{1}^{*}z_{1}-a_{2}z_{2}^{*}z_{2}...-a_{n}z_{n}^{*}z_{n}+J_{a}^{*}H_{ab}^{-1}J_{b}}\\&=\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}\left\{{\frac {dRez_{j}dImz_{j}}{\pi }}e^{-a_{j}[(Rez_{j})^{2}+(Imz_{j})^{2}]}\right\}e^{J_{a}^{*}H_{ab}^{-1}J_{b}}\\&={\underset {j=1}{\prod }}^{n}\left\{\int _{-\infty }^{\infty }{\frac {dRez_{j}}{\sqrt {\pi }}}e^{-a_{j}(Rez_{j})^{2}}\right\}\left\{\int _{-\infty }^{\infty }{\frac {dImz_{j}}{\sqrt {\pi }}}e^{-a_{j}(Imz_{j})^{2}}\right\}e^{J_{a}^{*}H_{ab}^{-1}J_{b}}\\&={\frac {1}{a_{1}a_{2}...a_{n}}}e^{J_{i}^{*}H_{ij}^{-1}J_{j}}\\&=[DetH]^{-1}e^{J_{i}^{*}H_{ij}^{-1}J_{j}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/603f3ccbeb8ae65d7cf4f0c9c259a5592b7c7c4a)











![{\displaystyle J=[DetM]^{-1}=\left|{\frac {\partial (\eta ^{*},\eta )}{\partial (\xi ^{*},\xi )}}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f33d09d4d48f4516cd847a19f36dca458a17170)




![{\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}d\eta _{j}^{*}d\eta _{j}e^{-\eta _{i}^{*}H_{ij}\eta _{j}+\xi _{i}^{*}\eta _{i}+\xi _{i}\eta _{i}^{*}}&=\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}d\rho _{j}^{*}d\rho _{j}e^{-\rho _{i}^{*}H_{ij}\rho _{j}}e^{\xi _{a}^{*}H_{ab}^{-1}\xi _{b}}\\&=\int _{-\infty }^{\infty }{\underset {j=1}{\prod }}^{n}d\chi _{j}^{*}d\chi _{j}e^{-\sum _{j}h_{j}\chi _{j}^{*}\chi _{j}}e^{\xi _{a}^{*}H_{ab}^{-1}\xi _{b}}\\&=({\underset {j=1}{\prod }}^{n}h_{j})e^{\xi _{a}^{*}H_{ab}^{-1}\xi _{b}}\\&=[DetH]e^{\xi _{i}^{*}H_{ij}^{-1}\xi _{j}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6f8e472402b14025c875fd7d16c329c48cc1cd)



![{\displaystyle T_{\tau }[O_{\alpha _{1}}^{(\tau _{1})}O_{\alpha _{2}}^{(\tau _{2})}....O_{\alpha _{n}}^{(\tau _{n})}]=\xi ^{p}O_{\alpha _{p1}}(\tau _{p1})O_{\alpha _{p2}}(\tau _{p2})....O_{\alpha _{pn}}(\tau _{pn})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e85ec533858f10fbdb7aae57891083473c18906c)
![{\displaystyle T_{\tau }[a_{\alpha }^{(H)}(\tau )a_{\beta }^{(H)^{+}}(\tau ^{'})]=a_{\alpha }^{(H)^{+}}(\tau )a_{\beta }^{(H)}(\tau ^{'})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da70da53ef5afe5cbd55bc0c39481d687f4676fd)