Angular Momentum as a Generator of Rotations in 3D

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian ${\mathcal {H}}$, it describes how a state $|\Psi \rangle$ evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Let us consider an infinitesimal rotation described by a vector $\mathbf {\alpha } \!$ directed along the axis about which the rotation takes place and whose magnitude is the angle of the rotation. We then have

$\mathbf {r} '=\mathbf {r} +\mathbf {\alpha } \times \mathbf {r} =\mathbf {r} +\delta \mathbf {r} ,$

where $\delta \mathbf {r} =\mathbf {\alpha } \times \mathbf {r}$ is the change in the position vector $\mathbf {r} \!$ of the particle due to such a rotation.

Let us now consider a function of position, $\psi (\mathbf {r} ).$ Substituting in the rotated coordinate and expanding to first order in $\delta \mathbf {r} ,$ we obtain

$\psi \left(\mathbf {r} +\mathbf {\delta } \mathbf {r} \right)=\left[1+\mathbf {\alpha } \cdot \left(\mathbf {r} \times \mathbf {\nabla } \right)\right]\psi \left(\mathbf {r} \right)$

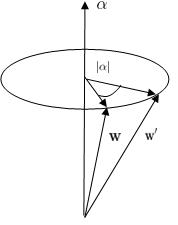
Figure 1: Illustration of the rotation considered here.

The expression,

$1+\mathbf {\alpha } \cdot (\mathbf {r} \times \mathbf {\nabla } ),$

may therefore be interpreted as an operator that performs an infinitesimally small rotation of position coordinates. Noticing that

$\mathbf {r} \times \mathbf {\nabla } ={\frac {i}{\hbar }}{\hat {\mathbf {L} }},$

we may write this infinitesimal rotation operator as

${\hat {R}}_{inf}=1+{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}.$

Note that this expression only applies to infinitesimal rotations. We may construct a rotation operator for finite rotations, however, as follows. Let $\mathbf {\alpha }$ be a finite rotation. Let us imagine performing this rotation as a sequence of $N\!$ rotations by ${\frac {\mathbf {\alpha } }{N}},$ where $N\!$ is large. Each of these rotations may be treated as infinitesimal. The full rotation operator becomes

${\hat {R}}(\mathbf {\alpha } )=\left(1+{\frac {i}{\hbar }}{\frac {\mathbf {\alpha } }{N}}\cdot {\hat {\mathbf {L} }}\right)^{N}.$

If we now let $N\rightarrow \infty ,$ we obtain

${\hat {R}}(\mathbf {\alpha } )=e^{i\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}/\hbar }.$

In this form, we recognize that angular momentum is a generator of rotations, similarly to how linear momentum generates translations.

The transformation rule for an operator is thus

${\hat {O}}'=e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}}{\hat {O}}e^{-{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}}.$

This expression is valid for any rotation. We see that, if the operator commutes with both position and momentum, then it will remain unchanged by a rotation.

We can also calculate the effect of the unitary operator $e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}}$ on the wave function, as follows. We first determine the effect of the operator on a position eigenstate:

$\langle \mathbf {r} _{0}|e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}}\mathbf {\hat {\mathbf {r} }} e^{-{\frac {i}{\hbar }}\mathbf {\alpha } \cdot {\hat {\mathbf {L} }}}=\langle \mathbf {r} _{0}|{\hat {\mathbf {r} }}'=\mathbf {r} '_{0}\langle \mathbf {r} _{0}|$

As expected, the effect is to produce another position eigenstate, this one at the image of the rotation. The effect on the wavefunction is therefore as follows.

$\psi '(\mathbf {r} _{0})=\langle \mathbf {r} _{0}|\psi '\rangle =\langle \mathbf {r} _{0}|e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }|\psi \rangle =\langle \mathbf {r} '_{0}|\psi \rangle =\psi (\mathbf {r} '_{0})$

This is just the wave function evaluated at the rotated point.