Harmonic Oscillator Spectrum and Eigenstates: Difference between revisions
No edit summary |
|||
| Line 11: | Line 11: | ||
The Hamiltonian of the one-dimensional harmonic oscillator is: | The Hamiltonian of the one-dimensional harmonic oscillator is: | ||
<math>H=\frac{p^2}{2m}+\ | <math>H=\frac{p^2}{2m}+\tfrac{1}{2}kx^2,</math> | ||
or, in terms of the natural frequency, <math>\omega=\sqrt{\frac{k}{m}},</math> | or, in terms of the natural frequency, <math>\omega=\sqrt{\frac{k}{m}},</math> | ||
<math>H=\frac{p^2}{2m}+\ | <math>H=\frac{p^2}{2m}+\tfrac{1}{2}m\omega^2 x^2.</math> | ||
With the aid of the operator identity, | With the aid of the operator identity, | ||
| Line 24: | Line 24: | ||
<math> | <math> | ||
H=\hbar\omega\left( | H=\hbar\omega\left (\frac{m\omega}{2\hbar}x^2+\frac{p^2}{2m\hbar\omega}\right )=\hbar\omega\left (\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}}\right )\left (\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}\right )+\tfrac{1}{2}\hbar\omega | ||
</math> | </math> | ||
If we now define the operators, | |||
<math>\hat{a}=\sqrt{\frac{m\omega}{2\hbar}}x+ | <math>\hat{a}=\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}</math> | ||
and | |||
<math>\hat{a}^{\dagger}=\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}},</math> | |||
we may write the Hamiltonian as | |||
<math>H=\hbar\omega\left(\hat{a}^{\dagger}\hat{a}+\frac{1}{2}\right ).</math> | |||
One may easily show that the operators <math>\hat{a}\!</math> and <math>\hat{a}^{\dagger}</math> satisfy the commutation relation, <math>[\hat{a},\hat{a}^{\dagger}]=1.</math> | |||
Let us now define <math>\hat{n}=\hat{a}^{\dagger}\hat{a}.</math> Note that any eigenstate of <math>\hat{n}</math> is also an eigenstate of the Hamiltonian. let us denote the normalized eigenstates of <math>\hat{n}</math> as <math>|n\rangle,</math> which are defined such that <math>\hat{n}|n\rangle=n|n\rangle.</math> One may verify that the eigenvalues <math>n\!</math> must be positive using the Schwartz inequality. | |||
Now, let's see how <math>\hat{a}\!</math> and <math>\hat{a}^{\dagger}\!</math> act on an energy eigenstate <math>|\Psi\rangle\!</math>: | Now, let's see how <math>\hat{a}\!</math> and <math>\hat{a}^{\dagger}\!</math> act on an energy eigenstate <math>|\Psi\rangle\!</math>: | ||
| Line 78: | Line 81: | ||
It is remarkable that the ground state energy of a quantum oscillator is not zero, instead it is <math>\frac{1}{2}\hbar\omega </math>. This significant feature is important in modern physics, such as quantum fluctuation and vacuum energy. | It is remarkable that the ground state energy of a quantum oscillator is not zero, instead it is <math>\frac{1}{2}\hbar\omega </math>. This significant feature is important in modern physics, such as quantum fluctuation and vacuum energy. | ||
==Excited state wave function== | ==Excited state wave function== | ||
Revision as of 14:08, 8 August 2013
The one-dimensional harmonic oscillator consists of a particle moving under the influence of a harmonic oscillator potential, which has the form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=\frac{1}{2}k x^2,} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is the "spring constant".
We see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)\rightarrow \infty} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow \pm\infty.} Therefore, all stationary states of this system are bound, and thus the energy spectrum is discrete and non-degenerate. Furthermore, because the potential is an even function, the parity operator commutes with Hamiltonian, and thus the wave functions will be either even or odd.
The energy spectrum and the energy eigenstates can be found by either the algebraic method using raising and lowering operators, which is described below, or by the analytic method described in the next section.
Solution of the Harmonic Oscillator by Operator Methods
The Hamiltonian of the one-dimensional harmonic oscillator is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\frac{p^2}{2m}+\tfrac{1}{2}kx^2,}
or, in terms of the natural frequency, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=\sqrt{\frac{k}{m}},}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\frac{p^2}{2m}+\tfrac{1}{2}m\omega^2 x^2.}
With the aid of the operator identity,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^2+B^2=(A-iB)(A+iB)-i[A,B],\!}
we may factorize the Hamiltonian as follows.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\hbar\omega\left (\frac{m\omega}{2\hbar}x^2+\frac{p^2}{2m\hbar\omega}\right )=\hbar\omega\left (\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}}\right )\left (\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}\right )+\tfrac{1}{2}\hbar\omega }
If we now define the operators,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}=\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}=\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}},}
we may write the Hamiltonian as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\hbar\omega\left(\hat{a}^{\dagger}\hat{a}+\frac{1}{2}\right ).}
One may easily show that the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}} satisfy the commutation relation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{a},\hat{a}^{\dagger}]=1.}
Let us now define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}=\hat{a}^{\dagger}\hat{a}.} Note that any eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} is also an eigenstate of the Hamiltonian. let us denote the normalized eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle,} which are defined such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}|n\rangle=n|n\rangle.} One may verify that the eigenvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} must be positive using the Schwartz inequality.
Now, let's see how Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}\!} act on an energy eigenstate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle\!} : For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\hat{a} |\Psi\rangle = \left(E-\hbar\omega\right)|\Psi\rangle }
This means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a} |\Psi\rangle} is also an energy eigenstate but corresponding to a lower energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E-\hbar\omega\!} . Therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} is called the lowering operator.
Similarly,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\hat{a}^{\dagger}|\Psi\rangle = \left(E+\hbar\omega\right)|\Psi\rangle }
and so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}\!} is called the raising operator.
So, starting from any energy eigenstates, we can construct all other energy eigenstates by applying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}\!} repeatedly. Although there is no limit to the number of times we can apply Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}\!} , there is a limit to the number of times we can apply Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} . The process of lowering energy must stop at some point, since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E>0} . For the eigenstate of lowest energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi_0\rangle} (the ground state), we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}|\Psi_0\rangle=0\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \left( \sqrt{\frac{m\omega}{2\hbar}}x+\sqrt{\frac{\hbar}{2m\omega}}\frac{d}{dx}\right) \Psi_0(x)=0\!}
This is a first order ordinary differential equation, which can be easily solved, and the result is as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_0(x)=A e^{-\frac{m\omega}{2\hbar}x^2}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\!} is a constant, which can be determined from the normalization condition:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\int_{-\infty}^{\infty}|\Psi_0(x)|^2 dx = \int_{-\infty}^{\infty}dx A^2 e^{-\frac{m\omega}{\hbar}x^2}= A^2\sqrt{\frac{\pi\hbar}{m\omega}}\Rightarrow A=\left(\frac{m\omega}{\pi\hbar}\right)^{\frac{1}{4}}}
Thus, normalized ground state wave function is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_0(x)=\left(\frac{m\omega}{\pi\hbar}\right)^{\frac{1}{4}}e^{-\frac{m\omega}{2\hbar}x^2}}
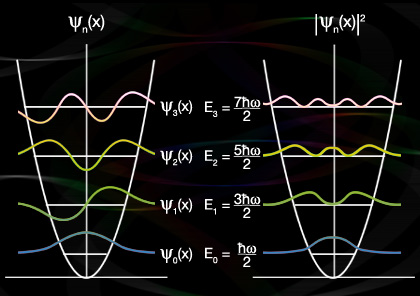
The energy spectrum of 1-D harmonic oscillator is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ {E}_{n}=\hbar\omega\left(n+\frac{1}{2}\right); n=0,1,2,\ldots}
It is remarkable that the ground state energy of a quantum oscillator is not zero, instead it is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\hbar\omega } . This significant feature is important in modern physics, such as quantum fluctuation and vacuum energy.
Excited state wave function
Energy eigenstates with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E>0\!} are called excited states. By applying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}} repeatedly and after normalization process we obtain the wave function for excited states as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi_n\rangle=\frac{(\hat{a}^{\dagger})^n}{\sqrt{n!}}|\Psi_0\rangle\!}
In the position representation
where is the Hermite polynomial.
In the momentum representation the solution looks similar. The raising and lowering operators are defined:
The ground state is found by requiring the lowering operator acting on a state to annihilate it:
We obtain the ground state by solving the differential equation and normalizing it:
Applying the raising operator repeatedly to this ground state and applying the correct additional normalization factor produces all of the excited states. In terms of the Hermite polynomials these are:
Note the appearance of the imaginary unit which is not present in the position representation of these states. This solution can also be obtained by performing Fourier transformation upon the result in position representation, since momentum and position are conjugate variables.
Notice that there are two parts in the wave function of excited states: the Gaussian function part and the Hermite polynomial part. The former accounts for the behavior of the wave function at long distances, while the later accounts for the behavior of the wave function at short distance and the number of nodes of the wave function.
The Quantum Harmonic Oscillator is of particular interest as a problem due to the fact that similar equations show up for many different applications. For example, the QHO appears when considering atomic vibrations, quantum LC circuits, and phonon modes in solids.
Problems on Harmonic oscillator
A nice problem concerning proof of the Virial Theorem in the case of the QHO