Harmonic Oscillator Spectrum and Eigenstates

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

The one-dimensional harmonic oscillator consists of a particle moving under the influence of a harmonic oscillator potential, which has the form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=\frac{1}{2}k x^2,} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is the "spring constant".

We see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)\rightarrow \infty} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow \pm\infty.} Therefore, all stationary states of this system are bound, and thus the energy spectrum is discrete and non-degenerate. Furthermore, because the potential is an even function, the parity operator commutes with Hamiltonian, and thus the wave functions will be either even or odd.

The energy spectrum and the energy eigenstates can be found by either the algebraic method using raising and lowering operators, which is described below, or by the analytic method described in the next section.

Solution of the Harmonic Oscillator by Operator Methods

The Hamiltonian of the one-dimensional harmonic oscillator is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\frac{p^2}{2m}+\tfrac{1}{2}kx^2,}

or, in terms of the natural frequency, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=\sqrt{\frac{k}{m}},}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\frac{p^2}{2m}+\tfrac{1}{2}m\omega^2 x^2.}

With the aid of the operator identity,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^2+B^2=(A-iB)(A+iB)-i[A,B],\!}

we may factorize the Hamiltonian as follows.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\hbar\omega\left (\frac{m\omega}{2\hbar}x^2+\frac{p^2}{2m\hbar\omega}\right )=\hbar\omega\left (\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}}\right )\left (\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}\right )+\tfrac{1}{2}\hbar\omega }

If we now define the operators,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}=\sqrt{\frac{m\omega}{2\hbar}}x+i\frac{p}{\sqrt{2m\hbar\omega}}}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}=\sqrt{\frac{m\omega}{2\hbar}}x-i\frac{p}{\sqrt{2m\hbar\omega}},}

we may write the Hamiltonian as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\hbar\omega\left(\hat{a}^{\dagger}\hat{a}+\frac{1}{2}\right ).}

One may easily show that the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}} satisfy the commutation relation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{a},\hat{a}^{\dagger}]=1.}

Let us now define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}=\hat{a}^{\dagger}\hat{a},} and denote the normalized eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle,} which are defined such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}|n\rangle=n|n\rangle.} Note that any eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} is also an eigenstate of the Hamiltonian, with eigenvalue

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n=\left (n+\tfrac{1}{2}\right )\hbar\omega.}

One may verify that the eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\geq 0\!} by acting on the left of this definition with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|.} There is therefore a lower bound of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}\hbar\omega} on the energy of any state of the harmonic oscillator. This "zero-point energy" is a remarkable and significant feature peculiar to quantum mechanics. One may view this as a consequence of the Heisenberg uncertainty principle; because it is impossible to perfectly localize a particle in both position and momentum spaces, a particle in a harmonic oscillator potential will always possess a non-zero energy relative to the minimum of the potential.

We may now determine what the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}} do to the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}.} Acting to the left on the definition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}|n\rangle=n|n\rangle,} with each of these operators and employing the above commutation relation, we may show that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}|n\rangle=\sqrt{n}|n-1\rangle}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle.}

We have thus shown that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}} is a "lowering operator", in the sense that, when applied to the eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n,\!} we obtain a result that is proportional to the eigenstate with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n-1.\!} For a similar reason, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}^{\dagger}} is a "raising operator".

We may use the above results to further restrict the possible values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n.\!} We may show that it is quantized, and can only take non-negative integer values; i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0,\,1,\,2,\,\ldots} Let us suppose that an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} with a positive non-integer eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} exists. Without loss of generality, let us suppose that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<n<1,\!} since one can generate such a state from any other such eigenstate by repeated application of the lowering operator. If we act on this state with the lowering operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}} , then we will generate an eigenstate with a negative eigenvalue (note that the factor, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{n},} does not vanish in this case!), which cannot exist, as pointed out earlier.

The only way to guarantee that no states with negative values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} are generated is to restrict Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} to be a non-negative integer. This is guaranteed because, by repeated application of the lowering operator, we will eventually obtain the state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}|0\rangle=0.} Therefore, we have shown that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle} is the ground state of the harmonic oscillator.

So, starting from any energy eigenstate, we can construct all other energy eigenstates by applying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}\!} or ${\hat {a}}^{\dagger }\!$ repeatedly. In particular, by repeated application of the raising operator, we may generate all of the eigenstates of the harmonic oscillator from its ground state:

$|n\rangle ={\frac {({\hat {a}}^{\dagger })^{n}}{\sqrt {n!}}}|0\rangle$

The Ground State Wave Function

We may use the above results to easily determine the ground state of the harmonic oscillator in position space. Starting from the fact that ${\hat {a}}|0\rangle =0,\!$ we may write, remembering that $p\rightarrow -i\hbar {\frac {d}{dx}}$ in the position basis,

$\left({\sqrt {\frac {m\omega }{2\hbar }}}x+{\sqrt {\frac {\hbar }{2m\omega }}}{\frac {d}{dx}}\right)\psi _{0}(x)=0\!$

This is a first order ordinary differential equation, which can be easily solved, and the result is

$\psi _{0}(x)=Ae^{-m\omega x^{2}/2\hbar },$

where $A\!$ is a normalization constant. Upon normalization, we find that the ground state wave function is

$\psi _{0}(x)=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{-m\omega x^{2}/2\hbar }.$

We may obtain the ground state wave function in momentum space as well. Remembering that, in this case, $x\rightarrow i\hbar {\frac {d}{dp}},$ the differential equation satisfied by the momentum-space wave function is

$\phi _{0}(p)={\frac {1}{(m\omega \pi \hbar )^{1/4}}}e^{-p^{2}/2m\omega \hbar }$

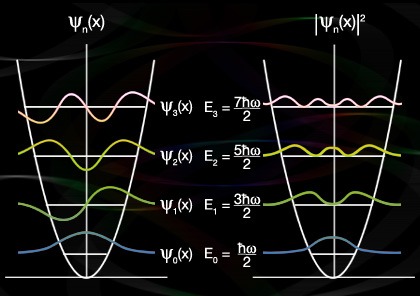
Excited state wave function

Illustration of the harmonic oscillator potential along with its eigenstates and its energy spectrum.

Energy eigenstates with $E>0\!$ are called excited states. By applying $a^{\dagger }$ repeatedly and after normalization process we obtain the wave function for excited states as follows:

$|\Psi _{n}\rangle ={\frac {({\hat {a}}^{\dagger })^{n}}{\sqrt {n!}}}|\Psi _{0}\rangle \!$

In the position representation

$\langle x|\Psi _{n}\rangle =\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}{\frac {1}{\sqrt {2^{n}n!}}}H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)e^{-{\frac {m\omega }{2\hbar }}x^{2}}\!$

where $H_{n}(\xi )=(-1)^{n}e^{\xi ^{2}}{\frac {d^{n}}{d\xi ^{n}}}e^{-\xi ^{2}}$ is the Hermite polynomial.

In the momentum representation the solution looks similar. The raising and lowering operators are defined:

${\hat {a}}^{\dagger }=i{\sqrt {\frac {m\omega \hbar }{2}}}{\frac {d}{dp}}-{\frac {ip}{\sqrt {2m\omega \hbar }}}$

${\hat {a}}=i{\sqrt {\frac {m\omega \hbar }{2}}}{\frac {d}{dp}}+{\frac {ip}{\sqrt {2m\omega \hbar }}}$

Applying the raising operator repeatedly to this ground state and applying the correct additional normalization factor produces all of the excited states. In terms of the Hermite polynomials these are:

$\Psi _{n}(p)={\frac {(-i)^{n}}{\sqrt {2^{n}n!}}}\left({\frac {1}{\pi m\omega \hbar }}\right)^{\frac {1}{4}}H_{n}\left({\frac {p}{\sqrt {m\omega \hbar }}}\right)e^{\frac {-p^{2}}{2m\omega \hbar }}$

Note the appearance of the imaginary unit $i$ which is not present in the position representation of these states. This solution can also be obtained by performing Fourier transformation upon the result in position representation, since momentum and position are conjugate variables.

Notice that there are two parts in the wave function of excited states: the Gaussian function part and the Hermite polynomial part. The former accounts for the behavior of the wave function at long distances, while the later accounts for the behavior of the wave function at short distance and the number of nodes of the wave function.

The Quantum Harmonic Oscillator is of particular interest as a problem due to the fact that similar equations show up for many different applications. For example, the QHO appears when considering atomic vibrations, quantum LC circuits, and phonon modes in solids.

Problems on Harmonic oscillator

Problem 1

Problem 2

A nice problem concerning proof of the Virial Theorem in the case of the QHO

External Link

More details about the normalization process can be found in Griffiths, Introduction to Quantum Mechanics, 2nd Ed. pg 47