Coulomb Potential Scattering: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
No edit summary
 
(3 intermediate revisions by the same user not shown)
Line 9: Line 9:
==Scattering From a Yukawa Potential in the Born Approximation==
==Scattering From a Yukawa Potential in the Born Approximation==


[[Image:Yukawa_Gaussian_Exp.jpg|thumb|400px|left|'''Comparison the differential cross sections for various potential type'''<br/>Here we compare the differential cross sections for the Yukawa, Gaussian and exponential potential. We can see that for small <math> q\alpha \!</math> all differential cross sections are similar. The differential cross section of the exponential potential decreases faster than the others and that of the Yukawa potential decreases little bit slower than the others.]]
[[Image:Yukawa_Gaussian_Exp.jpg|thumb|400px|left|'''Comparison the differential cross sections for various potential type'''<br/>Here we compare the differential cross sections for the Yukawa, Gaussian and exponential potential. We can see that for small <math> q\alpha \!</math> all differential cross sections are similar. The differential cross section of the exponential potential decreases faster than the others and that of the Yukawa potential decreases more slowly than the others.]]
 
As alluded to earlier, let us first consider the Yukawa potential,


Let's look at an example of a Screened Coulomb (Yukawa) Potential, where we have a potential:
<math>V(r)=V_0\frac{e^{-\alpha r}}{r}.</math>
<math>V(r)=V_0\frac{e^{-\alpha r}}{r}.</math>


The scattering amplitude can be written by:
Within the Born approximation, the scattering amplitude is
:<math>
 
<math>
\begin{align}
\begin{align}
f &= -\frac{m}{2\pi\hbar^2}\int_0^\infty dr' r'^2 2\pi\frac{e^{-i|\mathbf{k}'-\mathbf{k}|r'}-e^{i|\mathbf{k}-\mathbf{k}'|r'}}{-i|\mathbf{k}'-\mathbf{k}|r'}\frac{V_0e^{-\alpha r'}}{r'} \\
f(\theta) &= -\frac{m}{2\pi\hbar^2}2\pi\int_0^\infty dr'\,r'^2 \frac{e^{-i|\mathbf{k}'-\mathbf{k}|r'}-e^{i|\mathbf{k}-\mathbf{k}'|r'}}{-i|\mathbf{k}'-\mathbf{k}|r'}\frac{V_0e^{-\alpha r'}}{r'} \\
&= -\frac{2mV_0}{\hbar^2}\int_0^\infty dr' r'^2 \frac{\sin\left(|\mathbf{k}'-\mathbf{k}|r'\right)}{|\mathbf{k}'-\mathbf{k}|r'}\frac{e^{-\alpha r'}}{r'} \\
&= -\frac{2mV_0}{\hbar^2}\int_0^\infty dr' r'^2 \frac{\sin\left(|\mathbf{k}'-\mathbf{k}|r'\right)}{|\mathbf{k}'-\mathbf{k}|r'}\frac{e^{-\alpha r'}}{r'} \\
&= -\frac{2mV_0}{\hbar^2}\frac{1}{\left(\left|\mathbf{k}'-\mathbf{k}\right|\right)^2+\alpha^2}  
&= -\frac{2mV_0}{\hbar^2}\frac{1}{\left(\left|\mathbf{k}'-\mathbf{k}\right|\right)^2+\alpha^2}  
Line 23: Line 25:
</math>
</math>


For the elastic scattering <math> \left| \mathbf{k} \right| = \left| \mathbf{k'} \right| = k \!</math>. Therefore,  
For the elastic scattering <math> \left| \mathbf{k} \right| = \left| \mathbf{k'} \right| = k \!</math>. Therefore,
:<math>
<math>
(\left|\mathbf{k}'-\mathbf{k}\right|)^2 = 2k\sin\frac{\theta}{2}
(\left|\mathbf{k}'-\mathbf{k}\right|)^2 = 2k\sin\frac{\theta}{2}
</math>
</math>


Thus, we have
and thus
:<math>
 
f = -\frac{2mV_0}{\hbar^2}\frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}
<math>
f = -\frac{2mV_0}{\hbar^2}\frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}.
</math>
</math>


The differential cross section is then


thus we have the differential cross section:
<math>\frac{d\sigma}{d\Omega}= \left( \frac{2mV_0}{\hbar^2} \right) ^2 \left( \frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}\right)^2.</math>
:<math>\frac{d\sigma}{d\Omega}= \left( \frac{2mV_0}{\hbar^2} \right) ^2 \left( \frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}\right) ^2</math>


==Exact Coulomb Scattering Cross Section==
==Exact Coulomb Scattering Cross Section==
[[Image:ParabolicCoordinates.png|thumb|400px|left|'''Parabolic coordinates'''<br/><math>\phi\!</math> represents rotation about the z-axis, <math>\xi\!</math> represents the parabolas with their vertex at a minimum, and <math>\eta\!</math> represents parabolas with their vertex at a maximum.]]
[[Image:ParabolicCoordinates.png|thumb|400px|left|'''Parabolic coordinates'''<br/><math>\phi\!</math> represents rotation about the z-axis, <math>\xi\!</math> represents the parabolas with their vertices at a minimum, and <math>\eta\!</math> represents parabolas with their vertices at a maximum.]]


When we are considering scattering due to the Coulomb potential, we can not neglect the effect of this potential at large distances because it is only a <math>\frac{1}{r}</math> potential.  
When we are considering scattering due to the Coulomb potential, we can not neglect the effect of this potential at large distances because it is only a <math>\frac{1}{r}</math> potential.  


Use a change of coordinates from Cartesian to parabolic coordinates:
We will work in parabolic coordinates, which are related to Cartesian coordinates by
:<math>\xi=\sqrt{x^2+y^2+z^2}-z</math>
 
:<math>\eta=\sqrt{x^2+y^2+z^2}+z</math>
<math>\xi=\sqrt{x^2+y^2+z^2}-z</math>
:<math>\phi=\tan^{-1}(\frac{y}{x})</math>
 
<math>\eta=\sqrt{x^2+y^2+z^2}+z</math>
 
<math>\phi=\tan^{-1}\left (\frac{y}{x}\right )</math>
 
The [[Schrödinger Equation|Schrödinger equation]] in parabolic coordinates is


<math> \left[ - \frac{\hbar^2}{2\mu}\frac{4}{\xi+\eta} \left( \frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{\xi+\eta}{4\xi\eta}\frac{\partial^2}{\partial \phi^2} \right) -\frac{2Ze^2}{\xi+\eta} \right] \psi=\frac{\hbar^2k^2}{2\mu}\psi.</math>


So now we can write the [[Schrödinger equation]] in parabolic coordinates:
Recall that, for a spherically symmetric potential, the scattering amplitude is a function of <math>\theta\!</math> only; therefore, we will seek solutions that are independent of <math>\phi.\!</math>
:<math> \left[ - \frac{\hbar^2}{2\mu}\frac{4}{\xi+\eta} \left( \frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{\xi+\eta}{4\xi\eta}\frac{\partial^2}{\partial \phi^2} \right) -\frac{2Ze^2}{\xi+\eta} \right] \psi=\frac{\hbar^2k^2}{2\mu}\psi</math>


So we will seek solutions which are independent of <math>\phi\!</math>. Recall that the scattering amplitude is a function of <math>\theta\!</math> only.
We will look for solution of the form,


Look for solution of the form:
<math>\psi(\xi,\eta,\phi)=e^{\frac{i}{2}k(\eta-\xi)}\Phi(\xi)=e^{ikz}\Phi(r-z).</math>


:<math>\psi=e^{\frac{i}{2}k(\eta-\xi)}\Phi(\xi)=e^{ikz}\Phi(r-z)</math>
The [[Schrödinger Equation|Schrödinger equation]] then becomes


Then the equation becomes:
<math> \left[ \xi\frac{\partial^2}{\partial \xi^2}+(1-ik\xi)\frac{\partial}{\partial \xi}+\frac{Ze^2\mu}{k\hbar^2}k \right]\Phi(\xi)=0.</math>
:<math> \left[ \xi\frac{\partial^2}{\partial \xi^2}+(1-ik\xi)\frac{\partial}{\partial \xi}+\frac{Ze^2\mu}{k\hbar^2}k \right]\Phi(\xi)=0</math>


We can tidy up the notation a little bit by using the following substitution:
We now assume a series solution,
:<math>\lambda=\frac{Ze^2\mu}{k\hbar^2}</math>


Now let:
<math>\Phi(\xi)=\sum_{n=0}^\infty a_n \xi^n.</math>
:<math>\Phi(\xi)=\sum_{n=0}^\infty a_n \xi^n</math>


From this we can write:
The recursion relation for the coefficients is then
:<math>\frac{a_{n+1}}{a_{n}}=\frac{in-\lambda}{(n+1)^2}k=\frac{n+i\lambda}{(n+1)^2}ik</math>


<math>\frac{a_{n+1}}{a_{n}}=\frac{in-\lambda}{(n+1)^2}k=\frac{n+i\lambda}{(n+1)^2}ik,</math>


Recall the confluent hypergeometric function:
where
:<math>_1F_1(a,c,z)=1+\frac{a}{c}z+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\dots+\frac{a(a+1)\dots(a+n-1)}{c(c+1)\dots(c+n-1)}\frac{z^n}{n!}+\dots</math>


We can then write the recursion formula as the following:
<math>\lambda=\frac{Ze^2\mu}{k\hbar^2}.</math>
:<math>\dfrac{\alpha_{n+1}}{\alpha_n}= \left( \dfrac{a+n}{c+n} \right) \dfrac{1}{n+1}</math>


This implies that:
Recall that the confluent hypergeometric function <math>{}_1F_1</math> is given by
:<math>\Phi(\xi)=A_1F_1(i\lambda,1,ik\xi)\!</math>
where the confluent geometric function is written in terms of three new variables, and <math>A_1\!</math> is a c-number.


Now we can write the wavefunction due to Coulomb scattering:
<math>_1F_1(a,c,z)=1+\frac{a}{c}z+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\dots+\frac{a(a+1)\dots(a+n-1)}{c(c+1)\dots(c+n-1)}\frac{z^n}{n!}+\dots</math>
:<math>\psi(r,z)=A_1F_1(i\lambda,1,ik(r-z))e^{ikz}\!</math>


Now we should look at the limit where z is taken to go to infinity, and our confluent hypergeometric function is rewritten as:
The recursion formula for its coefficients is
:<math>_1F_1(a,c,z)=\frac{\Gamma(c)(-z)^a}{\Gamma(c-a)} \left[ 1-\frac{a(a-c+1)}{z} \right] +\frac{\Gamma(c)}{\Gamma(a)}e^zz^{a-c}</math>


Now we can use this to rewrite our equation for <math>\Phi\!</math> of <math>\xi\!</math>:
<math>\dfrac{\alpha_{n+1}}{\alpha_n}= \left( \dfrac{a+n}{c+n} \right) \dfrac{1}{n+1}.</math>
:<math>\Phi(\xi)=Ae^{\frac{-\pi}{2}\lambda} \left[ \frac{e^{i\lambda \ln(k\xi)}}{\Gamma(1-i\lambda)} \left( 1-\frac{\lambda^2}{ik\xi} \right) +\frac{i\lambda}{ik\xi}\frac{e^{ik\xi+i\lambda \ln(k\xi)}}{\Gamma(1+i\lambda)} \right] </math>


Rewriting our wavefunction <math>\psi\!</math>:
Comparing this to what we obtained earlier, we find that <math>\Phi(\xi)</math> is
:<math>\psi(r,\theta)=\frac{Ce^{\frac{-\pi\lambda}{2}}}{\Gamma(1-i\lambda)} \left[ \left( 1-\frac{\lambda^2}{2ikr}\frac{1}{\sin^2\frac{\theta}{2}} \right) e^{ikz}e^{i\lambda \ln(k(r-z))}+\frac{f(\theta)}{r}e^{ikr+i\lambda \ln(2kr)} \right] </math>
where <math>f(\theta)\!</math> is the following:
:<math>f(\theta)=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)}\frac{1}{\sin^2\frac{\theta}{2}}e^{i\lambda \ln(\sin^2\frac{\theta}{2})}=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)} \left( \sin^2\frac{\theta}{2} \right) ^{i\lambda-1}</math>


We can then get our differential cross section from that by squaring it:
<math>\Phi(\xi)=A{}_1F_1(i\lambda,1,ik\xi),\!</math>
:<math>\frac{d\sigma}{d\Omega}=|f(\theta)|^2=\frac{\lambda^2}{4k^2\sin^4(\frac{\theta}{2})}=\frac{(Ze^2)^2}{16E^2}\frac{1}{\sin^4(\frac{\theta}{2})}</math>


If we normalize the wavefunction to give unit flux at large distances, we must take the following for the constant <math>C\!</math>:
where <math>A\!</math> is a c-number.
:<math>C=\sqrt{\frac{\mu}{\hbar k}}\Gamma(1-i\lambda)e^{\frac{\pi\lambda}{2}}</math>


So the wavefunction at large distances is given by the following:
The full wave function is thus
:<math>|\psi(0)|^2=|C|^2=\frac{\mu}{\hbar k}|\Gamma(1-i\lambda)|^2e^{\pi\lambda}</math>
 
where
<math>\psi(r,z)=A{}_1F_1(i\lambda,1,ik(r-z))e^{ikz}.\!</math>
:<math>|\Gamma(1-i\lambda)|^2=\frac{2\pi|\lambda|e^{-\pi\lambda}}{e^{2\pi\lambda}-1}</math>
 
In the limit, <math>z\to\infty,</math> the confluent hypergeometric function is approximately
 
<math>{}_1F_1(a,c,z)=\frac{\Gamma(c)(-z)^a}{\Gamma(c-a)} \left[ 1-\frac{a(a-c+1)}{z} \right] +\frac{\Gamma(c)}{\Gamma(a)}e^zz^{a-c}.</math>
 
We may use this to rewrite <math>\Phi\!</math> in the limit of large <math>\xi</math> as
 
<math>\Phi(\xi)=Ae^{\frac{-\pi}{2}\lambda} \left[ \frac{e^{i\lambda \ln(k\xi)}}{\Gamma(1-i\lambda)} \left( 1-\frac{\lambda^2}{ik\xi} \right) +\frac{i\lambda}{ik\xi}\frac{e^{ik\xi+i\lambda \ln(k\xi)}}{\Gamma(1+i\lambda)} \right].</math>
 
In the same limit, the full wave function <math>\psi\!</math> is
 
<math>\psi(r,\theta)=\frac{Ce^{\frac{-\pi\lambda}{2}}}{\Gamma(1-i\lambda)} \left[ \left( 1-\frac{\lambda^2}{2ikr}\frac{1}{\sin^2\frac{\theta}{2}} \right) e^{ikz}e^{i\lambda \ln(k(r-z))}+\frac{f(\theta)}{r}e^{ikr+i\lambda \ln(2kr)} \right],</math>
 
where <math>f(\theta)\!</math> is
 
<math>f(\theta)=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)}\frac{1}{\sin^2\frac{\theta}{2}}e^{i\lambda \ln(\sin^2\frac{\theta}{2})}=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)} \left( \sin^2\frac{\theta}{2} \right) ^{i\lambda-1}.</math>
 
The differential cross section is thus
:<math>\frac{d\sigma}{d\Omega}=|f(\theta)|^2=\frac{\lambda^2}{4k^2\sin^4(\frac{\theta}{2})}=\frac{(Ze^2)^2}{16E^2}\frac{1}{\sin^4(\frac{\theta}{2})}.</math>
 
Note that this is the same result that we would obtain in the <math>\alpha\to 0</math> limit of the Yukawa potential using the Born approximation, as well as from a classical calculation.
 
==The Gamow Factor==
 
We will now determine the relative probability of finding a particle at the origin to that of finding a particle in the incident beam, simply given by
 
<math>\left |\frac{\psi(0)}{\psi(\infty)}\right |^2.</math>
 
Since <math>{}_1F_1(a,c;0)=1,\!</math> the probability density at the origin is just
 
<math>|\psi(0)|^2=|C|^2.\!</math>
 
At large distances, on the other hand, the probability density is
 
<math>|\psi(\infty)|^2=\frac{|C|^2 e^{-\pi\lambda}}{|\Gamma(1-i\lambda)|^2}.</math>
 
Using the fact that
 
<math>|\Gamma(1-i\lambda)|^2=\frac{2\pi|\lambda|e^{-\pi\lambda}}{e^{2\pi\lambda}-1},</math>


Plugging this in for our wavefunction squared:
this becomes
:<math>|\psi(0)|^2=\frac{2\pi|\lambda|}{\frac{\hbar k}{\mu}|1-e^{2\pi\lambda}|}</math>


Now let's use the following quantity to represent the velocity:
<math>|\psi(\infty)|^2=\frac{|C|^2}{2\pi|\lambda|}(e^{2\pi\lambda}-1).</math>
:<math>\frac{\hbar k}{\mu}=v</math>


For small incident velocities, we can write:
We therefore obtain
:<math>|\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}</math>
:<math>|\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}e^{-\frac{2\pi Ze^2}{\hbar v}}</math>
where the first equation is for an attractive Coulomb potential, and the second equation is for a repulsive Coulomb potential.


The factor <math> G \equiv \frac{\pi Ze^2}{\hbar v} \! </math>, the exponent of <math> e^{-2\frac{\pi Ze^2}{\hbar v}} \!</math>, is known as the Gamow factor. The Gamow Factor or Gamow-Sommerfeld Factor, named after its discoverer George Gamow, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions. For example, nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier, but when George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.
<math>\left |\frac{\psi(0)}{\psi(\infty)}\right |^2=\frac{2\pi|\lambda|}{e^{2\pi\lambda}-1}.</math>


The Gamow factor for the Coulomb potential can also be obtained via the WKB method. Recall that
If we now define the velocity,
:<math> \theta \equiv e^{\frac{1}{\hbar} \int_a^b |p(x')|dx'} </math> and <math>p(x')=\sqrt{\frac{2m}{\hbar^2}(E-V(x'))}</math>


For a broad and high barrier, <math> \theta \gg 1 </math>, and
<math>\frac{\hbar k}{\mu}=v,</math>
:<math> T \approx \frac{1}{\theta^2} </math>.


In this case <math> \theta = e^{\frac{1}{\hbar} \int_{-a}^0 |p(x')|dx'} </math>
then this becomes


Using our previous potential <math> V(x')=\frac{Ze^2}{|x'|} </math> and <math> E=\frac{Ze^2}{a} </math> we get
<math>|\psi(0)|^2=\frac{2\pi Ze^2}{\hbar v}e^{-\frac{2\pi Ze^2}{\hbar v}}.</math>
:<math>\int_a^b |p(x')|dx' = \int_{-a}^0 \sqrt{\frac{2m}{\hbar^2}(|E|-\frac{Ze^2}{|x'|})}dx' = \frac{2mE}{\hbar} \int_{-a}^0 \sqrt{|1-\frac{a}{x'}|} dx'</math>
:<math> => \frac{\sqrt{2mE}}{\hbar}a \int_0^1 \sqrt{\frac{1}{u}-1}du = \frac{\sqrt{2mE}}{\hbar}a\frac{\pi}{2} = \frac{\sqrt{2m}}{\hbar}\frac{Ze^2 \sqrt{E}}{E} \frac{\pi}{2}</math>
:<math> = \frac{\sqrt{2m}}{\hbar} \frac{\pi}{2} \frac{Ze^2}{\sqrt{E}} =  \frac{\sqrt{2m}}{\hbar} \frac{\pi}{2} \frac{Ze^2}{\sqrt{\frac{1}{2}mv^2}} = \pi \frac{Ze^2}{{\hbar}v}</math>


So, as above, the transmission coefficient for small v is
The quantity <math> G=\frac{\pi Ze^2}{\hbar v}, \! </math> that appears in the exponential is known as the Gamow factor. The Gamow factor (or Gamow-Sommerfeld factor), named after its discoverer George Gamow, is measure of the probability that two nuclear particles will overcome the Coulomb barrier in order to undergo nuclear reactions, such as nuclear fusion.  Classically, there is almost no possibility for protons to fuse by overcoming the Coulomb barrier, but, when George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.
:<math> T \approx e^{\frac{-2\pi}{\hbar} \frac{Ze^2}{v}} </math>

Latest revision as of 13:58, 12 January 2014

Quantum Mechanics A
SchrodEq.png
Schrödinger Equation
The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.
Basic Concepts and Theory of Motion
UV Catastrophe (Black-Body Radiation)
Photoelectric Effect
Stability of Matter
Double Slit Experiment
Stern-Gerlach Experiment
The Principle of Complementarity
The Correspondence Principle
The Philosophy of Quantum Theory
Brief Derivation of Schrödinger Equation
Relation Between the Wave Function and Probability Density
Stationary States
Heisenberg Uncertainty Principle
Some Consequences of the Uncertainty Principle
Linear Vector Spaces and Operators
Commutation Relations and Simultaneous Eigenvalues
The Schrödinger Equation in Dirac Notation
Transformations of Operators and Symmetry
Time Evolution of Expectation Values and Ehrenfest's Theorem
One-Dimensional Bound States
Oscillation Theorem
The Dirac Delta Function Potential
Scattering States, Transmission and Reflection
Motion in a Periodic Potential
Summary of One-Dimensional Systems
Harmonic Oscillator Spectrum and Eigenstates
Analytical Method for Solving the Simple Harmonic Oscillator
Coherent States
Charged Particles in an Electromagnetic Field
WKB Approximation
The Heisenberg Picture: Equations of Motion for Operators
The Interaction Picture
The Virial Theorem
Commutation Relations
Angular Momentum as a Generator of Rotations in 3D
Spherical Coordinates
Eigenvalue Quantization
Orbital Angular Momentum Eigenfunctions
General Formalism
Free Particle in Spherical Coordinates
Spherical Well
Isotropic Harmonic Oscillator
Hydrogen Atom
WKB in Spherical Coordinates
Feynman Path Integrals
The Free-Particle Propagator
Propagator for the Harmonic Oscillator
Differential Cross Section and the Green's Function Formulation of Scattering
Central Potential Scattering and Phase Shifts
Coulomb Potential Scattering

We now consider the scattering of an electron from the Coulomb potential. This problem is important because it is relevant to the famous scattering experiment by Rutherford that showed that the atomic nucleus only makes up a very small fraction of the total size of an atom. We will first use the Born approximation to find the cross section for a Yukawa potential,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V_0\frac{e^{-\alpha r}}{r},}

which reduces to the Coulomb potential when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\to 0.} We will then find the exact cross section for the Coulomb potential, starting with the Schrödinger equation.

Scattering From a Yukawa Potential in the Born Approximation

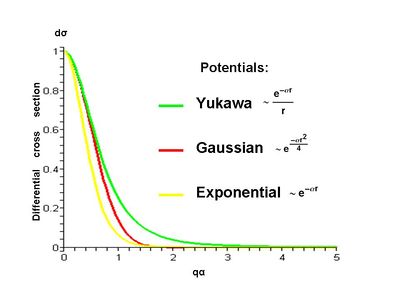
Comparison the differential cross sections for various potential type
Here we compare the differential cross sections for the Yukawa, Gaussian and exponential potential. We can see that for small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\alpha \!} all differential cross sections are similar. The differential cross section of the exponential potential decreases faster than the others and that of the Yukawa potential decreases more slowly than the others.

As alluded to earlier, let us first consider the Yukawa potential,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V_0\frac{e^{-\alpha r}}{r}.}

Within the Born approximation, the scattering amplitude is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f(\theta) &= -\frac{m}{2\pi\hbar^2}2\pi\int_0^\infty dr'\,r'^2 \frac{e^{-i|\mathbf{k}'-\mathbf{k}|r'}-e^{i|\mathbf{k}-\mathbf{k}'|r'}}{-i|\mathbf{k}'-\mathbf{k}|r'}\frac{V_0e^{-\alpha r'}}{r'} \\ &= -\frac{2mV_0}{\hbar^2}\int_0^\infty dr' r'^2 \frac{\sin\left(|\mathbf{k}'-\mathbf{k}|r'\right)}{|\mathbf{k}'-\mathbf{k}|r'}\frac{e^{-\alpha r'}}{r'} \\ &= -\frac{2mV_0}{\hbar^2}\frac{1}{\left(\left|\mathbf{k}'-\mathbf{k}\right|\right)^2+\alpha^2} \end{align} }

For the elastic scattering Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \mathbf{k} \right| = \left| \mathbf{k'} \right| = k \!} . Therefore,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\left|\mathbf{k}'-\mathbf{k}\right|)^2 = 2k\sin\frac{\theta}{2} }

and thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = -\frac{2mV_0}{\hbar^2}\frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}. }

The differential cross section is then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}= \left( \frac{2mV_0}{\hbar^2} \right) ^2 \left( \frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}\right)^2.}

Exact Coulomb Scattering Cross Section

Parabolic coordinates
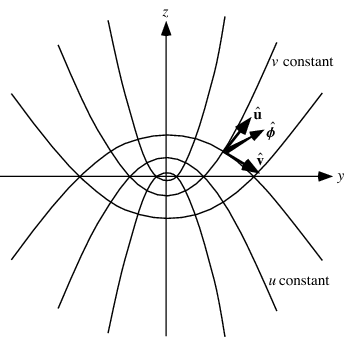
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} represents rotation about the z-axis, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} represents the parabolas with their vertices at a minimum, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\!} represents parabolas with their vertices at a maximum.

When we are considering scattering due to the Coulomb potential, we can not neglect the effect of this potential at large distances because it is only a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r}} potential.

We will work in parabolic coordinates, which are related to Cartesian coordinates by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=\sqrt{x^2+y^2+z^2}-z}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta=\sqrt{x^2+y^2+z^2}+z}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\tan^{-1}\left (\frac{y}{x}\right )}

The Schrödinger equation in parabolic coordinates is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ - \frac{\hbar^2}{2\mu}\frac{4}{\xi+\eta} \left( \frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{\xi+\eta}{4\xi\eta}\frac{\partial^2}{\partial \phi^2} \right) -\frac{2Ze^2}{\xi+\eta} \right] \psi=\frac{\hbar^2k^2}{2\mu}\psi.}

Recall that, for a spherically symmetric potential, the scattering amplitude is a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} only; therefore, we will seek solutions that are independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi.\!}

We will look for solution of the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\xi,\eta,\phi)=e^{\frac{i}{2}k(\eta-\xi)}\Phi(\xi)=e^{ikz}\Phi(r-z).}

The Schrödinger equation then becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \xi\frac{\partial^2}{\partial \xi^2}+(1-ik\xi)\frac{\partial}{\partial \xi}+\frac{Ze^2\mu}{k\hbar^2}k \right]\Phi(\xi)=0.}

We now assume a series solution,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=\sum_{n=0}^\infty a_n \xi^n.}

The recursion relation for the coefficients is then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{n+1}}{a_{n}}=\frac{in-\lambda}{(n+1)^2}k=\frac{n+i\lambda}{(n+1)^2}ik,}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{Ze^2\mu}{k\hbar^2}.}

Recall that the confluent hypergeometric function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {}_1F_1} is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=1+\frac{a}{c}z+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\dots+\frac{a(a+1)\dots(a+n-1)}{c(c+1)\dots(c+n-1)}\frac{z^n}{n!}+\dots}

The recursion formula for its coefficients is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\alpha_{n+1}}{\alpha_n}= \left( \dfrac{a+n}{c+n} \right) \dfrac{1}{n+1}.}

Comparing this to what we obtained earlier, we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=A{}_1F_1(i\lambda,1,ik\xi),\!}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\!} is a c-number.

The full wave function is thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,z)=A{}_1F_1(i\lambda,1,ik(r-z))e^{ikz}.\!}

In the limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\to\infty,} the confluent hypergeometric function is approximately

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {}_1F_1(a,c,z)=\frac{\Gamma(c)(-z)^a}{\Gamma(c-a)} \left[ 1-\frac{a(a-c+1)}{z} \right] +\frac{\Gamma(c)}{\Gamma(a)}e^zz^{a-c}.}

We may use this to rewrite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi\!} in the limit of large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=Ae^{\frac{-\pi}{2}\lambda} \left[ \frac{e^{i\lambda \ln(k\xi)}}{\Gamma(1-i\lambda)} \left( 1-\frac{\lambda^2}{ik\xi} \right) +\frac{i\lambda}{ik\xi}\frac{e^{ik\xi+i\lambda \ln(k\xi)}}{\Gamma(1+i\lambda)} \right].}

In the same limit, the full wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\!} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,\theta)=\frac{Ce^{\frac{-\pi\lambda}{2}}}{\Gamma(1-i\lambda)} \left[ \left( 1-\frac{\lambda^2}{2ikr}\frac{1}{\sin^2\frac{\theta}{2}} \right) e^{ikz}e^{i\lambda \ln(k(r-z))}+\frac{f(\theta)}{r}e^{ikr+i\lambda \ln(2kr)} \right],}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\!} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)}\frac{1}{\sin^2\frac{\theta}{2}}e^{i\lambda \ln(\sin^2\frac{\theta}{2})}=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)} \left( \sin^2\frac{\theta}{2} \right) ^{i\lambda-1}.}

The differential cross section is thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f(\theta)|^2=\frac{\lambda^2}{4k^2\sin^4(\frac{\theta}{2})}=\frac{(Ze^2)^2}{16E^2}\frac{1}{\sin^4(\frac{\theta}{2})}.}

Note that this is the same result that we would obtain in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\to 0} limit of the Yukawa potential using the Born approximation, as well as from a classical calculation.

The Gamow Factor

We will now determine the relative probability of finding a particle at the origin to that of finding a particle in the incident beam, simply given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\frac{\psi(0)}{\psi(\infty)}\right |^2.}

Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {}_1F_1(a,c;0)=1,\!} the probability density at the origin is just

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=|C|^2.\!}

At large distances, on the other hand, the probability density is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(\infty)|^2=\frac{|C|^2 e^{-\pi\lambda}}{|\Gamma(1-i\lambda)|^2}.}

Using the fact that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Gamma(1-i\lambda)|^2=\frac{2\pi|\lambda|e^{-\pi\lambda}}{e^{2\pi\lambda}-1},}

this becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(\infty)|^2=\frac{|C|^2}{2\pi|\lambda|}(e^{2\pi\lambda}-1).}

We therefore obtain

If we now define the velocity,

then this becomes

The quantity that appears in the exponential is known as the Gamow factor. The Gamow factor (or Gamow-Sommerfeld factor), named after its discoverer George Gamow, is measure of the probability that two nuclear particles will overcome the Coulomb barrier in order to undergo nuclear reactions, such as nuclear fusion. Classically, there is almost no possibility for protons to fuse by overcoming the Coulomb barrier, but, when George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Coulomb_Potential_Scattering&oldid=15659"