WKB Approximation: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
 
(37 intermediate revisions by 2 users not shown)
Line 1: Line 1:
WKB method (Wentzel-Kramers-Brillouin method) is a technique for finding approximations to certain differential equations, including the one dimensional [[Schrödinger equation]].   
{{Quantum Mechanics A}}
It was developed in 1926 by Wenzel, Kramers, and Brillouin, for whom it was named.  
The WKB (Wentzel-Kramers-Brillouin method) method is a technique for finding approximations to certain differential equations, including the one dimensional [[Schrödinger Equation|Schrödinger equation]].  It was developed in 1926 by Wenzel, Kramers, and Brillouin, for whom it was named. The logic behind this method is that, as <math>\hbar\rightarrow 0,\!</math> the wavelength, <math>\lambda=2\pi\hbar/ p,\!</math> tends to zero where the potential is smooth and slowly varying. Therefore, <math>\lambda\!</math> can be thought of as a local quantity <math>\lambda(x).\!</math> This is a semiclassical method of solving the Schrödinger equation.
The logic is that as <math>\hbar\rightarrow 0\!</math>, the wavelength, <math>\lambda=2\pi\hbar/ p\!</math>, tends to zero where the potential is smooth and slowly varying. Therefore, <math>\lambda\!</math> can be thought of as a local quantity <math>\lambda(x)\!</math>. This is a quasi-classical method of solving the Schrödinger equation.


In WKB, for a certain turning point, where <math>\lambda\!</math> is infinite, we cannot say that the potential changes slowly. Here, the whole theory is bound to fail, a proper handling of the turning points is the most difficult aspect of the WKB approximation. The potential at the turning point is approximated as linear and slowly varying (almost constant).  
However, for the classical turning points of the potential (i.e., where the energy of the particle becomes equal to the potential), <math>\lambda\!</math> becomes infinite, and we can no longer say that the potential changes slowly. Here, the whole theory is bound to fail.  A proper handling of the turning points is the most difficult aspect of the WKB approximation. In this case, the potential at the turning point is approximated as linear and slowly varying (almost constant).  


Through this way,  
By doing this, we can solve the Schrödinger equation and obtain the wave function in this "region". We can then use this wave function to connect the WKB wave functions at the two sides of the turning point.
:1. We can at least solve the Schrödinger equation and obtain the wave function in this "region". We can use this wave function to connect the WKB wave functions at the two sides of the turning point.
:2. We also need to know the region where the WKB wave functions are valid.


For <math>V(x) = 0\!</math> (or constant) the solutions to the Schrödinger equation are simply plane waves of the form <math> e^{\pm ikx} </math>. If the potential varies smoothly, and the energy of the particle is fixed, the wave function can be described locally by writing its plane wave form <math> e^{iu(x)} \!</math>.
==Derivation of the WKB Approximation==


The WKB solutions to the Schrödinger equation for a particle in a smoothly varying potential are given by:
For <math>V(x) = 0\!</math> (or constant) the solutions to the Schrödinger equation are simply plane waves of the form <math> e^{\pm ikx} </math>. If the potential varies smoothly, and the energy of the particle is fixed, the wave function can be described locally by writing its plane wave form <math> e^{iu(x)}\!</math>.  If we substitute this form into the Schrödinger equation, then we obtain


:<math>\psi(x)\approx \frac{C_\pm}{\sqrt{p(x)}}\exp\left[\pm \frac{i}{\hbar}\int_{x_0}^x p(x')dx'\right]</math>
<math>\left (\frac{du}{dx}\right )^2=\left [\frac{p(x)}{\hbar}\right ]^2+i\frac{d^2u}{dx^2},</math>


for a classically accessible region where E > V(x) and p(x) is real,
where <math>p(x)=\sqrt{2m[E-V(x)]}.</math>  Let us now assume that the second derivative on the right is small compared to the rest of the terms and neglect it as a first approximation.  Let us call this first approximation to <math>u(x)\!</math> <math>u_0(x).\!</math>  The equation satisfied by <math>u_0(x)\!</math> is


and written:
<math>\frac{du_0}{dx}=\pm\frac{p(x)}{\hbar}.</math>


:<math> \psi(x)\approx \frac{C_+}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{x_0}^x |p(x')|dx'\right] + \frac{C_-}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{x_0}^x |p(x')|dx'\right]</math>
Solving this equation, we obtain


for a classically inaccessible region where <math> E < V(x)\!</math>.
<math>u_0(x)=\pm\frac{1}{\hbar}\int_{x_0}^x dx'\,p(x')+C_0.</math>


In both cases <math>p(x)\!</math> is the classical formula for the momentum of a particle with total energy
We now use this first approximation to solve the full differential equation by an iterative process.  We obtain the next approximation by substituting <math>u_0(x)\!</math> into the right-hand side and solving for <math>u(x)\!</math> on the left.  If we call the result <math>u_1(x),\!</math> then the equation that we solve is
<math>E\!</math> and potential energy <math>V(x)\!</math> given by:


:<math>p(x)=\sqrt{2m(E-V(x))}\!</math>
<math>\frac{du_1}{dx}=\pm\sqrt{\left [\frac{p(x)}{\hbar}\right ]^2\pm\frac{i}{\hbar}\frac{dp}{dx}}.</math>


This is an exact solution if <math>V(x)\!</math> is constant, otherwise it's a local solution for a locally defined wavelength. There must be a condition on the region in space where the wavelength is locally defined to be sure the wavelength does not vary too much and the locally defined wave function is a valid approximation. This condition is that <math>\delta \lambda (x) \ll 1</math>, which is equivalent to writing <math> \left| \frac{d\lambda}{dx}\right|  = \left|\frac{d}{dx}\left(\frac{\hbar}{p(x)}\right)\right| \ll 1 </math>.
We must assume that <math>u_1(x)\!</math> has the same sign as <math>u_0(x)\!</math> in order for this iterative process to converge, and we must assume that <math>\frac{dp}{dx}\ll \frac{[p(x)]^2}{\hbar}</math> so that the deviation of <math>u_1(x)\!</math> from <math>u_0(x)\!</math> is small.  If this is the case, then we may assume that any further corrections introduced in further iterations are even smaller, and that <math>u_1(x)\!</math> is a good approximation to the exact solution. Under this assumption, we may expand the square root on the right-hand side of this equation, obtaining


<math>\frac{du_1}{dx}\approx\pm\frac{p(x)}{\hbar}+\frac{i}{p(x)}\frac{dp}{dx}.</math>


For example, suppose there is a point, <math> x = a \!</math>, which is a classical turning point at a given value of E and thereby separates the regions where <math> E > V(x)\!</math> and <math> E < V(x)\!</math>.  Let the classically inaccessible region be to the right of <math> a \!</math>.  In the region appropriately close to the turning point, the wave functions can be written as:
Solving this equation, we find that, for the classically accessible region, <math>E>V(x),\!</math> the WKB wave function is


<math>\psi(x)\approx \frac{C_+}{\sqrt{p(x)}}\exp\left [\frac{i}{\hbar}\int_{x_0}^x p(x')\,dx'\right ]+\frac{C_-}{\sqrt{p(x)}}\exp\left [-\frac{i}{\hbar}\int_{x_0}^x p(x')\,dx'\right ],</math>


:<math> \psi(x)\approx \frac{A}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{a}^x |p(x')|dx'\right]+ \frac{B}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{a}^x |p(x')|dx'\right] </math>
and for the classically forbidden region, <math>E<V(x),\!</math>  


for <math> x \gg a \! </math>,  and
<math>\psi(x)\approx \frac{C_+}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{x_0}^x |p(x')|\,dx'\right] + \frac{C_-}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{x_0}^x |p(x')|\,dx'\right].</math>


:<math> \psi(x)\approx \frac{C}{\sqrt{p(x)}}\exp\left[- \frac{i}{\hbar}\int_{a}^x p(x')dx'\right]+ \frac{D}{\sqrt{p(x)}}\exp\left[\frac{i}{\hbar}\int_{a}^x p(x')dx'\right] </math>
This is an exact solution if <math>V(x)\!</math> is constant, otherwise it is a local solution for a locally-defined wavelength. In order for this approximation to be valid, we must assume that the wavelength is slowly varying as a function of <math>x.\!</math> In other words, <math>\left |\frac{d\lambda}{dx}\right |=\left |\frac{d}{dx}\left(\frac{\hbar}{p(x)}\right)\right | \ll 1.</math>


for <math> x \ll a \!</math>.  
Let us now suppose that we let <math>x_0=a,\!</math> where <math>a\!</math> is a classical turning point at a given value of <math>E\!</math> and thereby separates a region where <math> E > V(x)\!</math> from a region where <math> E < V(x).\!</math> Let the classically inaccessible region be to the right of <math>a.\!</math>  For <math>x\!</math> sufficiently far away from <math>a,\!</math> the WKB wave function is


Note that at the classical turning point <math>p(a) = 0</math> and the WKB solution diverges, which means it is no longer a valid approximation because the true wave function will not exhibit such divergent behavior at the turning points.  Thus, around each turning point we need to splice the two WKB solutions on either side of the turning point with a "patching" function that will straddle each turning point.  Because we only need a solution for this function in the vicinity of the turning points, we can approximate the potential as being linear. If we center the turning point at the origin (<math> a = 0 \!</math>) we have:
<math> \psi(x)\approx \frac{A}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{a}^x |p(x')|\,dx'\right]+ \frac{B}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{a}^x |p(x')|\,dx'\right] </math>


:<math>
for <math> x \gg a, \! </math> and
V(x)\approx E+V'(0)x\!</math>


Solving the Schrödinger equation with our now linearized potential leads to the Airy equation whose solutions are Airy functions.
<math>  \psi(x)\approx \frac{C}{\sqrt{p(x)}}\exp\left[- \frac{i}{\hbar}\int_{a}^x p(x')\,dx'\right]+ \frac{D}{\sqrt{p(x)}}\exp\left[\frac{i}{\hbar}\int_{a}^x p(x')\,dx'\right] </math>
Our patching wave function is then:


:<math>
for <math> x \ll a. \!</math>
\psi_p(x)= C_1 \mathrm{Ai}\left(\alpha x\right)+ C_2 \mathrm{Bi}\left(\alpha x\right)\!</math>


where <math>C_1, C_2\!</math> are c-number coefficients and
==Patching the Wave Function Near a Classical Turning Point==


:<math>\alpha=\left(\frac{2m}{\hbar^2}V'(0)\right)^{\frac{1}{3}}</math>
Note that, at the classical turning point, <math>p(a) = 0\!</math> and the WKB solution diverges, meaning that it is no longer a valid approximation because the true wave function will not exhibit such divergent behavior at the turning points.  Thus, around each turning point, we need to splice the two WKB solutions on either side of the turning point with a "patching" function that will straddle each turning point.  Because we only need a solution for this function in the vicinity of the turning points, we can approximate the potential as being linear. If we center the turning point at the origin, i.e. we take <math>a=0,\!</math> the potential is approximately
 
<math>V(x)\approx E+V'(0)x.\!</math>
 
Solving the Schrödinger equation with this linearized potential leads to the Airy equation whose solutions are [http://mathworld.wolfram.com/AiryFunctions.html Airy functions].  Our patching wave function, which we denote by <math>\psi_p(x),\!</math> is then:
 
<math>\psi_p(x)= C_1 \mathrm{Ai}\left(\alpha x\right)+ C_2 \mathrm{Bi}\left(\alpha x\right)\!</math>
 
where <math>C_1\!</math> and <math>C_2\!</math> are complex number coefficients and
 
<math>\alpha=\left(\frac{2m}{\hbar^2}V'(0)\right)^{1/3}.</math>
   
   
The key to patching the wavefunction in the region of the turning point is to asymptotically match the patching wavefunction to the wavefunctions outside the region of the classical turning point. In the vicinity of the classical turning point,
The key to patching the wavefunction in the region of the turning point is to asymptotically match the patching wavefunction to the wavefunctions far away from the classical turning point. In the vicinity of the classical turning point,


:<math>p^2=2m(-V'(0)x)\Rightarrow 2p\frac{dp}{dx}=-2mV'(0)\Rightarrow \frac{dp}{dx}=-\frac{m}{p}V'(0) </math> <br/>
<math>p^2=2m(-V'(0)x)\Rightarrow 2p\frac{dp}{dx}=-2mV'(0)\Rightarrow \frac{dp}{dx}=-\frac{m}{p}V'(0) </math> <br/>


Since the region of applicability of the WKB approximation is
Since the region of applicability of the WKB approximation is
<math>1\gg\frac{1}{2\pi}\left|\frac{d\lambda}{dx}\right|</math>


near the turning point
<math>1\gg\frac{1}{2\pi}\left|\frac{d\lambda}{dx}\right|,</math>
 
we find that, near the turning point,
 
<math>|p|^3 \gg \hbar m|V'(0)|,</math>


:<math>|p|^3 \gg \hbar m|V'(0)|\Rightarrow |x|\gg \frac{\hbar^{\frac{2}{3}}}{2}|mV'(0)|^{-\frac{1}{3}} </math> <br/>
or
 
<math>|x|\gg \tfrac{1}{2}\hbar^{2/3}|mV'(0)|^{-1/3}.</math>
   
   
This implies that the width of the region around the classical turning point vanishes as <math>\hbar^{\frac{2}{3}}</math>.
This implies that the width of the region around the classical turning point vanishes as <math>\hbar^{2/3}.</math>  
Thus, we can come as close to the turning point as we wish with the WKB approximations by taking a limit as <math>\hbar\!</math> approaches zero, as long as the distance from the classical turning point is much less than <math>\hbar^{\frac{2}{3}}</math>. Thus, by extending the patching function towards singularity in the direction of the WKB approximated wavefunction, while simultaneously extending the WKB approximated wavefunction toward the classical turning point, it is possible to match the asymptotic forms of the wavefunctions from the two regions, which are then used to patch the wavefunctions together.
Thus, we can come as close to the turning point as we wish with the WKB approximation by taking the limit as <math>\hbar\!</math> approaches zero, as long as the distance from the classical turning point is much greater than <math>\hbar^{2/3}.</math> Thus, by extending the patching function towards the singularity in the WKB wave function, while simultaneously extending the WKB wave function toward the classical turning point, it is possible to match the asymptotic forms of the wave functions from the two regions, which are then used to patch them together.
   
   
This means that it would be useful to have a form of the Airy functions as they approach positive or negative infinity:
For this purpose, the following asymptotic forms of the Airy functions <math>\text{Ai}(z)\!</math> and <math>\text{Bi}(z)\!</math> as <math>z\rightarrow\pm\infty</math> will be useful:
   
   
:<math>z\rightarrow \infty: \mathrm{Ai}(z)\rightarrow \frac{1}{2\sqrt{\pi}}z^{-\frac{1}{4}}e^{-\frac{2}{3}|z|^{\frac{3}{2}}}</math><br/>
<math>z\rightarrow \infty: \mathrm{Ai}(z)\rightarrow \frac{1}{2\sqrt{\pi}}z^{-\frac{1}{4}}e^{-\frac{2}{3}|z|^{\frac{3}{2}}}</math><br/>
:<math>z\rightarrow \infty: \mathrm{Bi}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}e^{\frac{2}{3}|z|^{\frac{3}{2}}}</math><br/>
<math>z\rightarrow \infty: \mathrm{Bi}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}e^{\frac{2}{3}|z|^{\frac{3}{2}}}</math><br/>
:<math>z\rightarrow -\infty: \mathrm{Ai}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\cos\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)</math><br/>
<math>z\rightarrow -\infty: \mathrm{Ai}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\cos\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)</math><br/>
:<math>z\rightarrow -\infty: \mathrm{Bi}(z)\rightarrow -\frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\sin\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)</math>
<math>z\rightarrow -\infty: \mathrm{Bi}(z)\rightarrow -\frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\sin\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)</math>


And noticing that in the vicinity of the turning point (for negative <math>x\!</math>):
Noticing that in the vicinity of the turning point (for negative <math>x\!</math>),


:<math>\frac{1}{\hbar}\int_{x}^0p(x')dx'=\sqrt{\frac{2mV'(0)}{\hbar^2}} \int_x^0\sqrt{-x'}dx'=\frac{2}{3}\sqrt{\frac{2mV'(0)}{\hbar^2}}|x|^{\frac{3}{2}}=\frac{2}{3}|\alpha x|^{\frac{3}{2}}
<math>\frac{1}{\hbar}\int_{x}^0p(x')\,dx'=\sqrt{\frac{2mV'(0)}{\hbar^2}} \int_x^0\sqrt{-x'}\,dx'=\tfrac{2}{3}\sqrt{\frac{2mV'(0)}{\hbar^2}}|x|^{3/2}=\tfrac{2}{3}|\alpha x|^{3/2}
</math>  
</math>  


and
and
   
   
:<math>\frac{1}{\sqrt{p(x)}}=\left(2mV'(0)\right)^{-\frac{1}{4}}|x|^{-\frac{1}{4}}
<math>\frac{1}{\sqrt{p(x)}}=\left(2mV'(0)\right)^{-1/4}|x|^{-1/4},</math>  
</math>  
   
   
it becomes apparent that our WKB approximation of the wavefunction is the same as the patching function in the asymptotic limit.
it becomes apparent that the WKB approximation to the wave function is the same as the patching function in the asymptotic limit.
This must be the case, since as <math>\hbar\rightarrow 0</math> the region of invalidity of the semiclassical wavefunction in the vicinity of the turning point shrinks, while the solution of the linarized potential problem depends only on the accuracy of the linearity of the potential, and not on <math>\hbar</math>. The two regions must therefore overlap.  
This must be the case, since, as <math>\hbar\rightarrow 0,</math> the region of invalidity of the semiclassical wave function in the vicinity of the turning point shrinks, while the solution of the linarized potential problem depends only on the accuracy of the linearity of the potential, and not on <math>\hbar.</math> The two regions must therefore overlap.  


For example, one can take  <math>x\approx \hbar^{\frac{1}{3}}</math> and then take the limit <math>\hbar\rightarrow 0</math>. The semiclassical solution must hold as we are always in the region of its validity and so must the solution of the linearized potential problem. Note that the argument of the Airy functions at <math>x\approx \hbar^{\frac{1}{3}}</math> goes to <math>\pm\infty</math>, which is why we need their asymptotic expansion.
For example, one can take  <math>x\sim \hbar^{1/3}</math> and then take the limit <math>\hbar\rightarrow 0.</math> The semiclassical solution must hold as we are always in the region of its validity and so must the solution of the linearized potential problem. Note that the argument of the Airy functions at <math>x\sim \hbar^{1/3}</math> goes to <math>\pm\infty</math>, which is why we need their asymptotic expansion.


For a classical turning point <math>x=a\!</math> that separates a classically inaccessible region <math>x>a\!</math> from a classically accessible region <math>x<a,\!</math> we compare the WKB wave functions with the asymptotic expressions for the Airy functions and find that the WKB wave functions on the two sides of this turning point are connected as follows:


For a classical turning point x=a, which separate the classical inaccessible region x>a from the classical accessible region x<a, by comparing the WKB wave functions with the asymptotic expressions of the Airy functions, we find that the WKB wave functions on the two sides of the turning point x=a are connected as:
<math>
\frac{2A}{\sqrt{k(x)}}\cos\left (\int_{x}^{a}k(x')\,dx'-\frac{\pi}{4}\right )-\frac{B}{\sqrt{k(x)}}\sin\left (\int_{x}^{a}k(x')\,dx'-\frac{\pi}{4}\right ) \longleftrightarrow
\frac{A}{\sqrt{|k(x)|}}\exp\left (-\int_{a}^{x}|k(x')|\,dx'\right )+\frac{B}{\sqrt{|k(x)|}}\exp\left (\int_{a}^{x}|k(x')|\,dx'\right ),
</math>


:<math>
where <math>k(x)=\frac{p(x)}{\hbar}.</math>  Similarly, for a classical turning point <math>x=b,\!</math> that separates a classically accessible region <math>x>b\!</math> from a classically inaccessible region <math>x<b,\!</math> we find that the connection between the WKB wave functions on either side of the turning point is
\frac{2A}{\sqrt{k(x)}}\cos(\int_{x}^{a}k(x)dx-\frac{\pi}{4})-\frac{B}{\sqrt{k(x)}}\sin(\int_{x}^{a}k(x)dx-\frac{\pi}{4}) \longleftrightarrow
\frac{A}{\sqrt{|k(x)|}}exp(-\int_{a}^{x}|k(x)|dx)+\frac{B}{\sqrt{|k(x)|}}exp(\int_{a}^{x}|k(x)|dx)


<math>
\frac{2A}{\sqrt{k(x)}}\cos\left (\int_{b}^{x}k(x')\,dx'-\frac{\pi}{4}\right )-\frac{B}{\sqrt{k(x)}}\sin\left (\int_{b}^{x}k(x')\,dx'-\frac{\pi}{4}\right ) \longleftrightarrow
\frac{A}{\sqrt{|k(x)|}}\exp\left (-\int_{x}^{b}|k(x')|\,dx'\right )+\frac{B}{\sqrt{|k(x)|}}\exp\left (\int_{x}^{b}|k(x')|\,dx'\right ).
</math>
</math>


==Bound States Within the WKB Approximation==
We may use the WKB approximation to find the bound state energies of a potential, if any.  We will show that, in fact, we recover the Bohr-Sommerfeld quantization rule from the old quantum theory.  We will have, in effect, shown that the old quantum theory is in fact a semiclassical approximation to the modern quantum theory that we have been studying thus far.
Let us consider a potential with no rigid walls.  Let us also label the boundaries of the classically accessible region for a given energy <math>E\!</math> as <math>b\!</math> and <math>a,\!</math> such that the accessible region is <math>b<x<a.\!</math>  To the left of this region, the wave function of a bound state must have the form,
<math>\psi(x)=\frac{A}{\sqrt{|p(x)|}}\exp\left (-\frac{1}{\hbar}\int_x^b |p(x')|\,dx'\right ),</math>
in order for it to exponentially decay to zero as <math>x\rightarrow -\infty.</math>  Using the connection formulas derived earlier, we find that the wave function inside the classically accessible region is
<math>\psi(x)=\frac{2A}{\sqrt{|p(x)|}}\cos\left (\frac{1}{\hbar}\int_b^x p(x')\,dx'-\frac{\pi}{4}\right ).</math>
This may be rewritten as


On the other hand, for a classical turning point x=b, which separate the classical accessible region x>b from the classical inaccessible region x<b, by comparing the WKB wave functions with the asymptotic expressions of the Airy functions, we find that the WKB wave functions on the two sides of the turning point x=b are connected as:
<math>\psi(x)=\frac{2A}{\sqrt{|p(x)|}}\sin\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )\cos\left (\frac{1}{\hbar}\int_x^a p(x')\,dx'-\frac{\pi}{4}\right )-\frac{2A}{\sqrt{|p(x)|}}\cos\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )\sin\left (\frac{1}{\hbar}\int_x^a p(x')\,dx'-\frac{\pi}{4}\right ).</math>


:<math>
Again using the connection formulas, we see that the coefficient of the second term must vanish in order for the wave function for <math>x>a\!</math> to decay exponentially to zero as <math>x\rightarrow\infty;</math> i.e.,
\frac{2A}{\sqrt{k(x)}}\cos(\int_{b}^{x}k(x)dx-\frac{\pi}{4})-\frac{B}{\sqrt{k(x)}}\sin(\int_{b}^{x}k(x)dx-\frac{\pi}{4}) \longleftrightarrow
\frac{A}{\sqrt{|k(x)|}}exp(-\int_{x}^{b}|k(x)|dx)+\frac{B}{\sqrt{|k(x)|}}exp(\int_{x}^{b}|k(x)|dx)


</math>
<math>\cos\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )=0.</math>


This is satisfied if


<math>\int_b^a p(x)\,dx=\left (n+\tfrac{1}{2}\right )\pi\hbar.</math>


==Bohr-Sommerfeld Quantization Rule ==
A similar treatment for the case where one of <math>b\!</math> or <math>a\!</math> is a rigid wall rather than a simple classical turning point yields the condition,


The quantized energy levels of a bound state can be approximated by the WKB method with an expression known as the Bohr-Sommerfeld quantization rule. A particle in a potential well is subject to bound states. This common example of the WKB method can be found in most undergraduate level quantum texts.  
<math> \int_b^a p(x)\,dx = \left(n+\tfrac{3}{4}\right)\pi\hbar. </math>


For a potential with no rigid walls the Bohn-Sommerfeld Quantization rule is:
If both <math>b\!</math> and <math>a\!</math> are rigid walls, then we obtain


:<math>\oint p(x)dx = 2\int_{x_1}^{x_2}\sqrt{2m(E_n - V(x))}dx = \left(n+\frac{1}{2}\right)2\pi\hbar</math>
<math> \int_b^a p(x)\,dx = n\pi\hbar.</math>


For a potential with one rigid wall:
==Transmission and Reflection Through a Barrier==


:<math> \int_{x_1}^{x_2}\sqrt{2m(E_n - V(x))}dx = \left(n+\frac{3}{4}\right)\pi\hbar </math>
The WKB approximation can also be used to calculate transmission and reflection coefficients through a potential barrier.  In the presence of such a barrier, the wave function will have the form,


For a potential with two rigid walls:
<math>\psi(x)=
\begin{cases}
\frac{A}{\sqrt{|p(x)|}}\exp\left [\frac{i}{\hbar}\int_{a}^{x} p(x')\,dx'\right ]+\frac{B}{\sqrt{|p(x)|}}\exp\left [-\frac{i}{\hbar}\int_{a}^{x} p(x')\,dx'\right ], & x<a \\
\frac{C}{\sqrt{|p(x)|}}\exp\left [-\frac{1}{\hbar}\int_{a}^{x} |p(x')|\,dx'\right ]+\frac{D}{\sqrt{|p(x)|}}\exp\left [\frac{1}{\hbar}\int_{a}^{x} |p(x')|\,dx'\right ], & a<x<b \\
\frac{F}{\sqrt{|p(x)|}}\exp\left [\frac{i}{\hbar}\int_{b}^{x} p(x')\,dx'\right ]+\frac{G}{\sqrt{|p(x)|}}\exp\left [-\frac{i}{\hbar}\int_{b}^{x} p(x')\,dx'\right ], & x>b,
\end{cases}
</math>


:<math> \int_{x_1}^{x_2}\sqrt{2m(E_n - V(x))}dx = n\pi\hbar </math>
where, as usual, <math>a\!</math> and <math>b\!</math> are the classical turning points for the barrier.  If we now use the connection formulas derived earlier, we arrive at the relation,


For a central potential:
<math>
:<math> p_r^2 = E - V(r) - \frac{\hbar^2}{2m}\frac{\ell(\ell+1)}{r^2}</math>
\left [
:<math>
\begin{matrix}
\begin{align}
A \\
\int_{r_1}^{r_2}p_r(r)dr &= \int_{0}^{\infty}\sqrt{2m\left(E_n - V(r) - \frac{\hbar^2}{2m}\frac{\ell(\ell+1)}{r^2}\right)}dr \\
B
&= \left(n + \frac{1}{2}\right)\pi\hbar
\end{matrix}
\end{align}
\right ]=
\tfrac{1}{2}\left [
\begin{matrix}
2\theta+\frac{1}{2\theta} & i\left (2\theta-\frac{1}{2\theta}\right ) \\
-i\left (2\theta-\frac{1}{2\theta}\right ) & 2\theta+\frac{1}{2\theta}
\end{matrix}
\right ]
\left [
\begin{matrix}
F \\
G
\end{matrix}
\right ],
</math>
</math>


where
<math>\theta=\exp\left [\int_a^b |p(x)|\,dx\right ].</math>
The transmission coefficient is then defined in terms of the momentum right at the barrier, which will be the same on both sides, and is thus simply given by


[[Phy5645/WKBenergyspectrum|Worked Problem]]
<math>T=\left |\frac{F}{A}\right |^2.</math>


[[sample problem]]
If we now assume that there is no wave incident from the right, then <math>G=0\!</math> and
[[Worked by team]]


==WKB method for the Coulomb Potential ==
<math>T=\frac{4}{\left (2\theta+\frac{1}{2\theta}\right )^2}.</math>


For the coulomb potential, the potential is given by:
If the barrier is high and broad, then <math>\theta\ll 1,</math> so that we may approximate the transmission coefficient as
:<math> V(r) = -\frac{-Ze^2}{r} </math>


Since the electron is bound to the nucleus, it can be veiwed as moving between two rigid walls at <math> r = 0 \!</math> and <math> r = a \!</math> with energy <math> E = V(a), a = -\frac{-Ze^2}{E}\!</math>. Thus, the energy of the electron is negative.
<math>T\approx\frac{1}{\theta^2}=\exp\left [-2\int_a^b |p(x)|\,dx\right ].</math>


The energies of the s-state (<math> \ell = 0 \!</math>) can be obtained from:
==Problems==


:<math> \int_0^a \sqrt{2m\left(E+\frac{Ze^2}{r}\right)}dr = n\pi\hbar </math>
'''(1)''' Consider the potential,


Using the change of variable: <math> x = \frac{a}{r} </math>
<math> V(x) = V_{0}\ln\left (\frac{x}{a}\right ),\,x>0,</math>


:<math>  
where <math> V_{0} </math> and <math>a</math> are constants.  Assume that there is an infinite wall at <math>x=0.\!</math> Determine the bound states of this potential within the WKB approximation.  Show that the spacing between the levels is independent of mass.
\begin{align}
 
\int_0^a \sqrt{2m\left(E+\frac{Ze^2}{r}\right)}dr &= \sqrt{-2mE} \int_0^a dr \sqrt{\frac{a}{r} - 1} \\
[[Logarithmic Potential in WKB|Solution]]
&= a\sqrt{-2mE} \int_0^1 dx\sqrt{\frac{1}{x} - 1} \\
&= \frac{\pi}{2}a\sqrt{-2mE} \\
&= -Ze^2\pi\sqrt{-\frac{2m}{E}}
\end{align}
</math>


Where I have used the integal
[[Image:Gamow.jpg|thumb|500px]]
:<math> \int_0^1\sqrt{\frac{1}{x} -1} = \frac{\pi}{2} </math>
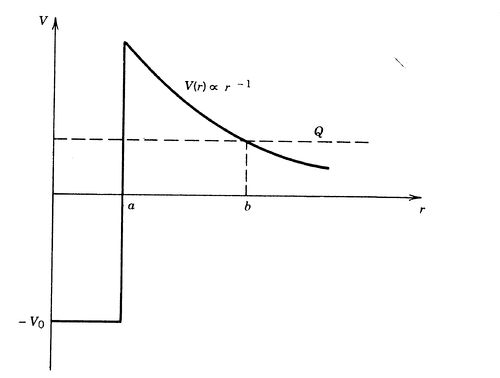
'''(2)''' Calculate the transmission probability for an alpha particle to tunnel through the Coulomb barrier of a nucleus of an atom with atomic number <math>Z.\!</math> The potential has the form,


Thus we have the expression:
<math>V(r)=\frac{2z_{1}e^{2}}{r},</math>
:<math>-Ze^2\pi\sqrt{-\frac{2m}{E}} = n\pi\hbar </math>
:<math>\Rightarrow E_n = -\frac{mZ^2e^4}{\hbar^2} = -\frac{Z^2e^2}{2a_0}</math>


Where <math> a_0\!</math> is the Bohr radius. Notice that this is the correct expression for the energy levels of a Coulomb potential.
for <math>r>a\!</math> and is constant for <math>r<a\!</math> (see figure).  In doing so, you will have calculated the (approximate) probability for a nucleus to undergo alpha decay. Note that the expression that you will obtain contains an exponential factor that is independent of <math>a;\!</math> this is known as the Gamow factor.


[[Phy5645/Gamowfactor|Calculation of Gamow factor using WKB Aprroximation Method]]
[[Phy5645/Gamowfactor|Solution]]

Latest revision as of 13:37, 18 January 2014

Quantum Mechanics A
SchrodEq.png
Schrödinger Equation
The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.
Basic Concepts and Theory of Motion
UV Catastrophe (Black-Body Radiation)
Photoelectric Effect
Stability of Matter
Double Slit Experiment
Stern-Gerlach Experiment
The Principle of Complementarity
The Correspondence Principle
The Philosophy of Quantum Theory
Brief Derivation of Schrödinger Equation
Relation Between the Wave Function and Probability Density
Stationary States
Heisenberg Uncertainty Principle
Some Consequences of the Uncertainty Principle
Linear Vector Spaces and Operators
Commutation Relations and Simultaneous Eigenvalues
The Schrödinger Equation in Dirac Notation
Transformations of Operators and Symmetry
Time Evolution of Expectation Values and Ehrenfest's Theorem
One-Dimensional Bound States
Oscillation Theorem
The Dirac Delta Function Potential
Scattering States, Transmission and Reflection
Motion in a Periodic Potential
Summary of One-Dimensional Systems
Harmonic Oscillator Spectrum and Eigenstates
Analytical Method for Solving the Simple Harmonic Oscillator
Coherent States
Charged Particles in an Electromagnetic Field
WKB Approximation
The Heisenberg Picture: Equations of Motion for Operators
The Interaction Picture
The Virial Theorem
Commutation Relations
Angular Momentum as a Generator of Rotations in 3D
Spherical Coordinates
Eigenvalue Quantization
Orbital Angular Momentum Eigenfunctions
General Formalism
Free Particle in Spherical Coordinates
Spherical Well
Isotropic Harmonic Oscillator
Hydrogen Atom
WKB in Spherical Coordinates
Feynman Path Integrals
The Free-Particle Propagator
Propagator for the Harmonic Oscillator
Differential Cross Section and the Green's Function Formulation of Scattering
Central Potential Scattering and Phase Shifts
Coulomb Potential Scattering

The WKB (Wentzel-Kramers-Brillouin method) method is a technique for finding approximations to certain differential equations, including the one dimensional Schrödinger equation. It was developed in 1926 by Wenzel, Kramers, and Brillouin, for whom it was named. The logic behind this method is that, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\rightarrow 0,\!} the wavelength, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=2\pi\hbar/ p,\!} tends to zero where the potential is smooth and slowly varying. Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda\!} can be thought of as a local quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda(x).\!} This is a semiclassical method of solving the Schrödinger equation.

However, for the classical turning points of the potential (i.e., where the energy of the particle becomes equal to the potential), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda\!} becomes infinite, and we can no longer say that the potential changes slowly. Here, the whole theory is bound to fail. A proper handling of the turning points is the most difficult aspect of the WKB approximation. In this case, the potential at the turning point is approximated as linear and slowly varying (almost constant).

By doing this, we can solve the Schrödinger equation and obtain the wave function in this "region". We can then use this wave function to connect the WKB wave functions at the two sides of the turning point.

Derivation of the WKB Approximation

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x) = 0\!} (or constant) the solutions to the Schrödinger equation are simply plane waves of the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\pm ikx} } . If the potential varies smoothly, and the energy of the particle is fixed, the wave function can be described locally by writing its plane wave form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{iu(x)}\!} . If we substitute this form into the Schrödinger equation, then we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (\frac{du}{dx}\right )^2=\left [\frac{p(x)}{\hbar}\right ]^2+i\frac{d^2u}{dx^2},}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(x)=\sqrt{2m[E-V(x)]}.} Let us now assume that the second derivative on the right is small compared to the rest of the terms and neglect it as a first approximation. Let us call this first approximation to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x)\!} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x).\!} The equation satisfied by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x)\!} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du_0}{dx}=\pm\frac{p(x)}{\hbar}.}

Solving this equation, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x)=\pm\frac{1}{\hbar}\int_{x_0}^x dx'\,p(x')+C_0.}

We now use this first approximation to solve the full differential equation by an iterative process. We obtain the next approximation by substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x)\!} into the right-hand side and solving for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x)\!} on the left. If we call the result Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_1(x),\!} then the equation that we solve is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du_1}{dx}=\pm\sqrt{\left [\frac{p(x)}{\hbar}\right ]^2\pm\frac{i}{\hbar}\frac{dp}{dx}}.}

We must assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_1(x)\!} has the same sign as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x)\!} in order for this iterative process to converge, and we must assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dp}{dx}\ll \frac{[p(x)]^2}{\hbar}} so that the deviation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_1(x)\!} from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0(x)\!} is small. If this is the case, then we may assume that any further corrections introduced in further iterations are even smaller, and that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_1(x)\!} is a good approximation to the exact solution. Under this assumption, we may expand the square root on the right-hand side of this equation, obtaining

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{du_1}{dx}\approx\pm\frac{p(x)}{\hbar}+\frac{i}{p(x)}\frac{dp}{dx}.}

Solving this equation, we find that, for the classically accessible region, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E>V(x),\!} the WKB wave function is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\approx \frac{C_+}{\sqrt{p(x)}}\exp\left [\frac{i}{\hbar}\int_{x_0}^x p(x')\,dx'\right ]+\frac{C_-}{\sqrt{p(x)}}\exp\left [-\frac{i}{\hbar}\int_{x_0}^x p(x')\,dx'\right ],}

and for the classically forbidden region, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E<V(x),\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\approx \frac{C_+}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{x_0}^x |p(x')|\,dx'\right] + \frac{C_-}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{x_0}^x |p(x')|\,dx'\right].}

This is an exact solution if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)\!} is constant, otherwise it is a local solution for a locally-defined wavelength. In order for this approximation to be valid, we must assume that the wavelength is slowly varying as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x.\!} In other words, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\frac{d\lambda}{dx}\right |=\left |\frac{d}{dx}\left(\frac{\hbar}{p(x)}\right)\right | \ll 1.}

Let us now suppose that we let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0=a,\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} is a classical turning point at a given value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\!} and thereby separates a region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E > V(x)\!} from a region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E < V(x).\!} Let the classically inaccessible region be to the right of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a.\!} For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\!} sufficiently far away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,\!} the WKB wave function is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\approx \frac{A}{\sqrt{|p(x)|}}\exp\left[- \frac{1}{\hbar}\int_{a}^x |p(x')|\,dx'\right]+ \frac{B}{\sqrt{|p(x)|}}\exp\left[\frac{1}{\hbar}\int_{a}^x |p(x')|\,dx'\right] }

for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \gg a, \! } and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\approx \frac{C}{\sqrt{p(x)}}\exp\left[- \frac{i}{\hbar}\int_{a}^x p(x')\,dx'\right]+ \frac{D}{\sqrt{p(x)}}\exp\left[\frac{i}{\hbar}\int_{a}^x p(x')\,dx'\right] }

for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \ll a. \!}

Patching the Wave Function Near a Classical Turning Point

Note that, at the classical turning point, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(a) = 0\!} and the WKB solution diverges, meaning that it is no longer a valid approximation because the true wave function will not exhibit such divergent behavior at the turning points. Thus, around each turning point, we need to splice the two WKB solutions on either side of the turning point with a "patching" function that will straddle each turning point. Because we only need a solution for this function in the vicinity of the turning points, we can approximate the potential as being linear. If we center the turning point at the origin, i.e. we take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=0,\!} the potential is approximately

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)\approx E+V'(0)x.\!}

Solving the Schrödinger equation with this linearized potential leads to the Airy equation whose solutions are Airy functions. Our patching wave function, which we denote by is then:

where and are complex number coefficients and

The key to patching the wavefunction in the region of the turning point is to asymptotically match the patching wavefunction to the wavefunctions far away from the classical turning point. In the vicinity of the classical turning point,


Since the region of applicability of the WKB approximation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1\gg\frac{1}{2\pi}\left|\frac{d\lambda}{dx}\right|,}

we find that, near the turning point,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |p|^3 \gg \hbar m|V'(0)|,}

or

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x|\gg \tfrac{1}{2}\hbar^{2/3}|mV'(0)|^{-1/3}.}

This implies that the width of the region around the classical turning point vanishes as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar^{2/3}.} Thus, we can come as close to the turning point as we wish with the WKB approximation by taking the limit as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\!} approaches zero, as long as the distance from the classical turning point is much greater than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar^{2/3}.} Thus, by extending the patching function towards the singularity in the WKB wave function, while simultaneously extending the WKB wave function toward the classical turning point, it is possible to match the asymptotic forms of the wave functions from the two regions, which are then used to patch them together.

For this purpose, the following asymptotic forms of the Airy functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Ai}(z)\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Bi}(z)\!} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\rightarrow\pm\infty} will be useful:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\rightarrow \infty: \mathrm{Ai}(z)\rightarrow \frac{1}{2\sqrt{\pi}}z^{-\frac{1}{4}}e^{-\frac{2}{3}|z|^{\frac{3}{2}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\rightarrow \infty: \mathrm{Bi}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}e^{\frac{2}{3}|z|^{\frac{3}{2}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\rightarrow -\infty: \mathrm{Ai}(z)\rightarrow \frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\cos\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\rightarrow -\infty: \mathrm{Bi}(z)\rightarrow -\frac{1}{\sqrt{\pi}}z^{-\frac{1}{4}}\sin\left(\frac{2}{3}|z|^{\frac{3}{2}}-\frac{\pi}{4}\right)}

Noticing that in the vicinity of the turning point (for negative Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\!} ),

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\hbar}\int_{x}^0p(x')\,dx'=\sqrt{\frac{2mV'(0)}{\hbar^2}} \int_x^0\sqrt{-x'}\,dx'=\tfrac{2}{3}\sqrt{\frac{2mV'(0)}{\hbar^2}}|x|^{3/2}=\tfrac{2}{3}|\alpha x|^{3/2} }

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{p(x)}}=\left(2mV'(0)\right)^{-1/4}|x|^{-1/4},}

it becomes apparent that the WKB approximation to the wave function is the same as the patching function in the asymptotic limit. This must be the case, since, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\rightarrow 0,} the region of invalidity of the semiclassical wave function in the vicinity of the turning point shrinks, while the solution of the linarized potential problem depends only on the accuracy of the linearity of the potential, and not on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar.} The two regions must therefore overlap.

For example, one can take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\sim \hbar^{1/3}} and then take the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\rightarrow 0.} The semiclassical solution must hold as we are always in the region of its validity and so must the solution of the linearized potential problem. Note that the argument of the Airy functions at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\sim \hbar^{1/3}} goes to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm\infty} , which is why we need their asymptotic expansion.

For a classical turning point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\!} that separates a classically inaccessible region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>a\!} from a classically accessible region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<a,\!} we compare the WKB wave functions with the asymptotic expressions for the Airy functions and find that the WKB wave functions on the two sides of this turning point are connected as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2A}{\sqrt{k(x)}}\cos\left (\int_{x}^{a}k(x')\,dx'-\frac{\pi}{4}\right )-\frac{B}{\sqrt{k(x)}}\sin\left (\int_{x}^{a}k(x')\,dx'-\frac{\pi}{4}\right ) \longleftrightarrow \frac{A}{\sqrt{|k(x)|}}\exp\left (-\int_{a}^{x}|k(x')|\,dx'\right )+\frac{B}{\sqrt{|k(x)|}}\exp\left (\int_{a}^{x}|k(x')|\,dx'\right ), }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k(x)=\frac{p(x)}{\hbar}.} Similarly, for a classical turning point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=b,\!} that separates a classically accessible region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>b\!} from a classically inaccessible region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<b,\!} we find that the connection between the WKB wave functions on either side of the turning point is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2A}{\sqrt{k(x)}}\cos\left (\int_{b}^{x}k(x')\,dx'-\frac{\pi}{4}\right )-\frac{B}{\sqrt{k(x)}}\sin\left (\int_{b}^{x}k(x')\,dx'-\frac{\pi}{4}\right ) \longleftrightarrow \frac{A}{\sqrt{|k(x)|}}\exp\left (-\int_{x}^{b}|k(x')|\,dx'\right )+\frac{B}{\sqrt{|k(x)|}}\exp\left (\int_{x}^{b}|k(x')|\,dx'\right ). }

Bound States Within the WKB Approximation

We may use the WKB approximation to find the bound state energies of a potential, if any. We will show that, in fact, we recover the Bohr-Sommerfeld quantization rule from the old quantum theory. We will have, in effect, shown that the old quantum theory is in fact a semiclassical approximation to the modern quantum theory that we have been studying thus far.

Let us consider a potential with no rigid walls. Let us also label the boundaries of the classically accessible region for a given energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\!} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,\!} such that the accessible region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b<x<a.\!} To the left of this region, the wave function of a bound state must have the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=\frac{A}{\sqrt{|p(x)|}}\exp\left (-\frac{1}{\hbar}\int_x^b |p(x')|\,dx'\right ),}

in order for it to exponentially decay to zero as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow -\infty.} Using the connection formulas derived earlier, we find that the wave function inside the classically accessible region is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=\frac{2A}{\sqrt{|p(x)|}}\cos\left (\frac{1}{\hbar}\int_b^x p(x')\,dx'-\frac{\pi}{4}\right ).}

This may be rewritten as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=\frac{2A}{\sqrt{|p(x)|}}\sin\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )\cos\left (\frac{1}{\hbar}\int_x^a p(x')\,dx'-\frac{\pi}{4}\right )-\frac{2A}{\sqrt{|p(x)|}}\cos\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )\sin\left (\frac{1}{\hbar}\int_x^a p(x')\,dx'-\frac{\pi}{4}\right ).}

Again using the connection formulas, we see that the coefficient of the second term must vanish in order for the wave function for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>a\!} to decay exponentially to zero as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow\infty;} i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\left (\frac{1}{\hbar}\int_b^a p(x')\,dx'\right )=0.}

This is satisfied if

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_b^a p(x)\,dx=\left (n+\tfrac{1}{2}\right )\pi\hbar.}

A similar treatment for the case where one of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\!} or is a rigid wall rather than a simple classical turning point yields the condition,

If both and are rigid walls, then we obtain

Transmission and Reflection Through a Barrier

The WKB approximation can also be used to calculate transmission and reflection coefficients through a potential barrier. In the presence of such a barrier, the wave function will have the form,

where, as usual, and are the classical turning points for the barrier. If we now use the connection formulas derived earlier, we arrive at the relation,

where

The transmission coefficient is then defined in terms of the momentum right at the barrier, which will be the same on both sides, and is thus simply given by

If we now assume that there is no wave incident from the right, then and

If the barrier is high and broad, then so that we may approximate the transmission coefficient as

Problems

(1) Consider the potential,

where and are constants. Assume that there is an infinite wall at Determine the bound states of this potential within the WKB approximation. Show that the spacing between the levels is independent of mass.

Solution

Gamow.jpg

(2) Calculate the transmission probability for an alpha particle to tunnel through the Coulomb barrier of a nucleus of an atom with atomic number The potential has the form,

for and is constant for (see figure). In doing so, you will have calculated the (approximate) probability for a nucleus to undergo alpha decay. Note that the expression that you will obtain contains an exponential factor that is independent of this is known as the Gamow factor.

Solution

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=WKB_Approximation&oldid=15811"