Motion in a Periodic Potential: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
No edit summary
 
(36 intermediate revisions by 2 users not shown)
Line 1: Line 1:
An example of a periodic potential is given in Figure 1 which consists of a series of continuous repeating form of potentials. In other words, the potential is translational symmetric over a certain period (in Figure 1 it is over period of <math>a\!</math>).  
{{Quantum Mechanics A}}
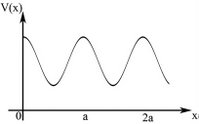
We will now consider the motion of electrons in periodic potentials.  An example of such a potential is given in Figure 1.


[[Image:periodic potential.jpg]]
[[Image:periodic potential.jpg]]


'''Figure 1.'''
'''Figure 1: An example of a periodic potential.'''


:<math> V(x)=V(x + a) \!</math>
A periodic potential is, by definition, translationally symmetric over a certain period (in Figure 1 it is over a period of <math>a\!</math>); i.e.,


In this case <math> a \!</math> is the period.
:<math> V(x)=V(x + a).\!</math>


The Hamiltonian of system under periodic potential commutes with the Translation Operator defined as:
In this case, <math>a\!</math> is the period.
:<math>\hat T_a\psi(x)=\psi(x+a)\!</math>
 
==Bloch's Theorem==
 
The Hamiltonian of a system with a periodic potential of period <math>a\!</math> commutes with translations by <math>a\!:</math>
:<math>\hat{T}_a\psi(x)=\psi(x+a)\!</math>
 
It is therefore possible to simultaneously diagonalize both the Hamiltonian and the translation operator.  We will now show that the eigenfunctions of the [[Schrödinger Equation|Schrödinger equation]] for this system,
 
:<math>\left [-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\right ]\psi(x)=E\psi(x),</math>
 
have the form,


This means that there is a simultaneous eigenstate of the Hamiltonian and the Translation Operator. The eigenfunction to the Schrödinger Equation,
:<math>\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right)\psi(x)=E\psi(x)</math>
has the form of the following,
:<math>\psi(x)=e^{ikx}u_k(x)\!</math>
:<math>\psi(x)=e^{ikx}u_k(x)\!</math>
where
where
:<math>u_k(x+a)=u_k(x)\!</math>
:<math>u_k(x+a)=u_k(x)\!</math>


This result is also known as the Bloch Theorem.
has the same period as the potential; this result is known as Bloch's theorem, and the eigenfunctions are called Bloch waves. To show this, we will prove that eigenfunctions of the translation operator, and thus of the Hamiltonian, have the above form.  Applying the translation operator to the proposed wave function, we find that
     
 
Also, by operating the <math>\hat T_a\!</math> operator on the wavefunction (also known as the Bloch wave), it can be seen that this waveform is also an eigenfunction of the <math>\hat T_a\!</math> operator, as shown in the following,
:<math>
:<math>
\begin{align}
\begin{align}
\hat T_a\psi(x)&=\hat T_a \left(e^{ikx}u_k(x)\right)\\
\psi(x+a)&=\hat{T}_a\psi(x) \\
&=\left(e^{ik(x+a)}u_k(x+a)\right)\\
&=\hat{T}_a\left [e^{ikx}u_k(x)\right ] \\
&=e^{ika}\left(e^{ikx}u_k(x)\right)\\
&=\left [e^{ik(x+a)}u_k(x+a)\right ] \\
&=e^{ika}\left [e^{ikx}u_k(x)\right ] \\
&=e^{ika}\psi(x)
&=e^{ika}\psi(x)
\end{align}</math>
\end{align}</math>
Using the same argument, it is clear that,
:<math>(\hat T_a)^n\psi(x)=e^{ikna}\psi(x)</math>


Also, note that if <math> k \!</math> is complex, then after multiple <math>\hat T_a\!</math> operations, the exponential will "blow-up". Thus, <math> k \!</math> has to be real. Applying the Bloch Theorem in solving Schrödinger Equation with known periodic potential will reveal interesting and important results such as a band gap opening in the Energy vs <math> k \!</math> spectrum. For materials with weak electron-electron interaction, given the Fermi energy of the system, one can then deduce whether such a system is metallic, semiconducting, or insulating.
We see that the proposed wave function is indeed an eigenfunction of the translation operator, with eigenvalue <math>e^{ika}.\!</math>  The quantity, <math>\hbar k,\!</math> is sometimes referred to as the crystal momentum, since it is a momentum-like quantity that characterizes the eigenstates of a system with discrete, rather than continuous, translational symmetry.
 
Also note that, if <math>k\!</math> is complex, then <math>\psi(x)\!</math> will diverge for <math>x\rightarrow\pm\infty,</math> with the choice of sign depending on the sign of the imaginary part of <math>k.\!</math>  Therefore, <math> k \!</math> has to be real if <math>\psi(x)\!</math> is to be a normalizable wave function.
 
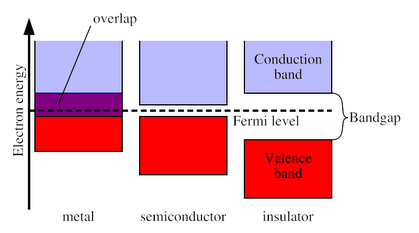
Applying Bloch's theorem to the [[Schrödinger Equation|Schrödinger equation]] for a given periodic potential will reveal interesting and important results, such as a "band" structure to the energy spectrum as a function of <math>k\!.</math> For materials with weak electron-electron interactions, one can then deduce, given the Fermi energy of the system, whether such a system is metallic (overlapping bands), semiconducting (small gap between bands), or insulating (large gap between bands) (see Figure 2).


[[Image:Insulator-metal.svg.png]]
[[Image:Insulator-metal.svg.png]]
Line 38: Line 50:
'''Figure 2. Energy band illustration showing the condition for metal, semiconductor, and insulator.'''
'''Figure 2. Energy band illustration showing the condition for metal, semiconductor, and insulator.'''


==Dirac Comb Potential==
As a simple example, let us consider a Dirac comb potential and the resulting [[Schrödinger Equation|Schrödinger equation]],


Consider for example the periodic potential and the resulting Schrödinger equation,
:<math>V(x)=V_0\sum_{n=-\infty}^{\infty}\delta(x-na)</math>
:<math>V(x)=V_0\sum_{n=-\infty}^{\infty}\delta(x-na)</math>
:<math>\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\right)\psi(x)=E\psi(x)</math>


Focusing the attention for case when <math> 0 < x < a \!</math>, the solution to the Schrödinger equation is of the form:
and
:<math>E=-\frac{\hbar^2q^2}{2m}</math>
 
:<math>\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\right)\psi(x)=E\psi(x).</math>
 
Let us focus on the region,<math> 0 < x < a,\!</math> since the wave function for all <math>x\!</math> may be obtained using Bloch's theorem.  Within this region, the equation simply reduces to that of a free particle, and thus the solution is
:<math>
:<math>
\begin{align}
\begin{align}
\psi(x) &= Ae^{iqx}+Be^{-iqx} \\
\psi_k(x) &= Ae^{iqx}+Be^{-iqx} \\
&= e^{ikx}\left(Ae^{i(q-k)x}+Be^{-i(q+k)x}\right) \\
&= e^{ikx}\left(Ae^{i(q-k)x}+Be^{-i(q+k)x}\right) \\
&= e^{ikx}u_k(x)
&= e^{ikx}u_k(x)
\end{align}
\end{align}
</math>
</math>
From periodicity and continuity with <math> \epsilon \rightarrow  0 </math>,
:<math>u_k(0 - \epsilon)=u_k(0 + \epsilon) = u_k(a + \epsilon)\!</math>


Thus, the wavefunction from <math> x < 0 \!</math> (left) and <math> x > 0 \! </math> (right) can be written as:
with energy <math>E=\frac{\hbar^2q^2}{2m}.</math>
:<math>\psi_r=e^{ikx}u_k(x)=e^{ikx}(Ae^{i(q-k)x}+Be^{-i(q+k)x})\!</math>
:<math>\psi_r=e^{ikx}u_k(x+a)=e^{ikx}(Ae^{i(q-k)(x+a)}+Be^{-i(q+k)(x+a)})\!</math>
When the continuity requirement at x = 0 is also being imposed, the following relation is found:
:<math>\psi_l(0)=\psi_r(0)\!</math>
:<math>A+B=Ae^{i(q-k)a}+Be^{-i(q+k)a}\!</math>   (1)


From differentiability and periodicity, the Schrödinger equation can be solved as the following:
Continuity of the wave function and the periodicity of <math>u_k\!</math> requires that
:<math>\int_{-\epsilon}^\epsilon -\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2}dx+\int_{-\epsilon}^\epsilon V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\psi(x)dx=\int_{-\epsilon}^\epsilon E \psi(x)dx</math>
where <math>\epsilon\!</math> is small, approaching zero. In this case, the term on the right hand side can be taken to be 0. Thus,
:<math>-\frac{\hbar^2}{2m}(\frac{\partial\psi_r(\epsilon)}{\partial x}-\frac{\partial\psi_l(-\epsilon)}{\partial x})=-V_0\psi_l(0)</math>
:<math>\lim_{\epsilon\to 0}(\frac{\partial\psi_r(\epsilon)}{\partial x}-\frac{\partial\psi_l(-\epsilon)}{\partial x})=\frac{2mV_0}{\hbar^2}\psi_l(0)</math>
where,
:<math>\lim_{\epsilon\to 0}\frac{\partial\psi_r(\epsilon)}{\partial x}=iq(A-B)</math>
:<math>\lim_{\epsilon\to 0}\frac{\partial\psi_l(-\epsilon)}{\partial x}=iq(Ae^{i(q-k)a}-Be^{-i(q+k)a})</math>


Evaluating further, the following condition is found:
:<math>\psi_k(a^{-})=\psi_k(a^{+})=e^{ika}\psi_k(0^{+}).\!</math>
:<math>iq(A-B-Ae^{i(q-k)a}+Be^{-i(q+k)a})=\frac{2mV_0}{\hbar^2}(A+B)</math> (2)


By simultaneously solving equation (1) and (2), the relationship between q and k is found to be:
Applying this condition to our wave function, we obtain
:<math>\cos(ka)=\cos(qa)+\frac{mV_0a}{\hbar^2}\frac{\sin(qa)}{qa}</math> (3)
:<math>Ae^{iqa}+Be^{-iqa}=e^{ika}(A+B).\!</math>   (1)


Worked Problem on Periodic Delta Function Potentials: [[Phy5645/Problem2|See Problem]]
Recall that the derivative of the wave function at a delta function potential is discontinuous, with the discontinuity given by
:<math>\psi'_k(a^{+})-\psi'_k(a^{-})=\frac{2mV_0}{\hbar^2}\psi_k(a).</math>


Where q is the energy band of the system, and k is the accessible energy band. By noting that the maximum value of the LHS is < the maximum value of the RHS of the relation above, it is clearly seen that there are some energy level that are not accessible as shown in Figure 3.
One may easily verify that the derivative of the wave function satisfies


[[Image:k_q relation graph.jpg]]
:<math>\psi'_k(x+a)=e^{ika}\psi'_k(x),\!</math>


Figure 3. Graph of Eq.(3). Wave is representing the LHS function, gray box representing the range of RHS function. Red lines is the forbidden solution, black line is the allowed solution.
so that
As k increases from 0 to  , there will be many solutions. Focusing only to two of the allowed solutions, it is seen that as k increases, there will be two solutions (one solution gives increasing q value, the other solution gives decreasing q value). Using the fact that the energy of the system is  , the dispersion relation (E vs. k) can be plotted as shown in Figure 4.
[[Image:dispersion relation small.jpg]]


Figure 4. Energy vs k showing the existence of band gap for system of an electron under periodic potential.
:<math>\psi'_k(a^{-})=\psi'_k(a^{+})=e^{ika}\psi'_k(0^{+}).\!</math>


Thus, in conjunction with Pauli exclusion principle, the single particle banspectrum such as the one we discussed here constitutes a simple description of band insulators and band metals.
We may now find the derivative of the wave function just to the left and just to the right of the delta function:


:<math>\psi'_k(a^{-})=iq(Ae^{iqa}-Be^{-iqa})\!</math>
:<math>\psi'_k(a^{+})=iqe^{ika}(A-B)\!</math>


We thus obtain
:<math>iq(Ae^{ika}-Be^{ika}-Ae^{iqa}+Be^{-iqa})=\frac{2mV_0}{\hbar^2}e^{ika}(A+B).</math>    (2)


If we take a more general case, where the potential is also periodic and always finite. The potential can be expressed as follows:
By requiring that Equations (1) and (2) have non-trivial solutions, we obtain the following relation between <math>q\!</math> and <math>k:\!</math>


:<math> V(x)=\begin{cases}
:<math>\cos(ka)=\cos(qa)+\frac{mV_0a}{\hbar^2}\frac{\sin(qa)}{qa}</math>    (3)


0, na<x<na+c;\\
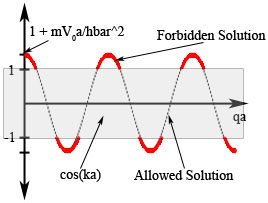
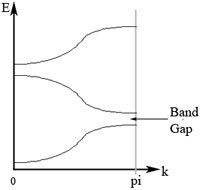
To obtain the energy bands, we now simply need to solve for <math>q\!</math> for a given value of <math>k\!</math> and substitute the result into the energy given above.  Since there can be multiple values of <math>q\!</math> that satisfy the above equation, we see that there are multiple "energy bands" in our system.  Note that the maximum value of the left-hand side of (3) is less than that of the right-hand side.  This implies that there are some values of <math>q\!</math> that cannot be obtained for any <math>k.\!</math>  The energies corresponding to these values of <math>q\!</math> are "forbidden bands" (see Fig. 3).  We sketch the energy bands of the system as a function of <math>k\!</math> in Fig. 4.


V_0, na+c<x<(n+1)a.
[[Image:k_q relation graph.jpg]]


\end{cases}
'''Figure 3. Sketch of the right-hand side of Equation (3).  The curve is the right-hand side, while the box represents the range of the left-hand side.  The solid red portions of the curve represent the forbidden bands, while the dashed black portions represent the allowed bands.'''
  </math>
   
[[Image:dispersion relation small.jpg]]


Further, we assume that the eigenfunction is:
'''Figure 4. Sketch of the energy bands for the Dirac comb potential as a function of <math>k.\!</math>  The band gap, corresponding to the forbidden energy bands, is labeled.'''


:<math>\psi_r=e^{ikx}u_k(x)\! </math>
We see that, in conjunction with Pauli exclusion principle, the single-particle band spectrum of a periodic potential, such as the one we discussed here, gives us a simple description of band insulators and band metals.


Then this problem is converted to seeking for <math>u_k(x)\!</math> in the region -b<x<c and connecting the wave function in different periods.
==Problem==


:<math>\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\right)\psi(x)=E_k\psi(x), 0<x<c</math>
Let us now consider a more general case, namely a square wave potential, given by


:<math>\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V_0\right)\psi(x)=E_k\psi(x), -b<x<0</math>
:<math> V(x)=\begin{cases}
 
0, & na < x < na+c \\
Further we assume that
V_0, & na+c < x < (n+1)a,
 
\end{cases}
:<math> k_1^2=\frac{2mE_k}{\hbar^2}, k_2^2=\frac{2m(V_0-E_k)}{\hbar^2} </math>
 
Then we can get the equation for <math> u_k(x)\!</math>:
 
:<math> \frac{d^2u_k(x)}{x^2}+2ik\frac{du_(x)}{dx}+(k_1^2-k^2)u(x)=0, 0<x<c </math>
 
:<math> \frac{d^2u_k(x)}{x^2}+2ik\frac{du_(x)}{dx}-(k_2^2+k^2)u(x)=0, -b<x<0 </math>
 
Solve for <math> u_k(x) \!</math>, we get:
 
:<math> u_k(x)=A_0e^{i(k_1-k)x}+B_0e^{-i(k_1+k)x}, 0<x<c </math>
 
:<math> u_k(x)=C_0e^{(k_2-ik)x}+D_0e^{-(k_2+ik)x}, -b<x<o </math>
 
By the continuity of <math> \psi(x) \!</math> and <math> \frac{d\psi(x)}{dx}</math> at <math> x=0 \!</math>:
 
:<math> A_0+B_0=C_0+D_0 \!</math>
 
:<math> i(k_1-k)A_0-i(k_1+k)B_0=(k_2-ik)C_0-(k_2+ik)D_0 \!</math>
 
By periodicity of <math> u_k(x) \!</math>, we get:
 
:<math> u_k(x)=u_k(x+a) \!</math>
 
:<math>C_0e^{(k_2-ik)x}+D_0e^{-(k_2+ik)x}=C_1e^{(k_2-ik)(x+a)}+D_1e^{-(k_2+ik)(x+a)}</math>
 
:<math>C_1=C_0e^{-(k_1-ik)a}</math>
 
:<math>D_1=D_0e^{(k_2+ik)a}</math>
 
By the continuity of <math> \psi(x) \!</math> and <math> \frac{d\psi(x)}{dx}\!</math> at <math> x=c \!</math>:
 
:<math>
\begin{align}
A_0&e^{i(k_1-k)x}+B_0e^{-i(k_2+k)x} \\
&=C_1e^{(k_2-ik)c}+D_1e^{-(k_2+ik)c}\\
&=C_0e^{-(k_2-ik)b}+D_0e^{(k_2+ik)b}
\end{align}
</math>
</math>


:<math>  
where <math>n\!</math> runs over all integers.  Determine the energy spectrum for this potential and show that it reduces to the result for the Dirac comb when <math>c\rightarrow a\!</math> and <math>V_0\rightarrow\infty\!</math> in such a way that the product, <math>V_0(c-a),\!</math> remains finite.
\begin{align}
i(k_1-k)&e^{i(k_1-k)c}A_0-i(k_1+k)e^{i(k_1+k)c}B_0 \\
= (k_2 &-ik)e^{(k_2-ik)c}C_1-(k_2+ik)e^{-(k_2+ik)c}D_1 \\
= (k_2 &-ik)e^{-(k_2-ik)b}C_0-(k_2+ik)e^{(k_2+ik)b}D_0
\end{align}
</math>
 
Now, we get four linear equations of <math>A_0, B_0, C_0 \!</math> and <math> D_0 \!</math>, to get the nontrivial solution, we have to make the determinant be zero:
 
:<math> \frac{k_2^2-k_1^2}{2k_1k_2}\sinh(k_2b)\sin(k_1c)+\cosh(k_2b)\cos(k_1c)=\cos(ka) </math>
 
This is the equation that the energy follows, where <math> k_1^2=\frac{2mE_k}{\hbar^2}\!</math> and <math> k_2^2=\frac{2m(V_0-E_k)}{\hbar^2} \!</math>.
 
If we take the limit <math> V_0 \rightarrow 0 \!</math> and <math> b \rightarrow 0 \!</math> and maintain <math>V_0b\!</math> finite, then we can obtain:
 
:<math> k_2=\sqrt{\frac{2m}{\hbar^2}(V_0-E_k)b^2} \simeq\sqrt{(V_0b)\frac{2mb}{\hbar^2}}\ll 1</math>
 
:<math>sinh(k_2b) \simeq k_2b </math>
 
:<math> cosh(k_2b) \simeq 1</math>
 
Hence we get:
 
:<math>\cos(ka)=\cos(k_1a)+\frac{mV_0ab}{\hbar^2}\frac{\sin(k_1a)}{k_1a}</math>


This equation is the same as the equation we obtain on the condition of periodic delta potential. And we should be aware that <math>V_0b</math> is finite and stand for the <math> V_0 </math> in the previous problem.
[[Phy5645/Square Wave Potential Problem|Solution]]

Latest revision as of 13:32, 18 January 2014

Quantum Mechanics A
SchrodEq.png
Schrödinger Equation
The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.
Basic Concepts and Theory of Motion
UV Catastrophe (Black-Body Radiation)
Photoelectric Effect
Stability of Matter
Double Slit Experiment
Stern-Gerlach Experiment
The Principle of Complementarity
The Correspondence Principle
The Philosophy of Quantum Theory
Brief Derivation of Schrödinger Equation
Relation Between the Wave Function and Probability Density
Stationary States
Heisenberg Uncertainty Principle
Some Consequences of the Uncertainty Principle
Linear Vector Spaces and Operators
Commutation Relations and Simultaneous Eigenvalues
The Schrödinger Equation in Dirac Notation
Transformations of Operators and Symmetry
Time Evolution of Expectation Values and Ehrenfest's Theorem
One-Dimensional Bound States
Oscillation Theorem
The Dirac Delta Function Potential
Scattering States, Transmission and Reflection
Motion in a Periodic Potential
Summary of One-Dimensional Systems
Harmonic Oscillator Spectrum and Eigenstates
Analytical Method for Solving the Simple Harmonic Oscillator
Coherent States
Charged Particles in an Electromagnetic Field
WKB Approximation
The Heisenberg Picture: Equations of Motion for Operators
The Interaction Picture
The Virial Theorem
Commutation Relations
Angular Momentum as a Generator of Rotations in 3D
Spherical Coordinates
Eigenvalue Quantization
Orbital Angular Momentum Eigenfunctions
General Formalism
Free Particle in Spherical Coordinates
Spherical Well
Isotropic Harmonic Oscillator
Hydrogen Atom
WKB in Spherical Coordinates
Feynman Path Integrals
The Free-Particle Propagator
Propagator for the Harmonic Oscillator
Differential Cross Section and the Green's Function Formulation of Scattering
Central Potential Scattering and Phase Shifts
Coulomb Potential Scattering

We will now consider the motion of electrons in periodic potentials. An example of such a potential is given in Figure 1.

Periodic potential.jpg

Figure 1: An example of a periodic potential.

A periodic potential is, by definition, translationally symmetric over a certain period (in Figure 1 it is over a period of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} ); i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=V(x + a).\!}

In this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} is the period.

Bloch's Theorem

The Hamiltonian of a system with a periodic potential of period Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} commutes with translations by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!:}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T}_a\psi(x)=\psi(x+a)\!}

It is therefore possible to simultaneously diagonalize both the Hamiltonian and the translation operator. We will now show that the eigenfunctions of the Schrödinger equation for this system,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\right ]\psi(x)=E\psi(x),}

have the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=e^{ikx}u_k(x)\!}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(x+a)=u_k(x)\!}

has the same period as the potential; this result is known as Bloch's theorem, and the eigenfunctions are called Bloch waves. To show this, we will prove that eigenfunctions of the translation operator, and thus of the Hamiltonian, have the above form. Applying the translation operator to the proposed wave function, we find that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi(x+a)&=\hat{T}_a\psi(x) \\ &=\hat{T}_a\left [e^{ikx}u_k(x)\right ] \\ &=\left [e^{ik(x+a)}u_k(x+a)\right ] \\ &=e^{ika}\left [e^{ikx}u_k(x)\right ] \\ &=e^{ika}\psi(x) \end{align}}

We see that the proposed wave function is indeed an eigenfunction of the translation operator, with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ika}.\!} The quantity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar k,\!} is sometimes referred to as the crystal momentum, since it is a momentum-like quantity that characterizes the eigenstates of a system with discrete, rather than continuous, translational symmetry.

Also note that, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is complex, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\!} will diverge for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow\pm\infty,} with the choice of sign depending on the sign of the imaginary part of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.\!} Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \!} has to be real if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\!} is to be a normalizable wave function.

Applying Bloch's theorem to the Schrödinger equation for a given periodic potential will reveal interesting and important results, such as a "band" structure to the energy spectrum as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!.} For materials with weak electron-electron interactions, one can then deduce, given the Fermi energy of the system, whether such a system is metallic (overlapping bands), semiconducting (small gap between bands), or insulating (large gap between bands) (see Figure 2).

Insulator-metal.svg.png

Figure 2. Energy band illustration showing the condition for metal, semiconductor, and insulator.

Dirac Comb Potential

As a simple example, let us consider a Dirac comb potential and the resulting Schrödinger equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=V_0\sum_{n=-\infty}^{\infty}\delta(x-na)}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\right)\psi(x)=E\psi(x).}

Let us focus on the region,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < x < a,\!} since the wave function for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\!} may be obtained using Bloch's theorem. Within this region, the equation simply reduces to that of a free particle, and thus the solution is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi_k(x) &= Ae^{iqx}+Be^{-iqx} \\ &= e^{ikx}\left(Ae^{i(q-k)x}+Be^{-i(q+k)x}\right) \\ &= e^{ikx}u_k(x) \end{align} }

with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\frac{\hbar^2q^2}{2m}.}

Continuity of the wave function and the periodicity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k\!} requires that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k(a^{-})=\psi_k(a^{+})=e^{ika}\psi_k(0^{+}).\!}

Applying this condition to our wave function, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ae^{iqa}+Be^{-iqa}=e^{ika}(A+B).\!} (1)

Recall that the derivative of the wave function at a delta function potential is discontinuous, with the discontinuity given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_k(a^{+})-\psi'_k(a^{-})=\frac{2mV_0}{\hbar^2}\psi_k(a).}

One may easily verify that the derivative of the wave function satisfies

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_k(x+a)=e^{ika}\psi'_k(x),\!}

so that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_k(a^{-})=\psi'_k(a^{+})=e^{ika}\psi'_k(0^{+}).\!}

We may now find the derivative of the wave function just to the left and just to the right of the delta function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_k(a^{-})=iq(Ae^{iqa}-Be^{-iqa})\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_k(a^{+})=iqe^{ika}(A-B)\!}

We thus obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iq(Ae^{ika}-Be^{ika}-Ae^{iqa}+Be^{-iqa})=\frac{2mV_0}{\hbar^2}e^{ika}(A+B).} (2)

By requiring that Equations (1) and (2) have non-trivial solutions, we obtain the following relation between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k:\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(ka)=\cos(qa)+\frac{mV_0a}{\hbar^2}\frac{\sin(qa)}{qa}} (3)

To obtain the energy bands, we now simply need to solve for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\!} for a given value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} and substitute the result into the energy given above. Since there can be multiple values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\!} that satisfy the above equation, we see that there are multiple "energy bands" in our system. Note that the maximum value of the left-hand side of (3) is less than that of the right-hand side. This implies that there are some values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\!} that cannot be obtained for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.\!} The energies corresponding to these values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\!} are "forbidden bands" (see Fig. 3). We sketch the energy bands of the system as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} in Fig. 4.

K q relation graph.jpg

Figure 3. Sketch of the right-hand side of Equation (3). The curve is the right-hand side, while the box represents the range of the left-hand side. The solid red portions of the curve represent the forbidden bands, while the dashed black portions represent the allowed bands.

Dispersion relation small.jpg

Figure 4. Sketch of the energy bands for the Dirac comb potential as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.\!} The band gap, corresponding to the forbidden energy bands, is labeled.

We see that, in conjunction with Pauli exclusion principle, the single-particle band spectrum of a periodic potential, such as the one we discussed here, gives us a simple description of band insulators and band metals.

Problem

Let us now consider a more general case, namely a square wave potential, given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=\begin{cases} 0, & na < x < na+c \\ V_0, & na+c < x < (n+1)a, \end{cases} }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} runs over all integers. Determine the energy spectrum for this potential and show that it reduces to the result for the Dirac comb when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\rightarrow a\!} and in such a way that the product, remains finite.

Solution

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Motion_in_a_Periodic_Potential&oldid=15797"