Stern-Gerlach Experiment: Difference between revisions

	Quantum Mechanics A
	Schrödinger Equation; The most fundamental equation of quantum mechanics; given a Hamiltonian , it describes how a state evolves in time.
	Physical Basis of Quantum Mechanics
	Basic Concepts and Theory of Motion; UV Catastrophe (Black-Body Radiation); Photoelectric Effect; Stability of Matter; Double Slit Experiment; Stern-Gerlach Experiment; The Principle of Complementarity; The Correspondence Principle; The Philosophy of Quantum Theory
	Schrödinger Equation
	Brief Derivation of Schrödinger Equation; Relation Between the Wave Function and Probability Density; Stationary States; Heisenberg Uncertainty Principle; Some Consequences of the Uncertainty Principle
	Operators, Eigenfunctions, and Symmetry
	Linear Vector Spaces and Operators; Commutation Relations and Simultaneous Eigenvalues; The Schrödinger Equation in Dirac Notation; Transformations of Operators and Symmetry; Time Evolution of Expectation Values and Ehrenfest's Theorem
	Motion in One Dimension
	One-Dimensional Bound States; Oscillation Theorem; The Dirac Delta Function Potential; Scattering States, Transmission and Reflection; Motion in a Periodic Potential; Summary of One-Dimensional Systems
	Discrete Eigenvalues and Bound States
	Harmonic Oscillator Spectrum and Eigenstates; Analytical Method for Solving the Simple Harmonic Oscillator; Coherent States; Charged Particles in an Electromagnetic Field; WKB Approximation
	Time Evolution and the Pictures of Quantum Mechanics
	The Heisenberg Picture: Equations of Motion for Operators; The Interaction Picture; The Virial Theorem
	Angular Momentum
	Commutation Relations; Angular Momentum as a Generator of Rotations in 3D; Spherical Coordinates; Eigenvalue Quantization; Orbital Angular Momentum Eigenfunctions
	Central Forces
	General Formalism; Free Particle in Spherical Coordinates; Spherical Well; Isotropic Harmonic Oscillator; Hydrogen Atom; WKB in Spherical Coordinates
	The Path Integral Formulation of Quantum Mechanics
	Feynman Path Integrals; The Free-Particle Propagator; Propagator for the Harmonic Oscillator
	Continuous Eigenvalues and Collision Theory
	Differential Cross Section and the Green's Function Formulation of Scattering; Central Potential Scattering and Phase Shifts; Coulomb Potential Scattering

Latest revision as of 13:36, 8 August 2013

Preformed in 1922 by Walter Stern and Otto Gerlach, this experiment demonstrated that particles have intrinsic spin. A collimated monochromatic beam of silver atoms (Ag) is subjected to an inhomogeneous magnetic field. Silver was chosen because it has all of its shells full except for one additional electron in the $5s\!$ shell. It is necessary to use a non-uniform magnetic field because, if the field was uniform, the trajectory of the silver atoms would be unaffected. In a non-uniform field the force on one end of the dipole is greater than the other.

Classical theory would predict that there would be a continuous line at the collector plate because the orientation of the spin would be completely random. However, at the collector there was only two spots. The atoms were deflected in the vertical direction by specific amount equal to $\pm \hbar /2$ , thus showing that spin is quantized. Because there were only two spots at the collector, we conclude that the electron is a spin ½ particle.

It is important to note here that this spin does not arise because the particle is spinning. If this were the case, then it would mean that parts of the spinning electron would be moving faster than the speed of light.

History

While our present understanding of the Stern-Gerlach experiment is that it demonstrates the fact that electrons have spin, one must keep in mind that the experiment was performed in 1922, three years before the concept of electronic spin was introduced and four years before modern quantum theory was introduced. As a matter of fact, the results of this experiment were originally taken as a confirmation of the old quantum theory of Bohr and Sommerfeld.

Sommerfeld, in the old quantum theory, had predicted the spatial quantization of trajectories and the directional quantization in a magnetic field $B\!$ . He knew that the magnetic moment $\mu =\gamma L\!$ , where the orbital gyromagnetic ratio $\gamma =q/2m.\!$ Sommerfeld understood the principle of the experiment as soon as 1918. And he expected a lot from it because it would have been the first proof of quantization in a non-radiative process.

One could argue, however, that there should be three spots and not two. Imagine an electron in a circular uniform motion around a proton. The $z$ component of angular momentum is quantized to integer multiples of $\hbar$ . In a magnetic field, the plane of the trajectory could have three directions corresponding, respectively, to an angular momentum parallel, antiparallel, or perpendicular to the field $B\!$ with $L_{z}=\hbar ,$ $L_{z}=-\hbar ,$ or $L_{z}=0.\!$

This is not the case - as soon as 1918, Bohr proved that the trajectory for which $L_{z}=0\!$ was unstable. One must, therefore, only observe two spots, corresponding to $L_{z}=\pm \hbar \!$ . This is exactly what Stern and Gerlach observed.

Furthermore, by measuring $\mu _{0}\!$ , they found that, to a few percent, the magnetic moment of an atom was

\mu _{0}=\left|\gamma _{0}^{orb}\right|\hbar ={\frac {q\hbar }{2m_{e}}},

as predicted by Bohr and Sommerfeld. Therefore, it was believed that the experiment had confirmed the old quantum theory. However, in our modern quantum theory, $L_{z}\!$ may be zero, which would appear to contradict the results of the Stern-Gerlach experiment. However, if one accounts for electronic spin, then one will correctly predict two spots.

Problem

(Double Pinhole Experiment)

Besides the Stern-Gerlach experiment, the double slit experiment also demonstrates the difference between quantum mechanics and classical mechanics. However, let us instead consider a double pinhole experiment rather than a double slit experiment because the former is mathematically simpler and still embodies the basic physics that we wish to demonstrate.

Suppose that a beam of electrons, traveling along the $z\!$ axis, hits a screen at $z=0\!$ with two pinholes at $x=0,y=\pm d/2$ . For a point $(x,y)\!$ on a second screen at $z=L>>d,\lambda \!$ , the distance from each pinhole is given by $r_{\pm }={\sqrt {x^{2}+(y\mp d/2)^{2}+L^{2}}}.$ A spherical wave is emitted from each pinhole; the waves from each add, and the wave function at a given point on the second screen is

\psi (x,y)={\frac {e^{ikr_{+}}}{r_{+}}}+{\frac {e^{ikr_{-}}}{r_{-}}},

where $k=2\pi /\lambda .\!$

(a) Considering just the exponential factors, show that constructive interference appears approximately at

{\frac {y}{r}}=n{\frac {\lambda }{d}}

where $r={\sqrt {x^{2}+y^{2}+L^{2}}}.$

(b) Make a plot of the intensity $\left|\psi (0,y)\right|^{2}$ as a function of $y\!$ , by choosing $k=1,\!$ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d =20,\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=1000.\!} The intensity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\psi(0,y)\right |^{2}} is interpreted as the probability distribution for the electron to be detected on the screen, after repeating the same experiment many many times.

(c) Make a contour plot of the intensity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\psi(x,y)\right |^{2}} as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y\!} , for the same parameters.

(d) If you place a counter at both pinholes to see if the electron has passed one of them, all of a sudden the wave function "collapses". If the electron is observed to pass through the pinhole at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=+d/2\!} , the wave function becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{+}(x,y)=\frac{e^{ikr_{+}}}{r_{+}}.}

If it is observed to pass through that at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=-d/2\!} , the wave function becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{-}(x,y)=\frac{e^{ikr_{-}}}{r_{-}}.}

After repeating this experiment many times with 50:50 probability for each the pinholes, the probability on the screen will be given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\psi_{+}(x,y)\right |^{2}+\left |\psi_{-}(x,y)\right |^{2}\!}

instead. Plot this function on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis, and also show the contour plot, to compare its pattern to the case when you do not place a counter. What is the difference from the case without the counter?

Solution

External Links

Simulation of the Stern-Gerlach Experiment
Another simulation of the Stern-Gerlach Experiment

@@ Line 5: / Line 5: @@
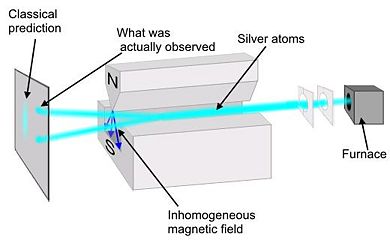
 A collimated monochromatic beam of silver atoms (Ag) is subjected to an inhomogeneous magnetic field. Silver was chosen because it has all of its shells full except for one additional electron in the <math> 5s \!</math> shell. It is necessary to use a non-uniform magnetic field because, if the field was uniform, the trajectory of the silver atoms would be unaffected. In a non-uniform field the force on one end of the dipole is greater than the other.
-Classical theory would predict that there would be a continuous line at the collector plate because the spin would be random valued.
+Classical theory would predict that there would be a continuous line at the collector plate because the orientation of the spin would be completely random.  However, at the collector there was only two spots.  The atoms were deflected in the vertical direction by specific amount equal to <math>\pm \hbar/2</math>, thus showing that spin is quantized. Because there were only two spots at the collector, we conclude that the electron is a spin ½ particle.
-However, at the collector there was only two spots. The atoms were deflected in the vertical direction by specific amount equal to <math>\pm \hbar/2</math>, thus showing that spin is quantized. Because there were only two spots at the collector the electorn is a spin ½ particle.
-It is important to note here that this spin does not arise because the particle is spinning. If this were the case, then it would mean that parts of the spinning electron would be moving faster than the speed of light.
+It is important to note here that this spin does not arise because the particle is spinning.  If this were the case, then it would mean that parts of the spinning electron would be moving faster than the speed of light.
-A sample problem: [http://wiki.physics.fsu.edu/wiki/index.php/Phy5645/Double_pinhole_experiment The double pinhole experiment]<br />
+== History ==
+While our present understanding of the Stern-Gerlach experiment is that it demonstrates the fact that electrons have spin, one must keep in mind that the experiment was performed in 1922, three years before the concept of electronic spin was introduced and four years before modern quantum theory was introduced.  As a matter of fact, the results of this experiment were originally taken as a confirmation of the old quantum theory of Bohr and Sommerfeld.
-== The discovery of spin ==
+Sommerfeld, in the old quantum theory, had predicted the spatial quantization of trajectories and the directional quantization in a magnetic field <math> B\!</math>. He knew that the magnetic moment <math> \mu = \gamma L\!</math>, where the orbital gyromagnetic ratio <math> \gamma=q/2m.\!</math>  Sommerfeld understood the principle of the experiment as soon as 1918. And he expected a lot from it because it would have been the first proof of quantization in a non-radiative process.
-Talking about the Stern-Gerlach experiment, one naturally thinks that they have discovered spin 1/2! They have found the quantization of the magnetic moment, the superposition principle, and the explanation of the electron’s magnetic moment if not its spin.
+One could argue, however, that there should be three spots and not two. Imagine an electron in a circular uniform motion around a proton. The <math>z</math> component of [[angular momentum]] is quantized to integer multiples of <math>\hbar</math>. In a magnetic field, the plane of the trajectory could have three directions corresponding, respectively, to an angular momentum parallel, antiparallel, or perpendicular to the field <math>B\!</math> with <math>L_{z}=\hbar, </math> <math>L_{z}=-\hbar, </math> or <math>L_{z}=0.\! </math>
-It is with that type of reasoning and observations that Fresnel had founded the wave theory of light, in particular the laws of polarization, which was a similar and difficult problem in the 19th century.
+This is not the case - as soon as 1918, Bohr proved that the trajectory for which <math> L_{z}=0 \!</math> was unstable. One must, therefore, only observe two spots, corresponding to <math>L_{z} = \pm \hbar \! </math>.  This is exactly what Stern and Gerlach observed.
-However, this was not the case.  The result was considered as perfectly natural, and as a brilliant confirmation of the old quantum theory of Bohr and Sommerfeld (remember this happened in 1922).
-However, at that time physicists were concerned with quite a different problem: they wanted to prove the old quantum theory and the quantization of trajectories that Bohr had used in his model of the [[hydrogen atom]]<nowiki />. Actually, the Stern–Gerlach experiment had been induced by the theorists Born, Bohr, Sommerfeld, and Pauli for months, if not for years, and they had predicted the result.
+Furthermore, by measuring <math>\mu _{0}\!</math>, they found that, to a few percent, the magnetic moment of an atom was
-In physics it often occurs that one believes in a result only if a theory has predicted it. An example is the discovery of the 3 K cosmic background radiation by Penzias and Wilson. It was considered as a background noise until they were told about the prediction of Gamow of the existence of background radiation in the big bang theory.
+:<math>\mu _{0}=\left | \gamma ^{orb}_{0} \right |\hbar=\frac{q\hbar}{2m_{e}},
+</math>
+as predicted by Bohr and Sommerfeld.  Therefore, it was believed that the experiment had confirmed the old quantum theory.  However, in our modern quantum theory, <math>L_z\!</math> may be zero, which would appear to contradict the results of the Stern-Gerlach experiment.  However, if one accounts for electronic spin, then one will correctly predict two spots.
+==Problem==
+(Double Pinhole Experiment)
+Besides the Stern-Gerlach experiment, the double slit experiment also demonstrates the difference between quantum mechanics and classical mechanics.  However, let us instead consider a double pinhole experiment rather than a double slit experiment because the former is mathematically simpler and still embodies the basic physics that we wish to demonstrate.
+[[Image:Double_pinhole_1.JPG]]
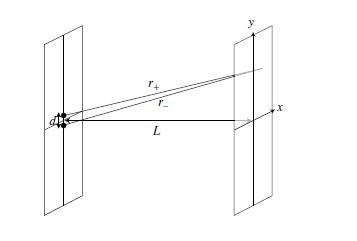
+Suppose that a beam of electrons, traveling along the <math>z\!</math> axis, hits a screen at <math>z = 0\!</math> with two pinholes at <math>x = 0, y = \pm d/2</math>. For a point <math>(x,y)\!</math> on a second screen at <math>z = L>>d, \lambda\!</math>, the distance from each pinhole is given by <math> r_{\pm}=\sqrt{x^{2}+(y\mp d/2)^{2}+L^{2}}.</math>  A spherical wave is emitted from each pinhole; the waves from each add, and the wave function at a given point on the second screen is
+:<math>\psi(x,y)=\frac{e^{ikr_{+}}}{r_{+}}+\frac{e^{ikr_{-}}}{r_{-}},</math>
-The quantization of <math>L_{z}\!</math> had been guessed very early. Sommerfeld, in the old quantum theory, had predicted the spatial quantization of trajectories and the directional quantization in a magnetic field <math> B \!</math>. He knew that <math> \mu = \gamma L \!</math>, and that the orbital gyromagnetic ratio is <math> q/2m \! </math>. Sommerfeld understood the principle of the experiment as soon as 1918. And he expected a lot from it because it would have been the first proof of quantization in a non-radiative process.
+where <math> k = 2\pi /\lambda.\!</math>
-But one could argue that there should be three spots and not two. Imagine an electron in a circular uniform motion around a proton. The quantization of [[angular momentum]] is an integer multiple of <math>\hbar</math>. In a magnetic field, the plane
+'''(a)''' Considering just the exponential factors, show that constructive interference appears approximately at
-of the trajectory could have three directions corresponding, respectively, to an angular momentum parallel, antiparallel, or perpendicular to the field B with <math>L_{z}=\hbar \!</math>, <math>L_{z}=-\hbar \!</math>, or <math>L_{z}=0 \!</math>.
-Not at all! As soon as 1918, Bohr proved that the trajectory <math> L_{z}=0 \!</math> was unstable. One must, therefore, observe only two spots <math>L_{z} = \pm 1 \! </math>.
+:<math> \frac{y}{r}=n\frac{\lambda}{d}</math>
-Born insisted in 1920 (he was 30), “This experiment must absolutely be done.” At that time, Born was a professor in Frankfurt, where there was an artist of atomic and molecular beams, Otto Stern (32 at that time), but Stern wasn’t interested.
-So, Born, who was a mathematician, decided to do experiments. And he managed to do so thanks to a talented assistant named Elizabeth Bormann.
+where <math> r=\sqrt{x^{2}+y^{2}+L^{2}}.</math>
-This new activity of Born was a surprise to all physicists. (One day, Rutherford asked him if he had a relative doing experiments. Born answered, “No, but I have a good assistant.”)
-But Born had to face the facts; he suffered from the Pauli effect: the better you are as a theorist, the more you are a disastrous experimentalist. Whenever Pauli entered a laboratory, everything went wrong. One day, in Gottingen, an experimental setup of Franck exploded. Everyone looked for Pauli, but there was no trace of him. Some time later, someone learned that at the precise time of the explosion, Pauli was on a train, which had stopped in Gottingen,on the way from Munich to Hanover. The Pauli effect acted at a distance!
+'''(b)''' Make a plot of the intensity <math>\left |\psi(0,y)\right |^{2}</math> as a function of <math>y\!</math>, by choosing <math>k=1,\!</math> <math>d =20,\!</math> and <math> L=1000.\!</math>  The intensity <math>\left |\psi(0,y)\right |^{2}</math> is interpreted as the probability distribution for the electron to be detected on the screen, after repeating the same experiment many many times.
-Born eventually convinced Stern. Actually, Stern did not know what to think. At first he proposed the experiment, but some time later he was skeptical, “Quantum restrictions on trajectories are simply calculational rules. I’m going to show once for all that what theorists say is nonsense.” However, Stern suffered somewhat from the Pauli effect. All his experimental setups were constructed by his technician. He knew remarkably how to conceive them, but he wasn’t very skillful.
+'''(c)''' Make a contour plot of the intensity <math>\left |\psi(x,y)\right |^{2}</math> as a function of <math>x\!</math> and <math>y\!</math>, for the same parameters.
-And, then, it was too difficult: neither the technician nor Bormann succeeded. Fortunately, Gerlach, who was a very talented 21-year-old
+'''(d)''' If you place a counter at both pinholes to see if the electron has passed one of them, all of a sudden the wave function "collapses". If the electron is observed to pass through the pinhole at <math>y=+d/2\!</math>, the wave function becomes
-experimentalist, had just arrived in Frankfurt, after graduating in Tubingen.
-Born said “Thank God, now we have at last someone who knows how to do experiments!” Gerlach took care of everything – the technician, Bormann, and Stern’s ideas – and he did the experiment. He was successful, and found the two spots. It seemed to be a triumph for Sommerfeld. Pauli (22 at that time) congratulated Gerlach and said to him: “Let us hope now that the old unbeliever Stern will now be convinced of directional quantization!”
-The triumph was even greater because, by measuring <math>\mu _{0}\!</math> they found to a few percent
+:<math>\psi_{+}(x,y)=\frac{e^{ikr_{+}}}{r_{+}}.</math>
-:<math>\mu _{0}=\left | \gamma ^{orb}_{0} \right |\hbar=\frac{q\hbar}{2m_{e}}
+If it is observed to pass through that at <math>y=-d/2\!</math>, the wave function becomes
-</math>
-exactly the prediction of Bohr and Sommerfeld!
-At that time, nobody could suspect that Nature had played a bad trick. Above equation must be read as
+:<math>\psi_{-}(x,y)=\frac{e^{ikr_{-}}}{r_{-}}.</math>
-:<math>\mu ^{spin}=\left ( \frac{q}{m_{e}} \right )\left ( \frac{\hbar}{2} \right )</math>,
+After repeating this experiment many times with 50:50 probability for each the pinholes, the probability on the screen will be given by
-and not
+:<math>\left |\psi_{+}(x,y)\right |^{2}+\left |\psi_{-}(x,y)\right |^{2}\!</math>
-:<math>\mu ^{spin}=\left ( \frac{q}{2m_{e}} \right )\left ( \hbar \right )</math>
+instead. Plot this function on the <math>y</math>-axis, and also show the contour plot, to compare its pattern to the case when you do not place a counter. What is the difference from the case without the counter?
-In other words, the spin gyromagnetic ratio is twice the orbital gyromagnetic ratio, and the angular momentum is <math>\frac{\hbar}{2}</math>. Dirac proved that in 1927, for any charged pointlike spin 1/2 particle, in his theory of a relativistic electron. Einstein used to say that the Lord is not mean, but he is subtle. On that point, the Lord had really been nasty!
+[[Phy5645/Double_pinhole_experiment|Solution]]
 ==External Links==
 [http://phet.colorado.edu/sims/stern-gerlach/stern-gerlach_en.html Simulation of the Stern-Gerlach Experiment]<br/>
 [http://www.if.ufrgs.br/~betz/quantum/SGPeng.htm Another simulation of the Stern-Gerlach Experiment]

Stern-Gerlach Experiment: Difference between revisions

Latest revision as of 13:36, 8 August 2013

History

Problem

External Links

Navigation menu

Search