Stern-Gerlach Experiment

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian ${\mathcal {H}}$, it describes how a state $|\Psi \rangle$ evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

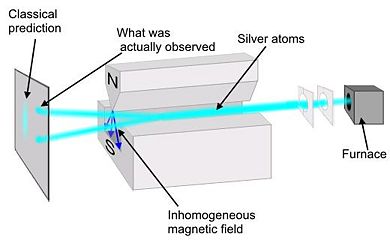
Preformed in 1922 by Walter Stern and Otto Gerlach, this experiment demonstrated that particles have intrinsic spin. A collimated monochromatic beam of silver atoms (Ag) is subjected to an inhomogeneous magnetic field. Silver was chosen because it has all of its shells full except for one additional electron in the $5s\!$ shell. It is necessary to use a non-uniform magnetic field because, if the field was uniform, the trajectory of the silver atoms would be unaffected. In a non-uniform field the force on one end of the dipole is greater than the other.

Classical theory would predict that there would be a continuous line at the collector plate because the spin would be random valued. However, at the collector there was only two spots. The atoms were deflected in the vertical direction by specific amount equal to $\pm \hbar /2$, thus showing that spin is quantized. Because there were only two spots at the collecter the electorn is a spin ½ particle.

It is important to note here that this spin does not arise because the particle is spinning. If this were the case then this would mean that the electron would be spinning faster than the speed of light.

A sample problem: The double pinhole experiment

The discovery of spin

Talking about the Stern-Gerlach experiment, one naturally thinks that they have discovered spin 1/2! They have found the quantization of the magnetic moment, the superposition principle, and the explanation of the electron’s magnetic moment if not its spin.

It is with that type of reasoning and observations that Fresnel had founded the wave theory of light, in particular the laws of polarization, which was a similar and difficult problem in the 19th century. However, this was not the case. The result was considered as perfectly natural, and as a brilliant confirmation of the old quantum theory of Bohr and Sommerfeld (remember this happened in 1922).

However, at that time physicists were concerned with quite a different problem: they wanted to prove the old quantum theory and the quantization of trajectories that Bohr had used in his model of the hydrogen atom. Actually, the Stern–Gerlach experiment had been induced by the theorists Born, Bohr, Sommerfeld, and Pauli for months, if not for years, and they had predicted the result.

In physics it often occurs that one believes in a result only if a theory has predicted it. An example is the discovery of the $3K\!$ cosmic background radiation by Penzias and Wilson. It was considered as a background noise until they were told about the prediction of Gamow of the existence of background radiation in the big bang theory.

The quantization of $L_{z}\!$ had been guessed very early. Sommerfeld, in the old quantum theory, had predicted the spatial quantization of trajectories and the directional quantization in a magnetic field $B\!$. He knew that $\mu =\gamma L\!$, and that the orbital gyromagnetic ratio is $q/2m\!$. Sommerfeld understood the principle of the experiment as soon as 1918. And he expected a lot from it because it would have been the first proof of quantization in a non-radiative process.

But one could argue that there should be three spots and not two. Imagine an electron in a circular uniform motion around a proton. The quantization of angular momentum is an integer multiple of $\hbar$. In a magnetic field, the plane of the trajectory could have three directions corresponding, respectively, to an angular momentum parallel, antiparallel, or perpendicular to the field B with $L_{z}=\hbar \!$, $L_{z}=-\hbar \!$, or $L_{z}=0\!$.

Not at all! As soon as 1918, Bohr proved that the trajectory $L_{z}=0\!$ was unstable. One must, therefore, observe only two spots $L_{z}\pm 1\!$. Born insisted in 1920 (he was 30), “This experiment must absolutely be done.” At that time, Born was a professor in Frankfurt, where there was an artist of atomic and molecular beams, Otto Stern (32 at that time), but Stern wasn’t interested.

So, Born, who was a mathematician, decided to do experiments. And he managed to do so thanks to a talented assistant named Elizabeth Bormann. This new activity of Born was a surprise to all physicists. (One day, Rutherford asked him if he had a relative doing experiments. Born answered, “No, but I have a good assistant.”)

But Born had to face the facts; he suffered from the Pauli effect: the better you are as a theorist, the more you are a disastrous experimentalist. Whenever Pauli entered a laboratory, everything went wrong. One day, in Gottingen, an experimental setup of Franck exploded. Everyone looked for Pauli, but there was no trace of him. Some time later, someone learned that at the precise time of the explosion, Pauli was on a train, which had stopped in Gottingen,on the way from Munich to Hanover. The Pauli effect acted at a distance!

Born eventually convinced Stern. Actually, Stern did not know what to think. At first he proposed the experiment, but some time later he was skeptical, “Quantum restrictions on trajectories are simply calculational rules. I’m going to show once for all that what theorists say is nonsense.” However, Stern suffered somewhat from the Pauli effect. All his experimental setups were constructed by his technician. He knew remarkably how to conceive them, but he wasn’t very skillful.

And, then, it was too difficult: neither the technician nor Bormann succeeded. Fortunately, Gerlach, who was a very talented 21-year-old experimentalist, had just arrived in Frankfurt, after graduating in Tubingen. Born said “Thank God, now we have at last someone who knows how to do experiments!” Gerlach took care of everything – the technician, Bormann, and Stern’s ideas – and he did the experiment. He was successful, and found the two spots. It seemed to be a triumph for Sommerfeld. Pauli (22 at that time) congratulated Gerlach and said to him: “Let us hope now that the old unbeliever Stern will now be convinced of directional quantization!”

The triumph was even greater because, by measuring $\mu _{0}\!$ they found to a few percent

$\mu _{0}=\left|\gamma _{0}^{orb}\right|\hbar ={\frac {q\hbar }{2m_{e}}}$

exactly the prediction of Bohr and Sommerfeld!

At that time, nobody could suspect that Nature had played a bad trick. Above equation must be read as

$\mu ^{spin}=\left({\frac {q}{m_{e}}}\right)\left({\frac {\hbar }{2}}\right)$,

and not

$\mu ^{spin}=\left({\frac {q}{2m_{e}}}\right)\left(\hbar \right)$

In other words, the spin gyromagnetic ratio is twice the orbital gyromagnetic ratio, and the angular momentum is ${\frac {\hbar }{2}}$. Dirac proved that in 1927, for any charged pointlike spin 1/2 particle, in his theory of a relativistic electron. Einstein used to say that the Lord is not mean, but he is subtle. On that point, the Lord had really been nasty!

External Links

Simulation of the Stern-Gerlach Experiment
Another simulation of the Stern-Gerlach Experiment