Stern-Gerlach Experiment

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian ${\mathcal {H}}$, it describes how a state $|\Psi \rangle$ evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

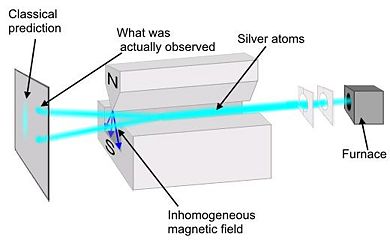
Preformed in 1922 by Walter Stern and Otto Gerlach, this experiment demonstrated that particles have intrinsic spin. A collimated monochromatic beam of silver atoms (Ag) is subjected to an inhomogeneous magnetic field. Silver was chosen because it has all of its shells full except for one additional electron in the $5s\!$ shell. It is necessary to use a non-uniform magnetic field because, if the field was uniform, the trajectory of the silver atoms would be unaffected. In a non-uniform field the force on one end of the dipole is greater than the other.

Classical theory would predict that there would be a continuous line at the collector plate because the orientation of the spin would be completely random. However, at the collector there was only two spots. The atoms were deflected in the vertical direction by specific amount equal to $\pm \hbar /2$, thus showing that spin is quantized. Because there were only two spots at the collector, we conclude that the electron is a spin ½ particle.

It is important to note here that this spin does not arise because the particle is spinning. If this were the case, then it would mean that parts of the spinning electron would be moving faster than the speed of light.

A sample problem: The double pinhole experiment

History

While our present understanding of the Stern-Gerlach experiment is that it demonstrates the fact that electrons have spin, one must keep in mind that the experiment was performed in 1922, three years before the concept of electronic spin was introduced and four years before modern quantum theory was introduced. As a matter of fact, the results of this experiment were originally taken as a confirmation of the old quantum theory of Bohr and Sommerfeld.

Sommerfeld, in the old quantum theory, had predicted the spatial quantization of trajectories and the directional quantization in a magnetic field $B\!$. He knew that $\mu =\gamma L\!$, and that the orbital gyromagnetic ratio is $q/2m\!$. Sommerfeld understood the principle of the experiment as soon as 1918. And he expected a lot from it because it would have been the first proof of quantization in a non-radiative process.

One could argue, however, that there should be three spots and not two. Imagine an electron in a circular uniform motion around a proton. The $z$ component of angular momentum is quantized to integer multiples of $\hbar$. In a magnetic field, the plane of the trajectory could have three directions corresponding, respectively, to an angular momentum parallel, antiparallel, or perpendicular to the field B with $L_{z}=\hbar \!$, $L_{z}=-\hbar \!$, or $L_{z}=0\!$.

This is not the case - as soon as 1918, Bohr proved that the trajectory for which $L_{z}=0\!$ was unstable. One must, therefore, only observe two spots, corresponding to $L_{z}=\pm 1\!$. This is exactly what Stern and Gerlach observed.

Furthermore, by measuring $\mu _{0}\!$, they found that, to a few percent, the magnetic moment of an atom was

$\mu _{0}=\left|\gamma _{0}^{orb}\right|\hbar ={\frac {q\hbar }{2m_{e}}},$

as predicted by Bohr and Sommerfeld. Therefore, it was believed that the experiment had confirmed the old quantum theory. However, in our modern quantum theory, $L_{z}$ may be zero, which would appear to contradict the results of the Stern-Gerlach experiment. However, if one accounts for electronic spin, then one will correctly predict two spots.

External Links

Simulation of the Stern-Gerlach Experiment
Another simulation of the Stern-Gerlach Experiment