Hydrogen Atom

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Illustration of the hydrogen atom.

We now discuss the solution of the Schrödinger equation for the hydrogen atom. We are especially interested in this system because it is of direct physical interest and because it is possible to solve it exactly.

The effective one-dimensional problem for this system is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2\mu}\frac{d^2}{dr^2}+\frac{\hbar^2}{2\mu}\frac{l(l+1)}{r^2}-\frac{Ze^2}{r}\right] u_{nl}=Eu_{nl},}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=1\!} represents the hydrogen atom, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=2\!} represents the helium ion, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle He^+,\!} and so on. Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu\!} is the effective mass of the atom.

We will focus on the bound states here. To solve the above equation, let us begin by writing down its solutions in the limits of small and large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!.}

In the limit of small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r;\!} i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \to 0,} the equation becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2\mu}\frac{d^2}{dr^2}+\frac{\hbar^2}{2\mu}\frac{l(l+1)}{r^2}\right] u_{nl}=0.}

The only solution to this equation that is not divergent as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\to 0} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)\sim r^{l+1}.\!}

In the opposite limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \to \infty,} we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 u_{nl}}{dr^2}+\frac{2\mu E}{\hbar^2}u_{nl}=0.}

The only solution to this equation that does not diverge as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\to\infty} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)\sim e^{-r/a},\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\sqrt{\frac{-\hbar^2}{2\mu E}}.}

Let us now define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=a^{-1}.\!} The above asymptotic limit for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} can now be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)\sim e^{-\kappa r}.\!}

We now assume that the full expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)\!} has the form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)=(\kappa r)^{l+1}e^{-\kappa r}W(\kappa r).\!}

To simplify the equation, let us introduce the dimensionless radial coordinate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\kappa r,\!} so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r)\!} may now be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(\rho)=\rho^{l+1}e^{-\rho}W(\rho).\!}

Substituting this into the effective Schrödinger equation and simplifying, it becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2W}{d\rho^2}+2\left(\frac{l+1}{\rho}-1\right)\frac{dW}{d\rho}+\left(\frac{\rho_0}{\rho}-\frac{2(l+1)}{\rho}\right)W=0,}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{0}=Ze^{2}\sqrt{\frac{2\mu }{\hbar^{2}E}}.}

Let us now try a series solution for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho):\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)=a_0+a_1 \rho+a_2\rho^2+...=\sum_{k=0}^\infty a_k \rho^k}

Our equation now becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^\infty (a_{k}k(k-1)\rho^{k-2}+2(l+1)k\rho^{k-2}a_k-2\rho^{k-1}a_k k)+\sum_{k=0}^\infty(\rho_0 a_k\rho^{k-1}-2(l+1)a_k\rho^{k-1})=0,}

or, upon simplification,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^\infty (a_{k+1}(k+1)k\rho^{k-1}+2(l+1)(k+1)\rho^{k-1}a_{k+1}-2\rho^{k-1}a_k k+(\rho_0-2(l+1))a_k\rho^{k-1})=0.}

Setting the coefficients of all powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\!} to zero, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k(k+1)a_{k+1}+2(l+1)(k+1)a_{k+1}-2ka_k+(\rho_0-2(l+1))a_k=0,\!}

or

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{2(k+l+1)-\rho_0}{(k+1)(k+2l+2)}.}

In the limit of large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k,\!} the recursion relation becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{2}{k},}

or

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{k+1}=\frac{2}{k}a_k=\frac{2^k}{k!}.}

These are the coefficients of the series for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{2\rho}.\!} We therefore see that, unless we terminate the series at a finite order (i.e., we make Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)\!} a polynomial), the wave function will diverge as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\to\infty.} If we wish to terminate the series at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^{\text{th}}\!} order, we set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{N+1}=0.\!} This yields the condition,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0=2(N+l+1).\!}

If we now solve this for the energy, we obtain the energy eigenvalues of the system,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{Nl}=-\frac{Z^2\mu e^4}{2\hbar^2(N+l+1)^2}.}

The recursion relation now becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{2(k-N)}{(k+1)(k+2l+2)}.}

The function, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho),\!} can be expressed in terms of the confluent hypergeometric function,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=1+\frac{a}{c}\frac{z}{1!}+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+...=\sum_{k=0}^\infty a_k z^k,}

which is a solution of Kummer's equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\frac{d^2w}{dz^2} + (b-z)\frac{dw}{dz} - aw = 0.\,\!}

If we assume a power series solution as before, then the recursion relations are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{a+k}{(c+k)(k+1)}.}

Comparing this form to the recursion relations for our solution for $W(\rho ),\!$ we see that

$c=2(l+1),\!$

$a=-N,\!$

and

$z=2\rho .\!$

Therefore, we may write $W(\rho )\!$ as

$W(\rho )=C_{1}F_{1}(-N,2(l+1),2\rho ),\!$

where $\rho =\kappa r={\sqrt {\frac {-2\mu E}{\hbar ^{2}}}}r.$

The full normalized wave function is given by

$\psi _{n,l,m}(r,\theta ,\phi )={\frac {e^{-\kappa r}(2\kappa r)^{l}}{(2l+1)!}}{\sqrt {\frac {(2\kappa )^{3}(n+l)!}{2n(n-l+1)}}}\ _{1}F_{1}(-n+l+1,2(l+1),2\kappa r)Y_{l}^{m}(\theta ,\phi ),$

where we have introduced the more commonly-used principal quantum number $n=N+l+1.\!$

The first few normalized wave functions for the hydrogen atom are as follows

$\psi _{100}={\dfrac {e^{-r/a}}{\sqrt {\pi a^{3}}}}$

$\psi _{200}={\dfrac {e^{-r/2a}}{\sqrt {32\pi a^{3}}}}\left(2-{\dfrac {r}{a}}\right)$

$\psi _{210}={\dfrac {e^{-r/2a}}{\sqrt {32\pi a^{3}}}}\left({\dfrac {r}{a}}\right)\cos(\theta )$

$\psi _{2\pm 10}={\dfrac {e^{-r/2a}}{\sqrt {64\pi a^{3}}}}\left({\dfrac {r}{a}}\right)\sin(\theta )e^{\pm i\phi }$

The energy may be written as

$E=-{\frac {Z^{2}\mu e^{4}}{2\hbar ^{2}n^{2}}}=-{\frac {Z^{2}}{n^{2}}}\,{\text{Ry}},$

where the Rydberg ${\text{Ry}}=13.6\,{\text{eV}}\!$ for the hydrogen atom and $n=1,2,3,...\!$ The degeneracy of each energy level is $n^{2}.\!$

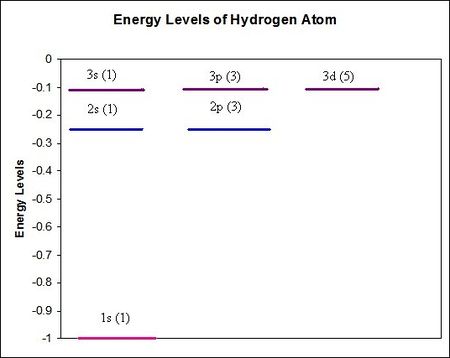
To the side is a chart that depicts the energy levels for the hydrogen atom graphically for $n=1,2,3\!$ in units of ${\text{Ry}}\!$. The parenthesis indicates the degeneracy due to possibile values of the magnetic quantum number $m$ from $-l$ to $+l.$

Problems

(1)

This problem taken from Quantum Mechanics: Concepts and Applications by Nouredine Zettili: Exercise 6.3

An electron in a hydrogen atom is in the energy eigenstate $\psi _{2,1,1}\left(r,\theta ,\phi \right)=Nre^{-{\frac {r}{2a_{o}}}}Y_{1,-1}\left(\theta ,\phi \right)$. (a) Find the normalization constant, N.

Solution

Problem 2