Feynman Path Integrals

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian ${\mathcal {H}}$, it describes how a state $|\Psi \rangle$ evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

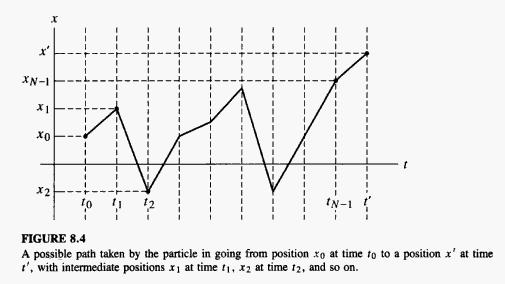
The path integral formulation was developed in 1948 by Richard Feynman. The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique trajectory for a system with a sum, or functional integral, over an infinity of possible trajectories to compute a quantum amplitude.

The classical path is the path that minimizes the action.

The formulation has proved crucial to the subsequent development of theoretical physics, since it is apparantly symmetric between time and space. Unlike previous methods, the path-integral offers physicist an easily method to change coordinates between very different canonical descriptions of the same quantum system.

For simplicity, the formalism is developed here in one dimension.

Using the path integral method, the propagator, $U(t)$, is found directly. The amplitude for a particle to start at $x_{0}$ at $t=0$ and end at $x$ at t can be expressed as a path integral

$\langle x|{\hat {U}}(t)|x_{0}\rangle =\int _{x_{0}}^{x}Dx(t')e^{iS[x(t')]}$

Where $S[x(t)]\!$ is the action for the the path $x(t')$.

The action is given by the time integral of the Lagrangian, just as in classical mechanics $S[x(t')]=\int _{0}^{t}dt'{\mathcal {L}}[x(t'),{\dot {x}}(t'),t']$

Where ${\mathcal {L}}[x(t'),{\dot {x}}(t'),t']={\frac {1}{2}}m{\dot {x}}^{2}(t')-V(x(t'),t')$ is the Lagrangian. Knowing the propagator, we can calculate the probability that a particle in state $x_{0}\!$ at t=0 will be in state $x\!$ at time t by taking the absolute value squared.

Question: Is the Feynman path integral formulation of quantum mechanics is equivalent to Schrödinger equation of motion?

Answer: The path integral reproduces the Schrödinger equation for the initial and final state even when a potential is present. This is easiest to see by taking a path-integral over infinitesimally separated times.

$\psi (y;t+\epsilon )=\int _{-\infty }^{\infty }dx\;\;\psi (x;t)\int _{x(t)=x}^{x(t+\epsilon )=y}e^{{\rm {i}}\int _{t}^{t+\epsilon }({\dot {x}}^{2}-V(x))dt}Dx(t)\qquad (1)$

Since the time separation is infinitesimal and the cancelling oscillations become severe for large values of $\scriptstyle {\dot {x}}$, the path integral has most weight for y close to x. In this case, to lowest order the potential energy is constant, and only the kinetic energy contribution is nontrivial. The exponential of the action is

$e^{-{\rm {i}}\epsilon V(x)}e^{{\rm {i}}{\dot {x}}^{2}\epsilon }\,$

The first term rotates the phase of $\psi (x)$ locally by an amount proportional to the potential energy. The second term is the free particle propagator, corresponding to i times a diffusion process. To lowest order in $\epsilon$ they are additive; in any case one has with (1):

$\psi (y;t+\epsilon )\approx \int \psi (x;t)e^{-{\rm {i}}\epsilon V(x)}e^{{\rm {i}}(x-y)^{2} \over 2\epsilon }dx\,.$

As mentioned, the spread in $\psi$ is diffusive from the free particle propagation, with an extra infinitesimal rotation in phase which slowly varies from point to point from the potential:

${\frac {\partial \psi }{\partial t}}={\rm {i}}\cdot \{{\frac {1}{2}}\nabla ^{2}-V(x)\}\psi \,$

and this is the Schrödinger equation. Note that the normalization of the path integral needs to be fixed in exactly the same way as in the free particle case. An arbitrary continuous potential does not affect the normalization, although singular potentials require careful treatment.

Question: The Feynman path integral formulation of quantum mechanics is more complex than solving the Schrödinger equation to get the dynamics of a quantum particle, why this formulation is mentioned in the text books and where it may be useful?

Answer: As far as a single particle is concerned it is recommended to use Schrödinger equation of motion. However, to study a many particle system getting dynamics by means of Schrödinger equation is quite complicated and messy (let say sometimes impossible), while the Feynman path integral is a good tool for dealing with many particle problems by defining the field operators. More importantly, the generalization of quantum mechanics to relativistic problem can be done in terms of field theory via Feynman path integral formulation.

Explicit evaluation of the path integral for the harmonic oscillator can be found here File:FeynmanHibbs H O Amplitude.pdf