Feynman Path Integrals

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

The path integral formulation of quantum mechanics was developed in 1948 by Richard Feynman. The path integral formulation is a description of quantum theory that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique trajectory for a system with a sum, or functional integral, over an infinity of possible trajectories to compute a quantum amplitude.

The classical path is the path that minimizes the action.

This formulation has proved crucial to the subsequent development of theoretical physics, since it is apparently symmetric between time and space. Unlike previous methods, the path-integral offers us an easily method by which we may change coordinates between very different canonical descriptions of the same quantum system.

For simplicity, the formalism is developed here in one dimension.

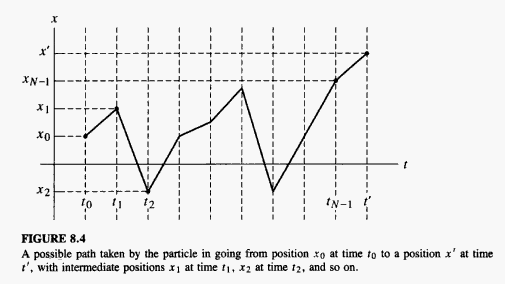
In the path integral formalism, we start by writing the amplitude for a particle at position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i\!} at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_i\!} to move to a position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_f\!} at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_f\!} as a path integral. This path integral is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(x_f,t_f;x_i,t_i)=\langle x_f,t_f|\hat{U}(t_f,t_i)|x_i,t_i\rangle=\int D x(t')\,e^{iS[x(t')]/\hbar}, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[x(t)]\!} is the action for the the path Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t')\!} and the integral is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int D x(t')=\lim_{N\to\infty}\left (\frac{m}{2\pi i\hbar\,\delta t}\right )^{N/2}\left (\prod_{j=1}^{N-1}\int_{-\infty}^{\infty} dx_j\right ),}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\!} is a number of "slices" of length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\!} that we divide the time axis up into. Essentially, we define the path integral as a limit of an integral over all possible values of the particle's intermediate positions on its path from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x.\!}

The action is given by the time integral of the Lagrangian, just as in classical mechanics: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[x(t')]=\int_{t_i}^{t_f} dt' \mathcal{L}[x(t'),\dot{x}(t'),t'], }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}[x(t'),\dot{x}(t'),t']=\tfrac{1}{2}m\dot{x}^2(t')-V(x(t'),t') }

is the Lagrangian.

Our choice of notation for this path integral, $K(x_{f},t_{f};x_{i},t_{i}),\!$ is motivated by the fact that it serves as a "kernel" for an integral giving the wave function $\Psi (x_{f},t_{f})\!$ in terms of $\Psi (x,t).\!$ This integral is

$\Psi (x_{f},t_{f})=\int _{-\infty }^{\infty }dx\,K(x_{f},t_{f};x,t)\Psi (x,t).$

As a justification of this method, we will show that it reproduces the Schrödinger equation. We will use the method used by Feynman. Let us begin by assuming that the elapsed time $t\!$ is so small, that we may approximate the path integral with a single "time slice" of length $\delta t.\!$ In this case, the kernel is just $e^{iS/\hbar },$ and the action is just its average over the time interval times is length:

$S={\frac {m(x_{f}-x)^{2}}{2\delta t}}-V[{\tfrac {1}{2}}(x_{f}+x),t]\,\delta t$

The kernel now becomes

$K(x_{f},t_{f};x,t)={\sqrt {\frac {m}{2\pi i\hbar \,\delta t}}}\exp \left[{\frac {im(x_{f}-x)^{2}}{2\hbar \,\delta t}}\right]\exp \left[-{\frac {i}{\hbar }}V[{\tfrac {1}{2}}(x_{f}+x),t]\,\delta t\right],$

so that the wave function $\Psi (x_{f},t_{f})=\Psi (x_{f},t+\delta t)\!$ is

$\Psi (x_{f},t+\delta t)={\sqrt {\frac {m}{2\pi i\hbar \,\delta t}}}\int _{-\infty }^{\infty }dx\,\exp \left[{\frac {im(x_{f}-x)^{2}}{2\hbar \,\delta t}}\right]\exp \left[-{\frac {i}{\hbar }}V[{\tfrac {1}{2}}(x_{f}+x),t]\,\delta t\right]\Psi (x,t).$

Now we introduce the variable, $\xi =x_{f}-x,\!$ so that the integral becomes

$\Psi (x_{f},t+\delta t)={\sqrt {\frac {m}{2\pi i\hbar \,\delta t}}}\int _{-\infty }^{\infty }d\xi \,\exp \left({\frac {im\xi ^{2}}{2\hbar \,\delta t}}\right)\exp \left[-{\frac {i}{\hbar }}V(x_{f}-{\tfrac {1}{2}}\xi ,t)\,\delta t\right]\Psi (x_{f}-\xi ,t).$

We now expand the wave function in the integral in powers of $\xi \!$ up to second order and the factor involving the potential in powers of $\delta t\!$ up to first order. We also drop all dependence of the potential on $\xi .\!$ The result of this is

$\Psi (x_{f},t+\delta t)={\sqrt {\frac {m}{2\pi i\hbar \,\delta t}}}\int _{-\infty }^{\infty }d\xi \,\exp \left({\frac {im\xi ^{2}}{2\hbar \,\delta t}}\right)\left[1-{\frac {i}{\hbar }}V(x_{f},t)\,\delta t\right]\left[\Psi (x_{f},t)-{\frac {\partial \Psi (x_{f},t)}{\partial x_{f}}}\xi +{\tfrac {1}{2}}{\frac {\partial ^{2}\Psi (x_{f},t)}{\partial x_{f}^{2}}}\xi ^{2}\right].$

The problem has been reduced to the evaluation of Gaussian integrals. Using the formulas,

$\int _{-\infty }^{\infty }dx\,e^{-ax^{2}}={\sqrt {\frac {\pi }{a}}},$

$\int _{-\infty }^{\infty }dx\,xe^{-ax^{2}}=0,$

and

$\int _{-\infty }^{\infty }dx\,x^{2}e^{-ax^{2}}={\frac {1}{2a}}{\sqrt {\frac {\pi }{a}}},$

we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\left [1-\frac{i}{\hbar}V(x_f,t)\,\delta t\right ]\left [\Psi(x_f,t)+\frac{i\hbar}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}\,\delta t\right ].}

We now multiply out the right-hand side and retain only terms that are first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t.\!} This gives us

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\Psi(x_f,t)+\frac{i\hbar}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}\,\delta t-\frac{i}{\hbar}V(x_f,t)\Psi(x_f,t)\,\delta t.}

Rearranging, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\Psi(x_f,t+\delta t)-\Psi(x_f,t)}{\delta t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}+}V(x_f,t)\Psi(x_f,t).}

Finally, taking the limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\to 0,\!} and renaming Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_f\!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,\!} we finally arrive at the familiar Schrödinger equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial\Psi(x,t)}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi(x,t)}{\partial x^2}+}V(x,t)\Psi(x,t).}

Question: The Feynman path integral formulation of quantum mechanics is more complex than solving the Schrödinger equation to get the dynamics of a quantum particle, why this formulation is mentioned in the text books and where it may be useful?

Answer: As far as a single particle is concerned it is recommended to use Schrödinger equation of motion. However, to study a many particle system getting dynamics by means of Schrödinger equation is quite complicated and messy (let say sometimes impossible), while the Feynman path integral is a good tool for dealing with many particle problems by defining the field operators. More importantly, the generalization of quantum mechanics to relativistic problem can be done in terms of field theory via Feynman path integral formulation.

Explicit evaluation of the path integral for the harmonic oscillator can be found here File:FeynmanHibbs H O Amplitude.pdf