Angular Momentum as a Generator of Rotations in 3D

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian ${\mathcal {H}}$, it describes how a state $|\Psi \rangle$ evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Let us consider an infinitesimal rotation $\mathbf {\alpha } \!$ directed along the axis about which the rotation takes place.We then have

$\mathbf {w} '=\mathbf {w} +\mathbf {\alpha } \times \mathbf {w} =\mathbf {w} +\delta \mathbf {w}$

The changes $\delta \mathbf {w}$ (in the radial vector $\mathbf {w} \!$ of the particle) due to such a rotation is:

$\delta \mathbf {w} =\mathbf {\alpha } \times \mathbf {w}$

so

$\psi \left(\mathbf {w} +\mathbf {\delta } \mathbf {w} \right)=\left(1+\mathbf {\alpha } \cdot \left(\mathbf {w} \times \mathbf {\nabla } \right)\right)\psi \left(\mathbf {w} \right)$

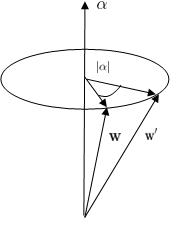
The expression

$1+\mathbf {\alpha } \cdot (\mathbf {w} \times \mathbf {\nabla } )$

is the operator of an infinitesimally small rotation. We recognize the equation

$\mathbf {w} \times \mathbf {\nabla } ={\frac {i}{\hbar }}\mathbf {L}$

Therefore, the infinitesimal rotation operator is

$\mathbf {R} _{inf}=1+{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L}$

This expression is only until the first order correction. The actual rotation operator is calculated by applying this operator N times where N goes to infinity. Doing so, we get the rotation operator for finite angle

$\mathbf {R} =e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }$

In this form, we recognize that angular momentum is the generator of rotation. And we can write the equation relating the initial vector before rotation with the transformed vector as

$\mathbf {w} '=e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }\mathbf {w} e^{-{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }$

This expression of the rotation operator is also valid when the rotation angle is not infinitesimal. What's more, this equation also implies that if we have a scalar instead of $\mathbf {w} \!$, it would be invariant. We can also calculate the effect of the unitary operator $e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }$ on the states:

$\langle r_{0}|e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }\mathbf {\hat {\mathbf {r} }} e^{-{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }=\langle r_{0}|{\hat {\mathbf {r'} }}=r_{0}'\langle r_{0}|$

$\Rightarrow \psi '(r_{0})=\langle r_{0}|\psi '\rangle =\langle r_{0}|e^{{\frac {i}{\hbar }}\mathbf {\alpha } \cdot \mathbf {L} }|\psi \rangle =\langle r_{0}'|\psi \rangle =\psi (r_{0}')$

This is the wavefunction evaluated at a rotated point.

A sample problem