Hydrogen Atom
The Schrödinger equation for the particle moving in central potential can be represented in a spherical coordinate system as follows:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( -\frac{\hbar^2}{2\mu}\frac{1}{r}\frac{\partial^2}{\partial r^2}r+\frac{L^2}{2\mu r^2}+V(r)\right) \psi(r,\theta,\phi)=E\psi(r,\theta,\phi)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L\!} is the angular momentum operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu\!} is the reduced mass.
In this case, being invariant under the rotation, the Hamiltonian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\!} , commutes with both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} . Furthermore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} commute with each other. Therefore, the energy eigenstates can be chosen to be simultaneously the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} . Such states can be expressed as the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,\theta,\phi)=R(r)Y_{lm}(\theta,\phi)=\frac{u_l(r)}{r}Y_{lm}(\theta,\phi)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_l^m(\theta,\phi)} is the spherical harmonic, which is the simultaneous eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} , and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{u_l(r)}{r}} substitution is made for simplification.
Substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,\theta,\phi)=\frac{u_l(r)}{r}Y_{lm}(\theta,\phi) } into the Schrödinger equation, and taking into account the fact that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\psi(r,\theta,\phi)=L^2[R(r)Y_{lm}(\theta,\phi)]=R(r)L^2Y_{lm}(\theta,\phi)=R(r)\hbar^2l(l+1)Y_{lm}(\theta,\phi) =\hbar^2l(l+1)\psi(r,\theta,\phi)}
we have the equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}+V(r)\right] u_l(r)=Eu_l(r)}
In the hydrogen atom or single electron ion, the potential is the Coulomb potential between the electron and the nucleus:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=-\frac{Ze^2}{r}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=1\!} for the hydrogen, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=2\!} for helium ion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle He^+\!} , etc.
Plugging this potential into the Schrödinger equation we obtain
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}-\frac{Ze^2}{r}\right] u_l(r)=Eu_l(r)}
Since we are only concentrating on the bound states, we can write down the solutions to this equation in the asymptotic limits.
In the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \to 0 } limit the equation becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right] u_l(r)=0}
and the solution in this limit is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\rightarrow r^{l+1}} .
In the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \to \infty } limit the equation becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 u_l(r)}{\partial r^2}+\frac{2mE}{\hbar^2}u_l(r)=0}
and the solution in this limit is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\rightarrow e^{-\frac{r}{a}}} .
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\sqrt{\frac{-\hbar^2}{2m E}}}
If we allow Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=a^{-1}\!} , then the large limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} can be expressed as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\sim e^{-\kappa r}\!}
Using the limits of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(r)\!} , the wavefunction can be expressed as the following
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)=(\kappa r)^{l+1}e^{-\kappa r}W(\kappa r)\!}
To simplify the equation, make a substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\kappa r\!} . The equation now turns into
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(\rho)=\rho^{l+1}e^{-\rho}W(\rho)\!}
Plugging this equation into the Schrödinger equation and simplifying, it turns into
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2W(\rho)}{d\rho^2}+2\left(\frac{l+1}{\rho}-1\right)\frac{dW(\rho)}{d\rho}+\left(\frac{\rho_0}{\rho}-\frac{2(l+1)}{\rho}\right)W(\rho)=0} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _{0}=Ze^{2}\sqrt {\frac{2\mu }{\hbar ^{2}E}} }
Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)\!} can be expressed as an expansion of polynomials;
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)=a_0+a_1 \rho+a_2\rho^2+...=\sum_{k=0}^\infty a_k \rho^k}
The Schrödinger equation is then expressed as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^\infty (a_{k}k(k-1)\rho^{k-2}+2(l+1)k\rho^{k-2}a_k-2\rho^{k-1}a_k k)+\sum_{k=0}^\infty(\rho_0 a_k\rho^{k-1}-2(l+1)a_k\rho^{k-1})=0}
And simplified into
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^\infty (a_{k+1}(k+1)k\rho^{k-1}+2(l+1)(k+1)\rho^{k-1}a_{k+1}-2\rho^{k-1}a_k k+(\rho_0-2(l+1))a_k\rho^{k-1})=0}
Bring all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\!} 's to the same power
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k(k+1)a_{k+1}+2(l+1)(k+1)a_{k+1}-2ka_k+(\rho_0-2(l+1))a_k=0\!}
which can be expressed in the simplest fractional form as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{2(k+l+1)-\rho_0}{(k+1)(k+2l+2)}}
where and and
In the limit of large k
this will make
so we need to break, and make
from this, we get the energy spectrum.
The fractional form can be expressed as a confluent hypergeometric function
It should be noted that a confluent hypergeometric function is a solution of Kummer's equation, which is:
Derriving the recursion relations we have:
by comparison, we find that
So the solution of is
where : Full wavefunction solution with normalization is
The first couple of normalized wavefunctions for the hydrogen atom are as follows
The energy is then found to be
where for the hydrogen atom and and the degeneracy for each level is .
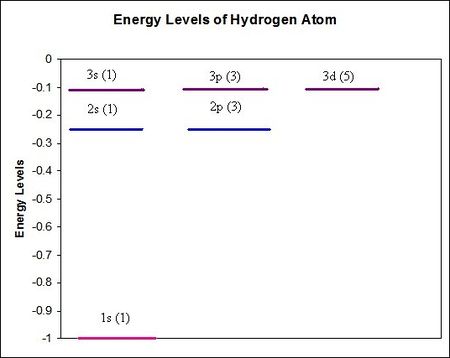
To the side is a chart depicting the energy levels for hydrogen atom for in units of . (The parenthesis indicates the degeneracy due to possibile values of the magnetic quantum number from to ).