Coulomb Potential Scattering

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Example 1

Comparison the differential cross sections for various potential type
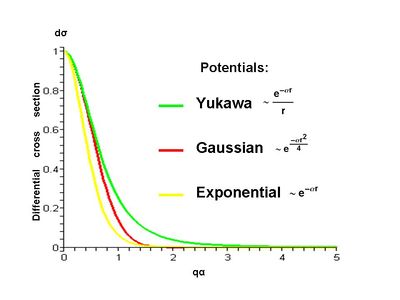
Here we compare the differential cross sections for the Yukawa, Gaussian and exponential potential. We can see that for small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\alpha \!} all differential cross sections are similar. The differential cross section of the exponential potential decreases faster than the others and that of the Yukawa potential decreases little bit slower than the others.

Let's look at an example of a Screened Coulomb (Yukawa) Potential, where we have a potential:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V_0e^{-\alpha r}\frac{1}{r}}

The scattering amplitude can be written by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f &= -\frac{m}{2\pi\hbar^2}\int_0^\infty dr' r'^2 2\pi\frac{e^{-i|\mathbf{k}'-\mathbf{k}|r'}-e^{i|\mathbf{k}-\mathbf{k}'|r'}}{-i|\mathbf{k}'-\mathbf{k}|r'}\frac{V_0e^{-\alpha r'}}{r'} \\ &= -\frac{2mV_0}{\hbar^2}\int_0^\infty dr' r'^2 \frac{\sin\left(|\mathbf{k}'-\mathbf{k}|r'\right)}{|\mathbf{k}'-\mathbf{k}|r'}\frac{e^{-\alpha r'}}{r'} \\ &= -\frac{2mV_0}{\hbar^2}\frac{1}{\left(\left|\mathbf{k}'-\mathbf{k}\right|\right)^2+\alpha^2} \end{align} }

For the elastic scattering Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left| \mathbf{k} \right| = \left| \mathbf{k'} \right| = k \!} . Therefore,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\left|\mathbf{k}'-\mathbf{k}\right|)^2 = 2k\sin\frac{\theta}{2} }

Thus, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = -\frac{2mV_0}{\hbar^2}\frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2} }

thus we have the differential cross section:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}= \left( \frac{2mV_0}{\hbar^2} \right) ^2 \left( \frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}\right) ^2}

Example 2

Parabolic coordinates
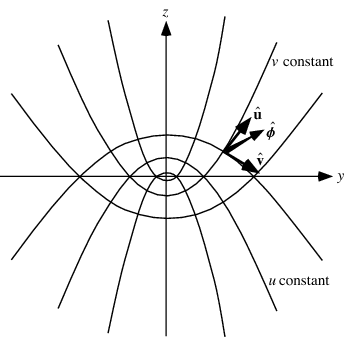
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} represents rotation about the z-axis, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} represents the parabolas with their vertex at a minimum, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\!} represents parabolas with their vertex at a maximum.

When we are considering scattering due to the Coulomb potential, we can not neglect the effect of this potential at large distances because it is only a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r}} potential.

Use a change of coordinates from Cartesian to parabolic coordinates:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=\sqrt{x^2+y^2+z^2}-z}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta=\sqrt{x^2+y^2+z^2}+z}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\tan^{-1}(\frac{y}{x})}

So now we can write the Schrödinger equation in parabolic coordinates:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ - \frac{\hbar^2}{2\mu}\frac{4}{\xi+\eta} \left( \frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{\xi+\eta}{4\xi\eta}\frac{\partial^2}{\partial \phi^2} \right) -\frac{2Ze^2}{\xi+\eta} \right] \psi=\frac{\hbar^2k^2}{2\mu}\psi}

So we will seek solutions which are independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} . Recall that the scattering amplitude is a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} only.

Look for solution of the form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi=e^{\frac{i}{2}k(\eta-\xi)}\Phi(\xi)=e^{ikz}\Phi(r-z)}

Then the equation becomes:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \xi\frac{\partial^2}{\partial \xi^2}+(1-ik\xi)\frac{\partial}{\partial \xi}+\frac{Ze^2\mu}{k\hbar^2}k \right]\Phi(\xi)=0}

We can tidy up the notation a little bit by using the following substitution:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{Ze^2\mu}{k\hbar^2}}

Now let:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=\sum_{n=0}^\infty a_n \xi^n}

From this we can write:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{n+1}}{a_{n}}=\frac{in-\lambda}{(n+1)^2}k=\frac{n+i\lambda}{(n+1)^2}ik}

Recall the confluent hypergeometric function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=1+\frac{a}{c}z+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\dots+\frac{a(a+1)\dots(a+n-1)}{c(c+1)\dots(c+n-1)}\frac{z^n}{n!}+\dots}

We can then write the recursion formula as the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\alpha_{n+1}}{\alpha_n}= \left( \dfrac{a+n}{c+n} \right) \dfrac{1}{n+1}}

This implies that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=A_1F_1(i\lambda,1,ik\xi)\!}

where the confluent geometric function is written in terms of three new variables, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1\!} is a c-number.

Now we can write the wavefunction due to Coulomb scattering:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,z)=A_1F_1(i\lambda,1,ik(r-z))e^{ikz}\!}

Now we should look at the limit where z is taken to go to infinity, and our confluent hypergeometric function is rewritten as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=\frac{\Gamma(c)(-z)^a}{\Gamma(c-a)} \left[ 1-\frac{a(a-c+1)}{z} \right] +\frac{\Gamma(c)}{\Gamma(a)}e^zz^{a-c}}

Now we can use this to rewrite our equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi\!} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=Ae^{\frac{-\pi}{2}\lambda} \left[ \frac{e^{i\lambda \ln(k\xi)}}{\Gamma(1-i\lambda)} \left( 1-\frac{\lambda^2}{ik\xi} \right) +\frac{i\lambda}{ik\xi}\frac{e^{ik\xi+i\lambda \ln(k\xi)}}{\Gamma(1+i\lambda)} \right] }

Rewriting our wavefunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\!} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,\theta)=\frac{Ce^{\frac{-\pi\lambda}{2}}}{\Gamma(1-i\lambda)} \left[ \left( 1-\frac{\lambda^2}{2ikr}\frac{1}{\sin^2\frac{\theta}{2}} \right) e^{ikz}e^{i\lambda \ln(k(r-z))}+\frac{f(\theta)}{r}e^{ikr+i\lambda \ln(2kr)} \right] }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\!} is the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)}\frac{1}{\sin^2\frac{\theta}{2}}e^{i\lambda \ln(\sin^2\frac{\theta}{2})}=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)} \left( \sin^2\frac{\theta}{2} \right) ^{i\lambda-1}}

We can then get our differential cross section from that by squaring it:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f(\theta)|^2=\frac{\lambda^2}{4k^2\sin^4(\frac{\theta}{2})}=\frac{(Ze^2)^2}{16E^2}\frac{1}{\sin^4(\frac{\theta}{2})}}

If we normalize the wavefunction to give unit flux at large distances, we must take the following for the constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\!} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\sqrt{\frac{\mu}{\hbar k}}\Gamma(1-i\lambda)e^{\frac{\pi\lambda}{2}}}

So the wavefunction at large distances is given by the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=|C|^2=\frac{\mu}{\hbar k}|\Gamma(1-i\lambda)|^2e^{\pi\lambda}}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Gamma(1-i\lambda)|^2=\frac{2\pi|\lambda|e^{-\pi\lambda}}{e^{2\pi\lambda}-1}}

Plugging this in for our wavefunction squared:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi|\lambda|}{\frac{\hbar k}{\mu}|1-e^{2\pi\lambda}|}}

Now let's use the following quantity to represent the velocity:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar k}{\mu}=v}

For small incident velocities, we can write:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}e^{-\frac{2\pi Ze^2}{\hbar v}}}

where the first equation is for an attractive Coulomb potential, and the second equation is for a repulsive Coulomb potential.

The factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G \equiv \frac{\pi Ze^2}{\hbar v} \! } , the exponent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-2\frac{\pi Ze^2}{\hbar v}} \!} , is known as the Gamow factor. The Gamow Factor or Gamow-Sommerfeld Factor, named after its discoverer George Gamow, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions. For example, nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier, but when George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.

The Gamow factor for the Coulomb potential can also be obtained via the WKB method. Recall that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \equiv e^{\frac{1}{\hbar} \int_a^b |p(x')|dx'} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(x')=\sqrt{\frac{2m}{\hbar^2}(E-V(x'))}}

For a broad and high barrier, $\theta \gg 1$, and

$T\approx {\frac {1}{\theta ^{2}}}$.

In this case $\theta =e^{{\frac {1}{\hbar }}\int _{-a}^{0}|p(x')|dx'}$

Using our previous potential $V(x')={\frac {Ze^{2}}{|x'|}}$ and $E={\frac {Ze^{2}}{a}}$ we get

$\int _{a}^{b}|p(x')|dx'=\int _{-a}^{0}{\sqrt {{\frac {2m}{\hbar ^{2}}}(|E|-{\frac {Ze^{2}}{|x'|}})}}dx'={\frac {2mE}{\hbar }}\int _{-a}^{0}{\sqrt {|1-{\frac {a}{x'}}|}}dx'$

$=>{\frac {\sqrt {2mE}}{\hbar }}a\int _{0}^{1}{\sqrt {{\frac {1}{u}}-1}}du={\frac {\sqrt {2mE}}{\hbar }}a{\frac {\pi }{2}}={\frac {\sqrt {2m}}{\hbar }}{\frac {Ze^{2}{\sqrt {E}}}{E}}{\frac {\pi }{2}}$

$={\frac {\sqrt {2m}}{\hbar }}{\frac {\pi }{2}}{\frac {Ze^{2}}{\sqrt {E}}}={\frac {\sqrt {2m}}{\hbar }}{\frac {\pi }{2}}{\frac {Ze^{2}}{\sqrt {{\frac {1}{2}}mv^{2}}}}=\pi {\frac {Ze^{2}}{{\hbar }v}}$

So, as above, the transmission coefficient for small v is

$T\approx e^{{\frac {-2\pi }{\hbar }}{\frac {Ze^{2}}{v}}}$