Motion in a Periodic Potential

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

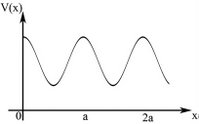
We will now consider the motion of electrons in periodic potentials. An example of such a potential is given in Figure 1.

Figure 1: An example of a periodic potential.

A periodic potential is, by definition, translationally symmetric over a certain period (in Figure 1 it is over period of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} ); i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=V(x + a).\!}

In this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} is the period.

Bloch's Theorem

The Hamiltonian of a system with a periodic potential of period Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!} commutes with translations by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\!:}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T}_a\psi(x)=\psi(x+a)\!}

It is therefore possible to simultaneously diagonalize both the Hamiltonian and the translation operator. We will now show that the eigenfunctions of the Schrödinger equation for this system,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right ]\psi(x)=E\psi(x),}

have the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=e^{ikx}u_k(x)\!}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(x+a)=u_k(x)\!}

has the same period as the potential; this result is known as Bloch's Theorem, and the eigenfunctions are called Bloch waves. To show this, we will prove that eigenfunctions of the translation operator, and thus of the Hamiltonian, have the above form. Applying the translation operator to the proposed wave function, we find that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi(x+a)&=\hat{T}_a\psi(x) \\ &=\hat{T}_a\left (e^{ikx}u_k(x)\right ) \\ &=\left (e^{ik(x+a)}u_k(x+a)\right ) \\ &=e^{ika}\left (e^{ikx}u_k(x)\right ) \\ &=e^{ika}\psi(x) \end{align}}

We see that the proposed wave function is indeed an eigenfunction of the translation operator, with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ika}.\!} The quantity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar k,\!} is sometimes referred to as the crystal momentum, since it is a momentum-like quantity that characterizes the eigenstates of a system with discrete, rather than continuous, translational symmetry.

Also note that, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is complex, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\!} will diverge for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow\pm\infty,} with the choice of sign depending on the sign of the imaginary part of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.\!} Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \!} has to be real if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)\!} is to be a normalizable wave function.

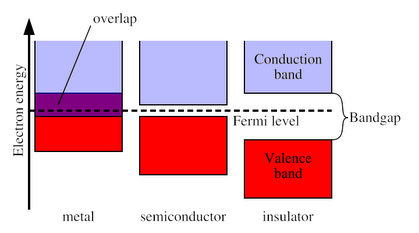
Applying Bloch's Theorem to the Schrödinger equation for a given periodic potential will reveal interesting and important results, such as a "band" structure to the energy spectrum as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!.} For materials with weak electron-electron interactions, one can then deduce, given the Fermi energy of the system, whether such a system is metallic (overlapping bands), semiconducting (small gap between bands), or insulating (large gap between bands) (see Figure 2).

Figure 2. Energy band illustration showing the condition for metal, semiconductor, and insulator.

Dirac Comb Potential

As a simple example, let us consider a Dirac comb potential and the resulting Schrödinger equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=V_0\sum_{n=-\infty}^{\infty}\delta(x-na)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\right)\psi(x)=E\psi(x)}

Let us focus on the region,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < x < a,\!} since the wave function for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\!} may be obtained using Bloch's Theorem. Within this region, the equation simply reduces to that of a free particle, and thus the solution is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi(x) &= Ae^{iqx}+Be^{-iqx} \\ &= e^{ikx}\left(Ae^{i(q-k)x}+Be^{-i(q+k)x}\right) \\ &= e^{ikx}u_k(x) \end{align} }

with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\frac{\hbar^2q^2}{2m}.}

From periodicity and continuity with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \rightarrow 0 } ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(0 - \epsilon)=u_k(0 + \epsilon) = u_k(a + \epsilon)\!}

Thus, the wavefunction from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x < 0 \!} (left) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x > 0 \! } (right) can be written as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_r=e^{ikx}u_k(x)=e^{ikx}(Ae^{i(q-k)x}+Be^{-i(q+k)x})\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_r=e^{ikx}u_k(x+a)=e^{ikx}(Ae^{i(q-k)(x+a)}+Be^{-i(q+k)(x+a)})\!}

When the continuity requirement at x = 0 is also being imposed, the following relation is found:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_l(0)=\psi_r(0)\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A+B=Ae^{i(q-k)a}+Be^{-i(q+k)a}\!} (1)

From differentiability and periodicity, the Schrödinger equation can be solved as the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\epsilon}^\epsilon -\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2}dx+\int_{-\epsilon}^\epsilon V_0\sum_{n=-\infty}^{\infty}\delta(x-na)\psi(x)dx=\int_{-\epsilon}^\epsilon E \psi(x)dx}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon\!} is small, approaching zero. In this case, the term on the right hand side can be taken to be 0. Thus,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{2m}(\frac{\partial\psi_r(\epsilon)}{\partial x}-\frac{\partial\psi_l(-\epsilon)}{\partial x})=-V_0\psi_l(0)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\epsilon\to 0}(\frac{\partial\psi_r(\epsilon)}{\partial x}-\frac{\partial\psi_l(-\epsilon)}{\partial x})=\frac{2mV_0}{\hbar^2}\psi_l(0)}

where,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\epsilon\to 0}\frac{\partial\psi_r(\epsilon)}{\partial x}=iq(A-B)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\epsilon\to 0}\frac{\partial\psi_l(-\epsilon)}{\partial x}=iq(Ae^{i(q-k)a}-Be^{-i(q+k)a})}

Evaluating further, the following condition is found:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iq(A-B-Ae^{i(q-k)a}+Be^{-i(q+k)a})=\frac{2mV_0}{\hbar^2}(A+B)} (2)

By simultaneously solving equation (1) and (2), the relationship between q and k is found to be:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(ka)=\cos(qa)+\frac{mV_0a}{\hbar^2}\frac{\sin(qa)}{qa}} (3)

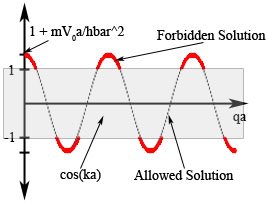
Where q is the energy band of the system, and k is the accessible energy band. By noting that the maximum value of the LHS is < the maximum value of the RHS of the relation above, it is clearly seen that there are some energy level that are not accessible as shown in Figure 3.

Figure 3. Graph of Eq.(3). Wave is representing the LHS function, gray box representing the range of RHS function. Red lines is the forbidden solution, black line is the allowed solution.

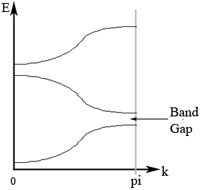
As k increases from 0 to , there will be many solutions. Focusing only to two of the allowed solutions, it is seen that as k increases, there will be two solutions (one solution gives increasing q value, the other solution gives decreasing q value). Using the fact that the energy of the system is , the dispersion relation (E vs. k) can be plotted as shown in Figure 4.

Figure 4. Energy vs k showing the existence of band gap for system of an electron under periodic potential.

Thus, in conjunction with Pauli exclusion principle, the single particle banspectrum such as the one we discussed here constitutes a simple description of band insulators and band metals.

Square Wave Potential

If we take a more general case, where the potential is also periodic and always finite. The potential can be expressed as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=\begin{cases} 0, na<x<na+c;\\ V_0, na+c<x<(n+1)a. \end{cases} }

Further, we assume that the eigenfunction is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_r=e^{ikx}u_k(x)\! }

Then this problem is converted to seeking for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(x)\!} in the region -b<x<c and connecting the wave function in different periods.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\right)\psi(x)=E_k\psi(x), 0<x<c}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V_0\right)\psi(x)=E_k\psi(x), -b<x<0}

Further we assume that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1^2=\frac{2mE_k}{\hbar^2}, k_2^2=\frac{2m(V_0-E_k)}{\hbar^2} }

Then we can get the equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(x)\!} :

${\frac {d^{2}u_{k}(x)}{x^{2}}}+2ik{\frac {du_{(}x)}{dx}}+(k_{1}^{2}-k^{2})u(x)=0,0<x<c$

${\frac {d^{2}u_{k}(x)}{x^{2}}}+2ik{\frac {du_{(}x)}{dx}}-(k_{2}^{2}+k^{2})u(x)=0,-b<x<0$

Solve for $u_{k}(x)\!$, we get:

$u_{k}(x)=A_{0}e^{i(k_{1}-k)x}+B_{0}e^{-i(k_{1}+k)x},0<x<c$

$u_{k}(x)=C_{0}e^{(k_{2}-ik)x}+D_{0}e^{-(k_{2}+ik)x},-b<x<o$

By the continuity of $\psi (x)\!$ and ${\frac {d\psi (x)}{dx}}$ at $x=0\!$:

$A_{0}+B_{0}=C_{0}+D_{0}\!$

$i(k_{1}-k)A_{0}-i(k_{1}+k)B_{0}=(k_{2}-ik)C_{0}-(k_{2}+ik)D_{0}\!$

By periodicity of $u_{k}(x)\!$, we get:

$u_{k}(x)=u_{k}(x+a)\!$

$C_{0}e^{(k_{2}-ik)x}+D_{0}e^{-(k_{2}+ik)x}=C_{1}e^{(k_{2}-ik)(x+a)}+D_{1}e^{-(k_{2}+ik)(x+a)}$

$C_{1}=C_{0}e^{-(k_{1}-ik)a}$

$D_{1}=D_{0}e^{(k_{2}+ik)a}$

By the continuity of $\psi (x)\!$ and ${\frac {d\psi (x)}{dx}}\!$ at $x=c\!$:

${\begin{aligned}A_{0}&e^{i(k_{1}-k)x}+B_{0}e^{-i(k_{2}+k)x}\\&=C_{1}e^{(k_{2}-ik)c}+D_{1}e^{-(k_{2}+ik)c}\\&=C_{0}e^{-(k_{2}-ik)b}+D_{0}e^{(k_{2}+ik)b}\end{aligned}}$

${\begin{aligned}i(k_{1}-k)&e^{i(k_{1}-k)c}A_{0}-i(k_{1}+k)e^{i(k_{1}+k)c}B_{0}\\=(k_{2}&-ik)e^{(k_{2}-ik)c}C_{1}-(k_{2}+ik)e^{-(k_{2}+ik)c}D_{1}\\=(k_{2}&-ik)e^{-(k_{2}-ik)b}C_{0}-(k_{2}+ik)e^{(k_{2}+ik)b}D_{0}\end{aligned}}$

Now, we get four linear equations of $A_{0},B_{0},C_{0}\!$ and $D_{0}\!$, to get the nontrivial solution, we have to make the determinant be zero:

${\frac {k_{2}^{2}-k_{1}^{2}}{2k_{1}k_{2}}}\sinh(k_{2}b)\sin(k_{1}c)+\cosh(k_{2}b)\cos(k_{1}c)=\cos(ka)$

This is the equation that the energy follows, where $k_{1}^{2}={\frac {2mE_{k}}{\hbar ^{2}}}\!$ and $k_{2}^{2}={\frac {2m(V_{0}-E_{k})}{\hbar ^{2}}}\!$.

If we take the limit $V_{0}\rightarrow 0\!$ and $b\rightarrow 0\!$ and maintain $V_{0}b\!$ finite, then we can obtain:

$k_{2}={\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E_{k})b^{2}}}\simeq {\sqrt {(V_{0}b){\frac {2mb}{\hbar ^{2}}}}}\ll 1$

$sinh(k_{2}b)\simeq k_{2}b$

$cosh(k_{2}b)\simeq 1$

Hence we get:

$\cos(ka)=\cos(k_{1}a)+{\frac {mV_{0}ab}{\hbar ^{2}}}{\frac {\sin(k_{1}a)}{k_{1}a}}$

This equation is the same as the equation we obtain on the condition of periodic delta potential. And we should be aware that $V_{0}b$ is finite and stand for the $V_{0}$ in the previous problem.

Problem

Find the energy spectrum for the case of an infinite series of Dirac delta function wells,

$V(x)=-V_{0}\sum _{n=-\infty }^{\infty }\delta (x-na).$

Note that, since the potential becomes negative, there will be negative-energy solutions.

Solution