Angular Momentum as a Generator of Rotations in 3D

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

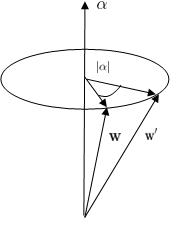
Let us consider an infinitesimal rotation described by a vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\alpha} \!} directed along the axis about which the rotation takes place and whose magnitude is the angle of the rotation. We then have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{w}' = \mathbf{w} + \mathbf{\alpha} \times \mathbf{w} = \mathbf{w} + \delta\mathbf{w} }

The changes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \mathbf w} (in the radial vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf w\!} of the particle) due to such a rotation is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \mathbf w=\mathbf{\alpha}\times \mathbf w}

so

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\left(\mathbf{w}+\mathbf{\delta} \mathbf{w}\right)=\left(1+\mathbf{\alpha}\cdot\left(\mathbf{w}\times\mathbf{\nabla}\right)\right)\psi\left(\mathbf{w}\right)}

The expression

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\mathbf{\alpha}\cdot(\mathbf{w}\times\mathbf{\nabla})}

is the operator of an infinitesimally small rotation. We recognize the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{w}\times\mathbf{\nabla}=\frac{i}{\hbar}\mathbf{L}}

Therefore, the infinitesimal rotation operator is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}_{inf}=1+\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}

This expression is only until the first order correction. The actual rotation operator is calculated by applying this operator N times where N goes to infinity. Doing so, we get the rotation operator for finite angle

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R} = e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}}

In this form, we recognize that angular momentum is the generator of rotation. And we can write the equation relating the initial vector before rotation with the transformed vector as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{w}'=e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}\mathbf{w} e^{-\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}}

This expression of the rotation operator is also valid when the rotation angle is not infinitesimal. What's more, this equation also implies that if we have a scalar instead of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{w}\!} , it would be invariant. We can also calculate the effect of the unitary operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}} on the states:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle r_0|e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}\mathbf{ \hat{\mathbf{r}}} e^{-\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}=\langle r_0|\hat{\mathbf{r'}}=r_0'\langle r_0|}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \psi'(r_0)=\langle r_0|\psi'\rangle=\langle r_0|e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}|\psi\rangle=\langle r_0'|\psi\rangle=\psi(r_0')}

This is the wavefunction evaluated at a rotated point.

A sample problem