Angular Momentum as a Generator of Rotations in 3D

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Let us consider an infinitesimal rotation described by a vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\alpha} \!} directed along the axis about which the rotation takes place and whose magnitude is the angle of the rotation. We then have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}' = \mathbf{r} + \mathbf{\alpha} \times \mathbf{r} = \mathbf{r} + \delta\mathbf{r}, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \mathbf{r}=\mathbf{\alpha}\times \mathbf{r}} is the change in the position vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}\!} of the particle due to such a rotation.

Let us now consider a function of position, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\mathbf{r}).} Substituting in the rotated coordinate and expanding to first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\mathbf{r},} we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\left(\mathbf{r}+\mathbf{\delta} \mathbf{r}\right)=\left [1+\mathbf{\alpha}\cdot\left(\mathbf{r}\times\mathbf{\nabla}\right)\right ]\psi\left(\mathbf{r}\right)}

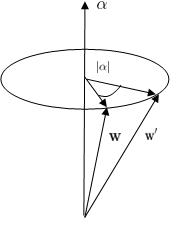
Figure 1: Illustration of the rotation considered here.

The expression,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\mathbf{\alpha}\cdot(\mathbf{r}\times\mathbf{\nabla}),}

may therefore be interpreted as an operator that performs an infinitesimally small rotation of position coordinates. Noticing that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}\times\mathbf{\nabla}=\frac{i}{\hbar}\hat{\mathbf{L}},}

we may write this infinitesimal rotation operator as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}_{inf}=1+\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}.}

Note that this expression only applies to infinitesimal rotations. We may construct a rotation operator for finite rotations, however, as follows. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\alpha}} be a finite rotation. Let us imagine performing this rotation as a sequence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\!} rotations by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathbf{\alpha}}{N},} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\!} is large. Each of these rotations may be treated as infinitesimal. The full rotation operator becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}(\mathbf{\alpha})=\left (1+\frac{i}{\hbar}\frac{\mathbf{\alpha}}{N}\cdot\hat{\mathbf{L}}\right )^N.}

If we now let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\rightarrow\infty,} we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}(\mathbf{\alpha})=e^{i\mathbf{\alpha}\cdot\hat{\mathbf{L}}/\hbar}.}

In this form, we recognize that angular momentum is a generator of rotations, similarly to how linear momentum generates translations.

The transformation rule for an operator is thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{O}'=e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}}\hat{O}e^{-\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}}.}

This expression is valid for any rotation. We see that, if the operator commutes with both position and momentum, then it will remain unchanged by a rotation.

We can also calculate the effect of the unitary operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}}} on the wave function, as follows. We first determine the effect of the operator on a position eigenstate:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \mathbf{r}_0|e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}}\mathbf{ \hat{\mathbf{r}}} e^{-\frac{i}{\hbar}\mathbf{\alpha}\cdot\hat{\mathbf{L}}}=\langle\mathbf{r}_0|\hat{\mathbf{r}}'=\mathbf{r}'_0\langle \mathbf{r}_0|}

As expected, the effect is to produce another position eigenstate, this one at the image of the rotation. The effect on the wavefunction is therefore as follows.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'(\mathbf{r}_0)=\langle \mathbf{r}_0|\psi'\rangle=\langle \mathbf{r}_0|e^{\frac{i}{\hbar}\mathbf{\alpha}\cdot\mathbf{L}}|\psi\rangle=\langle \mathbf{r}'_0|\psi\rangle=\psi(\mathbf{r}'_0)}

This is just the wave function evaluated at the rotated point.