Differential Cross Section and the Green's Function Formulation of Scattering

Quantum Mechanics A

Schrödinger Equation The most fundamental equation of quantum mechanics; given a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , it describes how a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

Physical Basis of Quantum Mechanics

Basic Concepts and Theory of Motion UV Catastrophe (Black-Body Radiation) Photoelectric Effect Stability of Matter Double Slit Experiment Stern-Gerlach Experiment The Principle of Complementarity The Correspondence Principle The Philosophy of Quantum Theory

Schrödinger Equation

Brief Derivation of Schrödinger Equation Relation Between the Wave Function and Probability Density Stationary States Heisenberg Uncertainty Principle Some Consequences of the Uncertainty Principle

Operators, Eigenfunctions, and Symmetry

Linear Vector Spaces and Operators Commutation Relations and Simultaneous Eigenvalues The Schrödinger Equation in Dirac Notation Transformations of Operators and Symmetry Time Evolution of Expectation Values and Ehrenfest's Theorem

Motion in One Dimension

One-Dimensional Bound States Oscillation Theorem The Dirac Delta Function Potential Scattering States, Transmission and Reflection Motion in a Periodic Potential Summary of One-Dimensional Systems

Discrete Eigenvalues and Bound States

Harmonic Oscillator Spectrum and Eigenstates Analytical Method for Solving the Simple Harmonic Oscillator Coherent States Charged Particles in an Electromagnetic Field WKB Approximation

Time Evolution and the Pictures of Quantum Mechanics

The Heisenberg Picture: Equations of Motion for Operators The Interaction Picture The Virial Theorem

Angular Momentum

Commutation Relations Angular Momentum as a Generator of Rotations in 3D Spherical Coordinates Eigenvalue Quantization Orbital Angular Momentum Eigenfunctions

Central Forces

General Formalism Free Particle in Spherical Coordinates Spherical Well Isotropic Harmonic Oscillator Hydrogen Atom WKB in Spherical Coordinates

The Path Integral Formulation of Quantum Mechanics

Feynman Path Integrals The Free-Particle Propagator Propagator for the Harmonic Oscillator

Continuous Eigenvalues and Collision Theory

Differential Cross Section and the Green's Function Formulation of Scattering Central Potential Scattering and Phase Shifts Coulomb Potential Scattering

Much of what we know about forces and interactions in atoms and nuclei has been learned from scattering experiments, in which say atoms in the target are bombarded with beams of particles. These particles are scattered by the target atoms and then detected as a function of a scattering angle and energy. From a theoretical point of view, we are now concerned with the continuous part of the energy spectrum. We are free to choose the value of the incident particle energy and by a proper choice of the zero of energy, this corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E>0\!} an to eigenfunctions of the unbound states. Before, when we were studying the bound states, the focus was on the discrete energy eigenvalues which allow a direct comparison of theory and experiments. In the continuous part of the spectrum, as it comes into play in scattering, the energy is given by the incident beam, and intensities are the object of measurement and prediction. These being the measures of the likelihood of finding a particle at certain places, are of course related to the eigenfunctions, rather than eigenvalues. Relating observed intensities to calculated wave functions is the first problem in scattering theory.

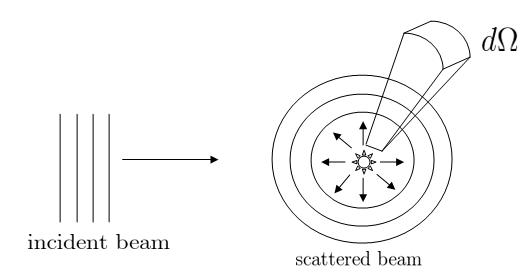
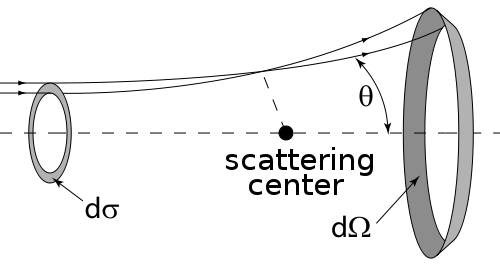
Figure 1: Collimated homogeneous beam of monoenergetic particles, long wavepacket which is approximately a planewave, but strictly does not extend to infinity in all directions, is incident on a target and subsequently scattered into the detector subtending a solid angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\Omega\!} . The detector is assumed to be far away from the scattering center.

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_0\!} is the number of particles incident from the left per unit area per time and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\theta,\phi)d\Omega\!} the number of those scattered into the cone per time and if the density of particles in the incident beam is so small such that we can neglect the interaction of the particles with each other and consider their collisions like independent events then this two quantities are proportional to each other. With these considerations the differential cross section is defined as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=\frac{I(\theta,\phi)}{I_0}}

There exist two different types of scattering; elastic scattering, where the incident energy is equal to the detected energy and inelastic scattering which arises from lattice vibrations within the sample. For inelastic scattering, one would need to tune the detector detect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E+dE\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dE\!} results from the quantum lattice vibrations. For simplification purposes, we will only be discussing elastic scattering.

To describe this scattering, start with the stationary Schrödinger equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\hbar^2}{2m}\nabla^2+V(\mathbf r)\right)\psi(\mathbf r)=E\psi(\mathbf r)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow (\nabla^2+k^2)\psi(\mathbf r)=\frac{2mV(\mathbf r)}{\hbar^2}\psi(\mathbf r)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\frac{\hbar^2k^2}{2m}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\mathbf r)\!} will be assumed to be finite in a limited region of space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r<d\!} . This is called the range of the force, e.g. nuclear forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\sim10^{-15}m\!} and atomic forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\sim10^{-10}m\!} . Outside this range of forces, the particles move essentially freely. Our problem consists in finding those solutions of the above differential equation which can be written as a superposition of an incoming and an outgoing scattered waves. We found such solutions by writing the Schrödinger differential equation as an integral equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k(\mathbf r)=\psi_k^{(0)}( \mathbf r ) +\int d^3r'G_k(\mathbf r,\mathbf r')\frac{2m}{\hbar^2}V(\mathbf r')\psi_k(\mathbf r')}

where the Green's function satisfies

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2)G_k(\mathbf{r},\mathbf{r'})=\delta(\mathbf{r}-\mathbf{r'})}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2 )\psi^{(0)}_k(\mathbf{r})=0}

and the solution is chosen such that the second term in the above wave function corresponds to an outgoing wave. Then, the outgoing Green's function can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{k}(\mathbf r,\mathbf r')=-\frac{1}{4\pi}\frac{e^{ik|\mathbf{r}-\mathbf{r}'|}}{|\mathbf{r}-\mathbf{r}'|}.}

The full wave function solution will become an integral equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi _{k}(\mathbf{r})=\psi _{k}^{(0)}(\mathbf{r})-\frac{m}{2\pi \hbar ^{2}}\int {d^{3}r}' \text{ }\frac{e^{ik\left|\mathbf{r}-\mathbf{r}' \right |}}{\left |{\mathbf{r-r'}} \right |}V(\mathbf{r'})\psi _{k}(\mathbf{r'}),}

where the first term represents incident plane waves and the second term represents scattered waves.

The detector is located far away from the scattering potential and we need to discuss the asymptotic behaviour in the limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\to\infty\!} . In this limit,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \left| \mathbf{r}-\mathbf{r}'\right| \sim kr - k\mathbf{r}' \cdot \mathbf{\hat{r}} = kr - \mathbf{k}' \cdot \mathbf{r}', }

where the wave vector, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}' = k \mathbf{\hat{r}} } , is seen far from the scattering potential.

Therefore we can write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \lim_{r \to \infty} \psi_k(\mathbf{r}) &= \psi_k^{(0)}(\mathbf{r}) -\frac{m}{2\pi\hbar^2 }\int d^3 r'e^ {-i\mathbf{k}'\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'})\frac{e^{ikr}}{r} \\ &= \psi_k^{(0)}(\mathbf{r})+f_k(\theta,\phi)\frac{e^{ikr}}{r}, \end{align} }

where the scattering amplitude

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta,\phi)=-\frac{m}{2\pi\hbar^2 }\int d^3 r'e^{-i\mathbf{k}'\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'}) }

and the angles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} are the angles between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\hat{r}}\!} (the vector defining the detector) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}\!} (the vector defining the in the incoming waves).

Now the differential cross section is written through the ratio of the (outgoing) radial current density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_r\!} and the incident current density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{inc}\!} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=\frac{j_r r^2}{j_{inc}}}

The radial current is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_r=\frac{\hbar}{2mi}\left(\psi_{sc}^*\frac{\partial \psi_{sc}}{\partial r}-\psi_{sc}\frac{\partial \psi_{sc}^*}{\partial r}\right)=\frac{\hbar k}{mr^2}|f_k(\theta,\phi)|^2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{d\sigma}{d\Omega}=|f_k(\theta,\phi)|^2}

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\mathbf{r})} that is small, the full wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_k(\mathbf{r})\rangle } can be obtained by substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_k(\mathbf{r})\rangle } into RHS of the integral equation iteratively as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi_k(\mathbf{r}) =\psi_k^{(0)}(\mathbf{r}) + \left(\frac{2m}{\hbar^2}\right) \int d^3r'G_k(\mathbf r,\mathbf r')V(\mathbf{r'})\psi_k^{(0)}(\mathbf{r'}) \\ + \left(\frac{2m}{\hbar^2}\right)^{2} \int d^3r' \int d^3r'' G_k(\mathbf r,\mathbf r') & V(\mathbf{r'}) G_k(\mathbf r',\mathbf r'')V(\mathbf{r''}) \psi_k^{(0)}(\mathbf{r''})+... \end{align} }

In 1st Born approximation, we keep only one Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\mathbf{r})} term. For large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k(\mathbf{r})\approx\psi_k^{(0)}(\mathbf{r}) -\frac{m}{2\pi\hbar^2 }\int d^3r'e^{-i\mathbf{k}'\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k^{(0)}(\mathbf{r'})\frac{e^{ikr}}{r}}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta,\phi)=-\frac{m}{2\pi\hbar^2 }\int d^3r'e^{-i\mathbf{k}'\cdot\mathbf{r'}}V(\mathbf{r'})e^{i\mathbf{k}\cdot \mathbf r'}=-\left(\frac{m}{2\pi\hbar^2}\right)|\langle\mathbf k_{sc}|V|\mathbf k_{inc}\rangle|}

For a central-force potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) } , the Born scattering amplitude reduces to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta) = \frac{-m}{2 \pi \hbar^2}\int d^3r'V(r') e^{-i\mathbf q \mathbf r'} }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf q = \mathbf k' - \mathbf k }

is known as the momentum transfer (in units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar } ). Keep in mind that k' is the wave vector pointing in the incident direction and k is in the scattered direction.

For spherically symetric potintials Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\mathbf r) = V(r) } , so that all the angular dependence is carried by q. The integral over the solid angle is easily carried out and yields the following result:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{born}(\theta) = \frac{-2m}{\hbar^2} \int_0^\infin dr' V(r') \frac{\sin(qr')}{qr'} {r'}^2 }

Here we have denoted the scattering angle between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } and $k'$ by $\theta$ , and note that $k'=k$ for elastic scattering, so that

$q=2k\sin \left({\frac {\theta }{2}}\right)$.

As an example, consider the screened Coulomb potential

$V(r)=V_{0}{\frac {e^{-\alpha r}}{\alpha r}}.$

In the Born approximation , after a simple integration over the angles, we find

${\begin{aligned}f_{born}(\theta )&={\frac {-2m}{\hbar ^{2}}}V_{0}\int _{0}^{\infty }dr'{r'}^{2}{\frac {e^{-\alpha r}}{\alpha r'}}{\frac {\sin(qr')}{qr'}}\\&={\frac {-2m}{\alpha \hbar ^{2}}}V_{0}{\frac {1}{q^{2}+\alpha ^{2}}}\\&={\frac {-2mV_{0}}{\hbar ^{2}\alpha }}{\frac {1}{4k^{2}\sin ^{2}(\theta /2)+\alpha ^{2}}}\end{aligned}}$

The differential scattering cross section is obtained simply by taking the square of this amplitude.

${\frac {d\sigma }{d\Omega }}=\left|{\frac {-2mV_{0}}{\hbar ^{2}\alpha }}{\frac {1}{4k^{2}\sin ^{2}(\theta /2)+\alpha ^{2}}}\right|^{2}$

The Coulomb potential between two charges $q_{1}$ and $q_{2}$ is a limiting case of the potential

$V(r)=V_{0}{\frac {e^{-\alpha r}}{\alpha r}}$

for $\alpha \rightarrow 0\!$ and $V_{0}\rightarrow 0\!$ with ${\frac {V_{0}}{\alpha }}=q_{1}q_{2}\!$. Thus, in the Born approximation,

${\begin{aligned}{\frac {d\sigma }{d\Omega }}&={\frac {m^{2}{q_{1}}^{2}{q_{2}}^{2}}{4p^{4}\sin ^{4}({\frac {\theta }{2}})}}\\&={\frac {{q_{1}}^{2}{q_{2}}^{2}}{16E^{2}\sin ^{4}({\frac {\theta }{2}})}}\end{aligned}}$

Note, that the exact Coulomb scattering amplitude differs from the Born amplitude by a phase factor.