Feynman Path Integrals
The path integral formulation of quantum mechanics was developed in 1948 by Richard Feynman. The path integral formulation is a description of quantum theory that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique trajectory for a system with a sum, or functional integral, over an infinity of possible trajectories to compute a quantum amplitude.
The classical path is the path that minimizes the action.
This formulation has proved crucial to the subsequent development of theoretical physics, since it is apparently symmetric between time and space. Unlike previous methods, the path-integral offers us an easily method by which we may change coordinates between very different canonical descriptions of the same quantum system.
For simplicity, the formalism is developed here in one dimension.
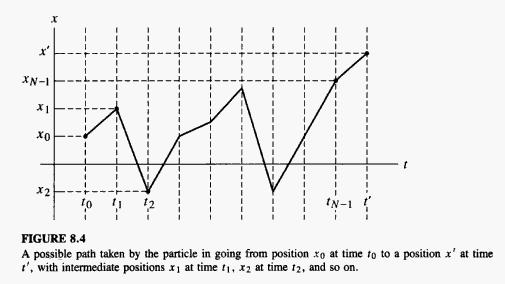
In the path integral formalism, we start by writing the amplitude for a particle at position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i\!} at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_i\!} to move to a position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_f\!} at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_f\!} as a path integral. This path integral is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(x_f,t_f;x_i,t_i)=\langle x_f,t_f|\hat{U}(t_f,t_i)|x_i,t_i\rangle=\int D x(t')\,e^{iS[x(t')]/\hbar}, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[x(t)]\!} is the action for the the path Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t')\!} and the integral is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int D x(t')=\lim_{N\to\infty}\left (\frac{m}{2\pi i\hbar\,\delta t}\right )^{N/2}\left (\prod_{j=1}^{N-1}\int_{-\infty}^{\infty} dx_j\right ),}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\!} is a number of "slices" of length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\!} that we divide the time axis up into. Essentially, we define the path integral as a limit of an integral over all possible values of the particle's intermediate positions on its path from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x.\!}
The action is given by the time integral of the Lagrangian, just as in classical mechanics: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[x(t')]=\int_{t_i}^{t_f} dt' \mathcal{L}[x(t'),\dot{x}(t'),t'], }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}[x(t'),\dot{x}(t'),t']=\tfrac{1}{2}m\dot{x}^2(t')-V(x(t'),t') }
is the Lagrangian.
Our choice of notation for this path integral, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(x_f,t_f;x_i,t_i),\!} is motivated by the fact that it serves as a "kernel" for an integral giving the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t_f)\!} in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x,t).\!} This integral is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t_f)=\int_{-\infty}^{\infty} dx\,K(x_f,t_f;x,t)\Psi(x,t).}
Obtaining the Schrödinger Equation From the Path Integral Formalism
As a justification of this method, we will show that it reproduces the Schrödinger equation. The following derivation follows that of Feynman. Let us begin by assuming that the elapsed time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\!} is so small, that we may approximate the path integral with a single "time slice" of that length. In this case, the kernel is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{iS/\hbar},} and the action is just its average over the time interval times is length:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\frac{m(x_f-x)^2}{2\delta t}-V[\tfrac{1}{2}(x_f+x),t]\,\delta t}
The kernel now becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(x_f,t_f;x,t)=\sqrt{\frac{m}{2\pi i\hbar\,\delta t}}\exp\left [\frac{im(x_f-x)^2}{2\hbar\,\delta t}\right ]\exp\left [-\frac{i}{\hbar}V[\tfrac{1}{2}(x_f+x),t]\,\delta t\right ],}
so that the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t_f)=\Psi(x_f,t+\delta t)\!} is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\sqrt{\frac{m}{2\pi i\hbar\,\delta t}}\int_{-\infty}^{\infty} dx\,\exp\left [\frac{im(x_f-x)^2}{2\hbar\,\delta t}\right ]\exp\left [-\frac{i}{\hbar}V[\tfrac{1}{2}(x_f+x),t]\,\delta t\right ]\Psi(x,t).}
Now we introduce the variable, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=x_f-x,\!} so that the integral becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\sqrt{\frac{m}{2\pi i\hbar\,\delta t}}\int_{-\infty}^{\infty} d\xi\,\exp\left (\frac{im\xi^2}{2\hbar\,\delta t}\right )\exp\left [-\frac{i}{\hbar}V(x_f-\tfrac{1}{2}\xi,t)\,\delta t\right ]\Psi(x_f-\xi,t).}
We now expand the wave function in the integral in powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} up to second order and the factor involving the potential in powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\!} up to first order. We also drop all dependence of the potential on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi.\!} The result of this is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\sqrt{\frac{m}{2\pi i\hbar\,\delta t}}\int_{-\infty}^{\infty} d\xi\,\exp\left (\frac{im\xi^2}{2\hbar\,\delta t}\right )\left [1-\frac{i}{\hbar}V(x_f,t)\,\delta t\right ]\left [\Psi(x_f,t)-\frac{\partial\Psi(x_f,t)}{\partial x_f}\xi+\tfrac{1}{2}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}\xi^2\right ].}
The problem has been reduced to the evaluation of Gaussian integrals. Using the formulas,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty}dx\,e^{-ax^2}=\sqrt{\frac{\pi}{a}},}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty}dx\,xe^{-ax^2}=0,}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty}dx\,x^2e^{-ax^2}=\frac{1}{2a}\sqrt{\frac{\pi}{a}},}
we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\left [1-\frac{i}{\hbar}V(x_f,t)\,\delta t\right ]\left [\Psi(x_f,t)+\frac{i\hbar}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}\,\delta t\right ].}
We now multiply out the right-hand side and retain only terms that are first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t.\!} This gives us
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x_f,t+\delta t)=\Psi(x_f,t)+\frac{i\hbar}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}\,\delta t-\frac{i}{\hbar}V(x_f,t)\Psi(x_f,t)\,\delta t.}
Rearranging, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\Psi(x_f,t+\delta t)-\Psi(x_f,t)}{\delta t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi(x_f,t)}{\partial x_f^2}+V(x_f,t)\Psi(x_f,t).}
Finally, taking the limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta t\to 0,\!} and renaming Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_f\!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,\!} we finally arrive at the familiar Schrödinger equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial\Psi(x,t)}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi(x,t)}{\partial x^2}+V(x,t)\Psi(x,t).}
As a final remark, we note that using the Feynman path integral formulation of quantum mechanics is more complex than solving the Schrödinger equation to obtain the dynamics of a quantum particle. Why, then, is this formulation mentioned in textbooks and where it may be useful?
For a single-particle problem, using the Schrödinger equation is definitely easier. However, to study a many-body system, solving the Schrödinger equation can be rather complicated and messy (let's just say sometimes impossible), while the Feynman path integral is a good tool for dealing with many-body problems by defining the field operators. More importantly, the generalization of quantum mechanics to relativistic problems can be done in terms of field operators via the Feynman path integral formulation. These applications, while of great interest, are beyond the scope of the present work.